1 .Сила взаимодействия двух отрицательных точечных зарядов, находящихся на расстоянии R друг от друга, равна F . Знаки зарядов обеих частиц изменили на противоположные. Чтобы сила взаимодействия F не изменилась, расстояние между зарядами надо …
уменьшить в 2 раза
оставить без изменения
увеличить в 4 раза
уменьшить в
увеличить в 2 раза
Решение:
Оставить без изменения
2.
На рисунке показано направление вектора напряженности результирующего электрического поля точечных зарядов q 1 и q 2 в точке А. 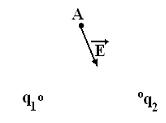
При этом для зарядов и справедливо соотношение…
, ; , ; , ; ,
Решение:
Построить все варианты. , - да.
3.
Электростатическое поле создано двумя точечными зарядами: и . Отношение потенциала поля, созданного вторым зарядом в точке А, к потенциалу результирующего поля в этой точке равно … 4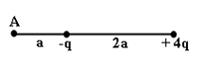
Решение:
(Коэффициенты при делении сокращаются)
4.
Электростатическое поле создано системой точечных зарядов.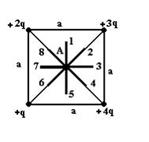
Вектор напряженности поля в точке А ориентирован в направлении …7
Решение:
![]() – векторы напряженности полей, создаваемых точечными зарядами Сделать рисунок.
– векторы напряженности полей, создаваемых точечными зарядами Сделать рисунок.
5 . Электростатическое поле создано системой точечных зарядов , и .
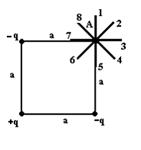
Градиент потенциала поля в точке А ориентирован в направлении …2
Решение:
Диагональ равна . Напряженность от зарядов направлена в т. А по 6 и равна по величине . Напряженность от заряда в т.А направлена по 2 и по величине равна . Так как 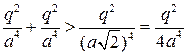 , то напряженность в т.А направлена по 6. Следовательно по 2. (для простоты опущены коэф.-ты )
, то напряженность в т.А направлена по 6. Следовательно по 2. (для простоты опущены коэф.-ты )
6
.Вектор напряженности электростатического поля в точке А
между эквипотенциальными поверхностями В и В имеет направление …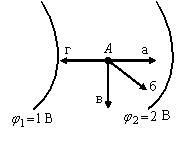
Решение:
Т.к. вектор , то вектор всегда направлен в сторону уменьшения перпендикулярно эквипотенциальным поверхностям, т.е. по направлению г.
7
. Электростатическое поле создано системой точечных зарядов.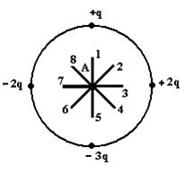
Вектор напряженности поля в точке А ориентирован в направлении …6
Решение:
Согласно принципу суперпозиции полей напряженность в точке А равна: , где ![]() – векторы напряженности полей, создаваемых точечными зарядами , , , в рассматриваемой точке соответственно. На рисунке показаны направления этих векторов.
– векторы напряженности полей, создаваемых точечными зарядами , , , в рассматриваемой точке соответственно. На рисунке показаны направления этих векторов. 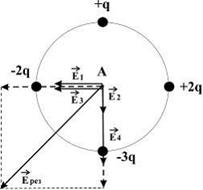
. Учитывая величины зарядов и то, что точка А одинаково удалена от каждого заряда, можно сделать вывод, что образует диагональ квадрата со стороной 2Е
1 . Таким образом, вектор напряженности поля в точке А ориентирован в направлении 6.
8
. В некоторой области пространства создано электростатическое поле, потенциал которого описывается функцией . Вектор напряженности электрического поля в точке пространства, показанной на рисунке, будет иметь направление …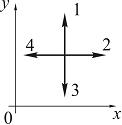 Решение:
Решение:
![]() , , , . Следовательно
, , , . Следовательно ![]() , т.е. вектор напряженности направлен по 4.
, т.е. вектор напряженности направлен по 4.
9
. Электростатическое поле образовано двумя параллельными бесконечными плоскостями, заряженными разноименными зарядами с одинаковой по величине поверхностной плотностью заряда. Расстояние между плоскостями равно d
.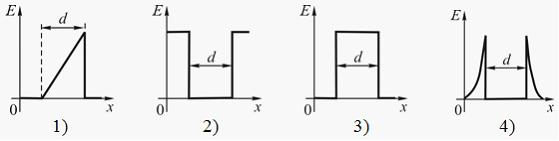
Распределение напряженности Е
такого поля вдоль оси х
, перпендикулярной плоскостям, правильно показано на рисунке …
Решение:
Электростатическое поле, в этом случае, сосредоточено между плоскостями и является однородным. Напряженность поля постоянна и не зависит от х, а вне – равна нулю. Таким образом, правильный график на рисунке 3.
10.
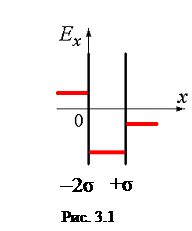 Электрическое поле создано двумя параллельными плоскостями, заряженными с поверхностными плотностями –
2σ и +σ. На рис. 3.1 показана качественная зависимость проекции напряженности Е х
от координаты х
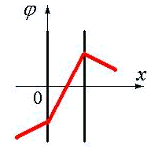
вне пластин и между пластинами. Правильно отражает характер изменения потенциала φ этого поля график
Электрическое поле создано двумя параллельными плоскостями, заряженными с поверхностными плотностями –
2σ и +σ. На рис. 3.1 показана качественная зависимость проекции напряженности Е х
от координаты х
вне пластин и между пластинами. Правильно отражает характер изменения потенциала φ этого поля график
| 1) на рис. 3.2 | 2) на рис. 3.3 |
| 3) на рис. 3.4 | 4) на рис. 3.5 |
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
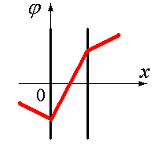 Рис. 3.4 |
|
Цель работы: экспериментальное изучение свойств электростатического поля и построение графика расположения силовых линий при помощи кривых равного потенциала.
Приборы и оборудование: электролитическая ванна, осциллограф, вольтметр, потенциометр, ключ, электроды различной конфигурации.
Теоретические сведения
Электрическое поле - вид материи, осуществляющий взаимодействие неподвижных электрических зарядов. Каждый заряд имеет свое электростатическое поле, которое в каждой точке пространства характеризуется вектором напряженности и электростатическим потенциалом φ.
Напряженностью
электростатического поля в точке
называется векторная физическая
величина, численно равная отношению
силы
 , действующей на пробный зарядq o ,
к величине этого заряда, помещенного в
данную точку поля:
, действующей на пробный зарядq o ,
к величине этого заряда, помещенного в
данную точку поля:
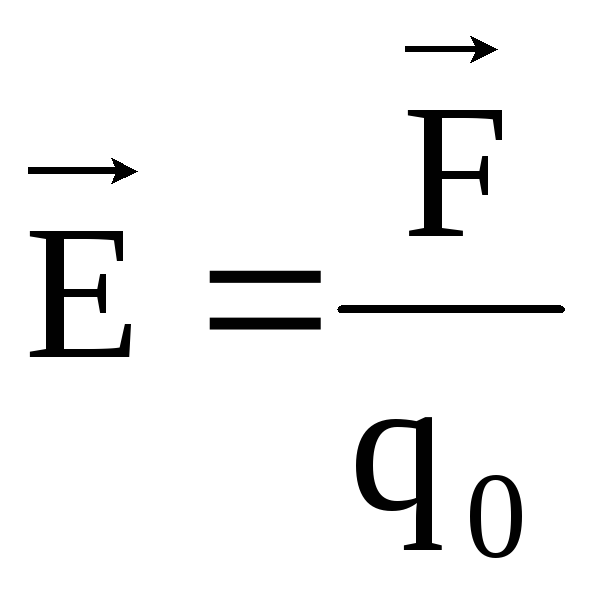 .
(1)
.
(1)
Если
пробный заряд q o =+l,
то
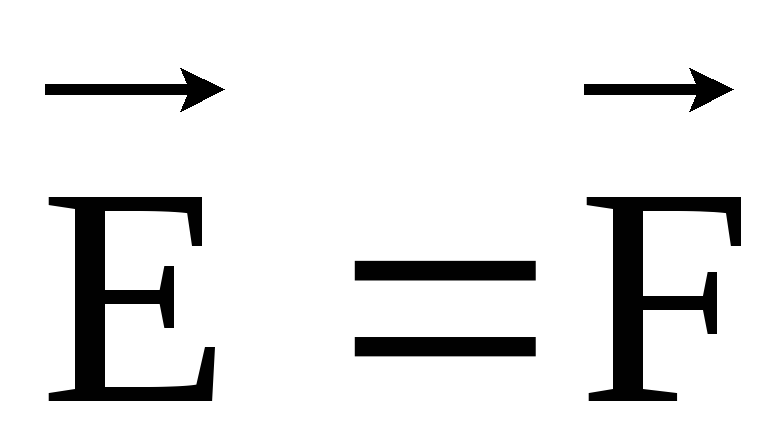 .А
потому вектор напряженности
электростатического
поля равен силе, действующей на единичный
пробный заряд.
.А
потому вектор напряженности
электростатического
поля равен силе, действующей на единичный
пробный заряд.
Направление
вектора
 совпадает с направлением силы. Из формулы
(1) следует,
что единица напряженности электрического
поля - ньютон на кулон (Н/Кл);
1Н/Кл - напряженность такого поля, которое
на точечный заряд в 1Кл действует с силой
в 1Н.
совпадает с направлением силы. Из формулы
(1) следует,
что единица напряженности электрического
поля - ньютон на кулон (Н/Кл);
1Н/Кл - напряженность такого поля, которое
на точечный заряд в 1Кл действует с силой
в 1Н.
Вектор
 во всех точках поля направлен радиально
от заряда, если он положителен,
и радиально к заряду, если он отрицателен
(рис. 1).
во всех точках поля направлен радиально
от заряда, если он положителен,
и радиально к заряду, если он отрицателен
(рис. 1).

Электростатическое поле можно изобразить силовыми линиями. Силовой линией, или линией напряженности электростатического поля называется линия, в каждой точке которой вектор напряженности направлен по касательной (рис. 2),
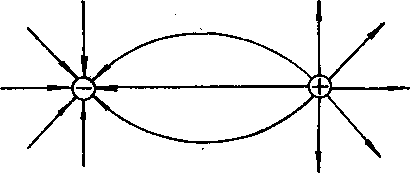
Силовые линии всегда начинаются на поверхности положительно заряженных тел, а заканчиваются на поверхности отрицательно заряженных тел или уходят в бесконечность.
Если поле создано уединенным точечным зарядом q, то работа, совершаемая полем при перемещении пробного заряда q o из положения 1 в положение 2 (рис. 3), не зависит от траектории перемещения:
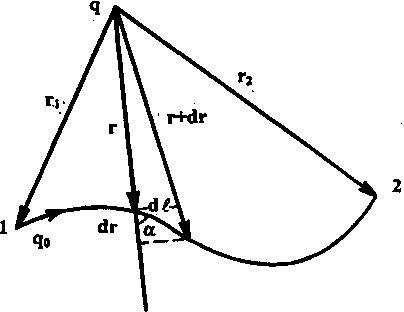
Из выражения (2) видно, что работа определяется только положением начальной 1 и конечной 2 точек. Силы, работа которых не зависит от траектории движения, называются консервативными. В этом случае электрическое поле является потенциальным, а формула принимает вид А 1,2 =-ΔW p . Знак «минус» означает, что положительная работа совершается самим полем за счет уменьшения энергии
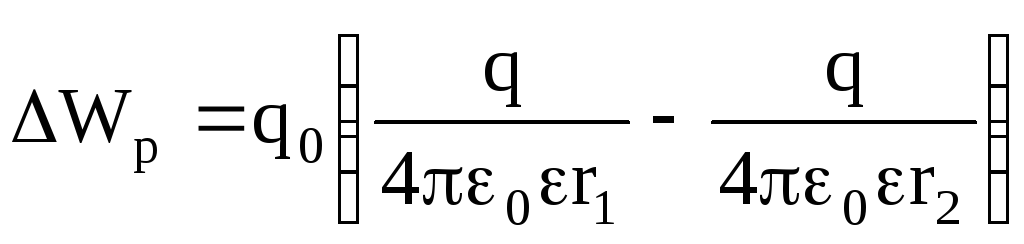 .
(3)
.
(3)
Значит, потенциальная энергия двух точечных зарядов, находящихся на расстоянии r,
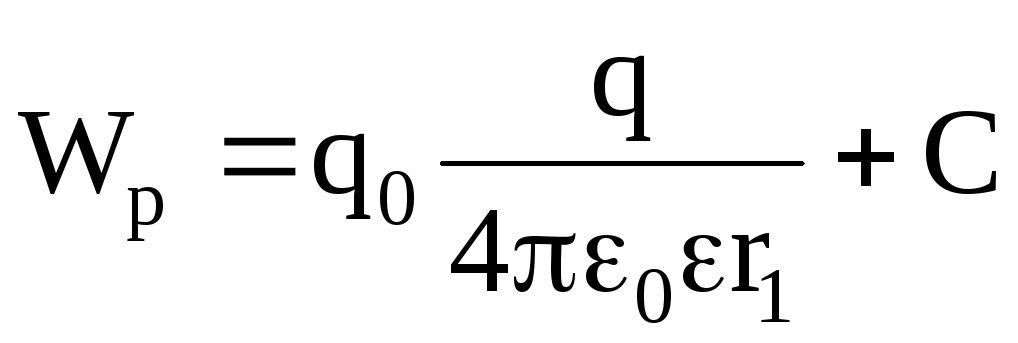 (4)
(4)
Величину
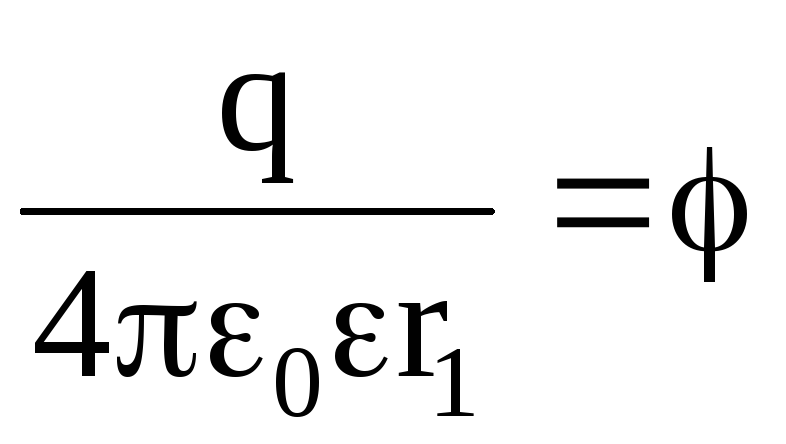 называют
потенциалом поля точечного заряда.
Тогда 4яе 0 ег
называют
потенциалом поля точечного заряда.
Тогда 4яе 0 ег
формула (2) принимает вид
А 1,2 =q 0 (φ 1 -φ 2). (5)
Подставив
в (4) значения q o =+l
и С=0, получим
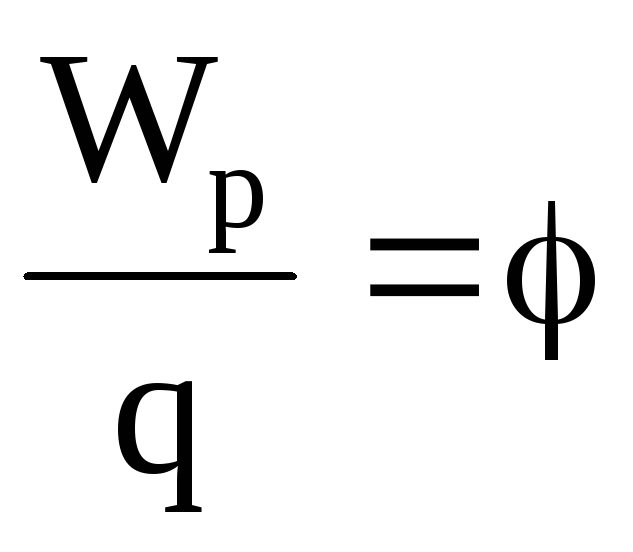 .
Потенциал некоторой
точки поля есть физическая величина,
численно равная потенциальной энергии
единичного положительного заряда,
помещенного в эту точку. Потенциал
–
энергетическая
характеристика поля.
.
Потенциал некоторой
точки поля есть физическая величина,
численно равная потенциальной энергии
единичного положительного заряда,
помещенного в эту точку. Потенциал
–
энергетическая
характеристика поля.
Пользуясь формулами (2), (4) и (5), уравнение работы, совершаемой электрическими силами при перемещении заряда q 0 из точки 1 в точку 2, можно записать в виде
A 1,2 =W p 1 -W p 2 =q 0 (φ 1 -φ 2) . (6)
Работа при перемещении точечного заряда равна произведению этого заряда на разность потенциалов в начальной и конечной точках пути.
Если точка 2 лежит в бесконечности, то потенциальная энергия заряда q o в ней равна нулю (W p 2 =0), а следовательно, и потенциал поля также равен нулю (φ 2 = 0). Тогда согласно (6)
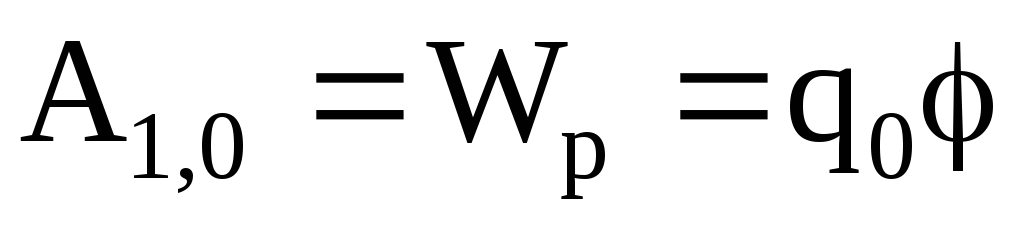 . (7)
. (7)
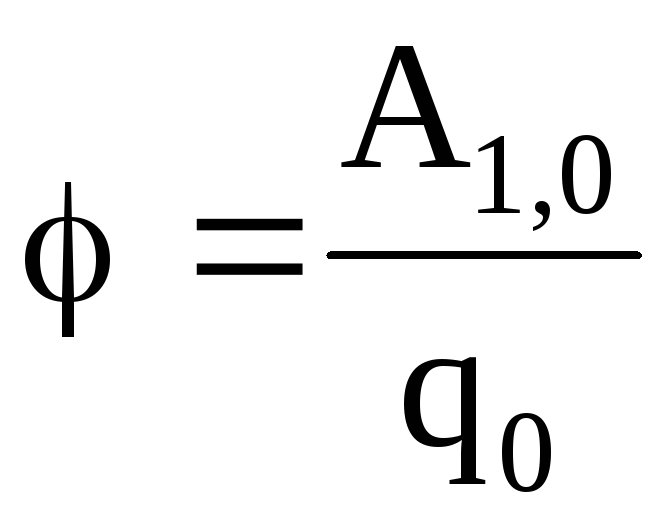 . (8)
. (8)
Поэтому потенциал данной точки поля можно определить как физическую величину, численно равную работе, совершаемой электрическими силами при перемещении единичного положительного заряда из данной точки в бесконечность.
В системе СИ за единицу потенциала принят вольт (В), т.е. потенциал такой точки поля, для перемещения в которую из бесконечности заряда, равного 1 Кл, необходимо совершить работу в 1 Дж: 1 Дж=1Кл·В. Отсюда 1 В=Дж/Кл. Геометрическое место точек поля, обладающих равными потенциалами, называется эквипотенциальной поверхностью. Работа при перемещении заряда по ней равна нулю. Этот вывод вытекает из определения работы поля при перемещении в нем заряда: А=q 0 (φ 1 -φ 2), т.к. φ 1 =φ 2 .
Силовые
линии всегда нормальны к эквипотенциальным
поверхностям. Докажем
это методом от противного. Пусть Q
- часть этой поверхности (рис. 4), В и С -
ее точки, а вектор
 не перпендикулярен Q.
Но тогда должна быть E t
-
не перпендикулярен Q.
Но тогда должна быть E t
-
касательная
составляющая вектора
 ,
параллельная поверхности Q.
Значит, работа
на участке ВС отлична от нуля, что
невозможно. Следовательно, вектор
,
параллельная поверхности Q.
Значит, работа
на участке ВС отлична от нуля, что
невозможно. Следовательно, вектор
 перпендикулярен эквипотенциальной
поверхности.
перпендикулярен эквипотенциальной
поверхности.
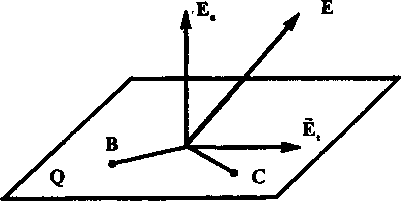
Определим связь между напряженностью и потенциалом. С одной стороны, работа при перемещении заряда q 0 с эквипотенциальной поверхности, имеющей потенциал φ, на расположенную поблизости эквипотенциальную поверхность с потенциалом φ + Δφ по нормали к ней(на расстояние Δn) рассчитывается по формуле ΔА = q 0 En (рис. 5).
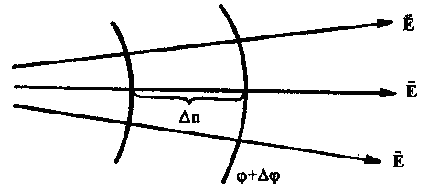
Напряженность
поля
 при бесконечно малом перемещении можно
считать
постоянной. С другой стороны, величину
этой работы можно вычислить по формуле
(5). Таким образом,
при бесконечно малом перемещении можно
считать
постоянной. С другой стороны, величину
этой работы можно вычислить по формуле
(5). Таким образом,
Откуда
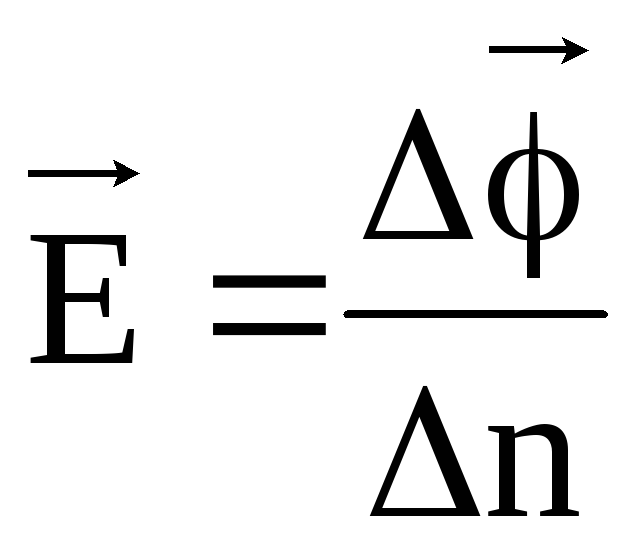 , (9)
, (9)
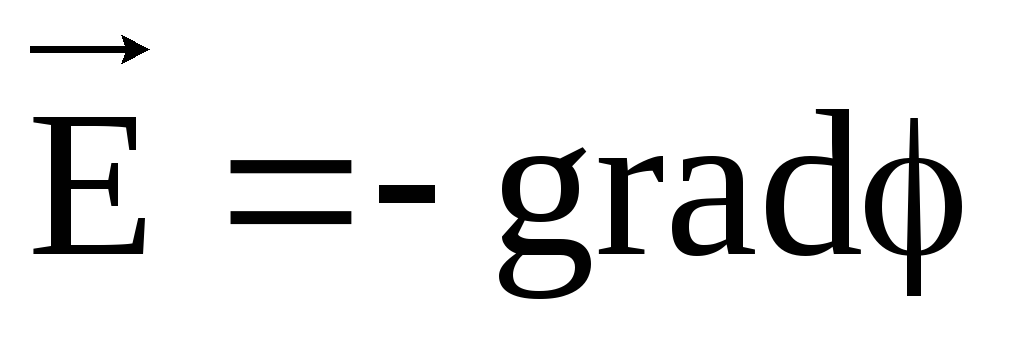 .
.
Знак «минус» указывает на то, что вектор напряженности направлен в сторону убывания потенциала.
Из формулы (9) следует, что единица напряженности 1Н/Кл=1В/м, где В (вольт) - единица потенциала электрического поля.
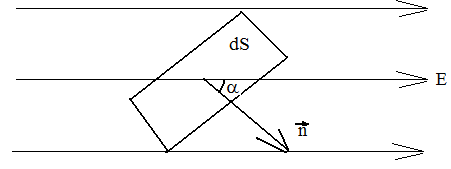
Число
силовых линий пронизывающих элементарную
площадку dS,
нормаль n
которой образует с направление вектора
Е угол ,
называется потоком напряженности
электрического поля через эту площадку
 ,
(рис. 7)
,
(рис. 7)
Для произвольной замкнутой поверхности
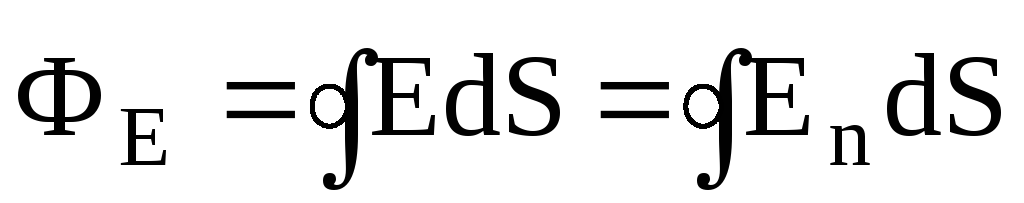 ,
(10)
,
(10)
где Е n =Ecos.
Поток не зависит от формы и размеров замкнутой поверхности, места нахождения заряда внутри охватываемого этой поверхностью объема.
Поток вектора напряженности, пронизывающий любую замкнутую поверхность, окружающую электрические заряды, равен алгебраической сумме зарядов внутри этой поверхности деленной на 0
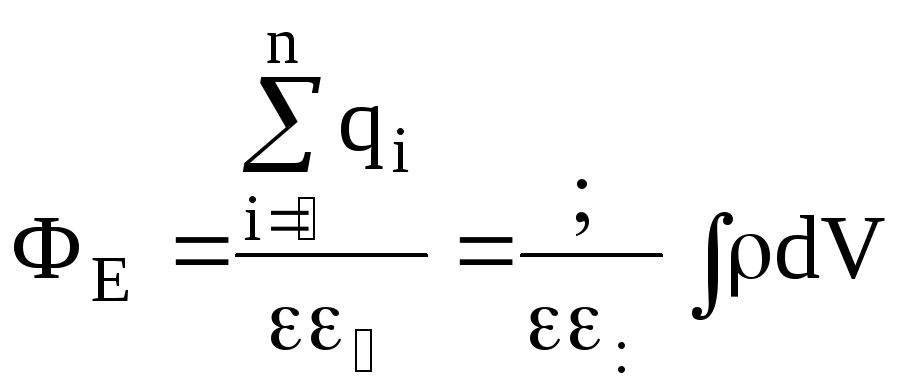 ,
(11)
,
(11)
где
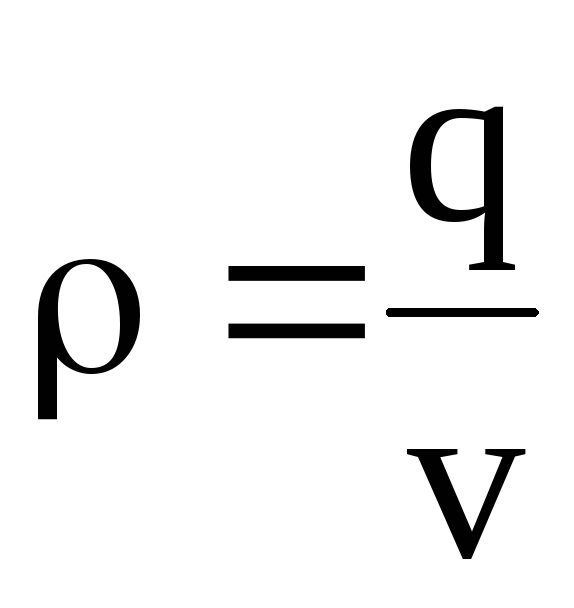 .
.
Это положение называется теоремой Остроградского-Гаусса
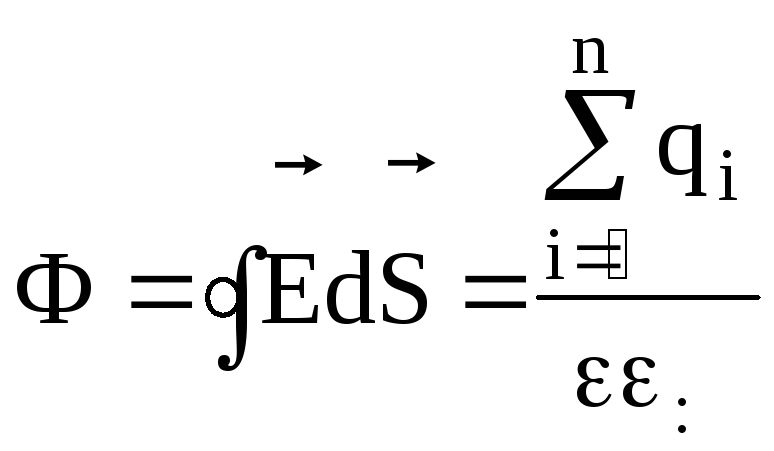 .
(12)
.
(12)
С помощью теоремы Остроградского-Гаусса сложно определять напряженность полей, создаваемых заряженными телами различной формы.
Напряженность поля создаваемого равномерно заряженной бесконечной плоскостью
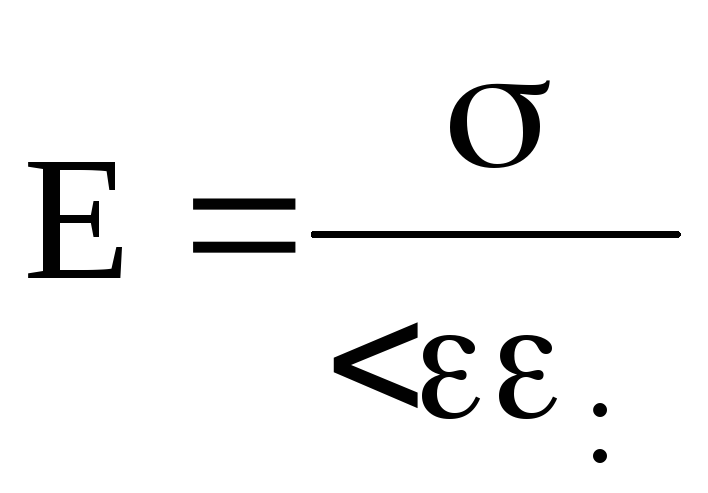 ,
(13)
,
(13)
где
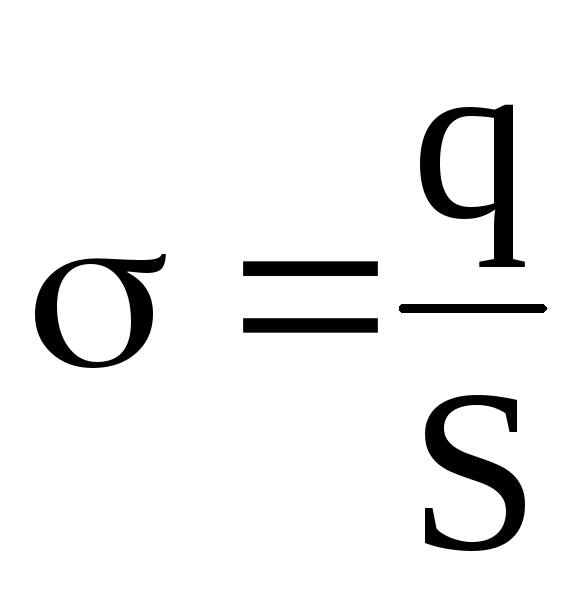 .
.
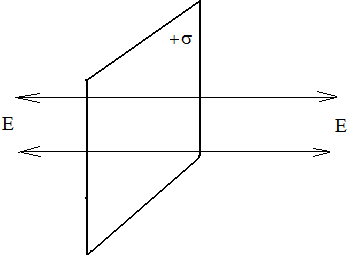
Поле создаваемое равномерно заряженной бесконечной плоскостью однородно и не зависит от расстояния до плоскости.
Напряженность поля между двумя бесконечными параллельными разноименно заряженными плоскостями.
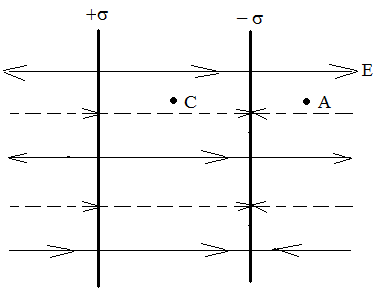
На рис. 9 дан вертикальный разрез плоскостей, поле положительно заряженной плоскости изображено сплошными силовыми линиями, поле отрицательно заряженной плоскости – прерывистыми. Так как по величине поверхностные плотности заряда плоскостей одинаковы то, согласно формуле (13)
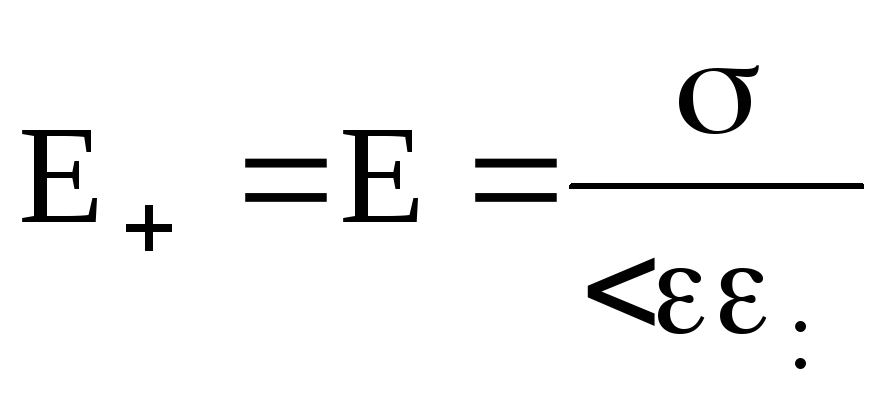 .
.
Как видно из рис.
9, поля между плоскостями складываются
(силовые линии направлены в одну сторону).
Поэтому напряженность поля между
плоскостями
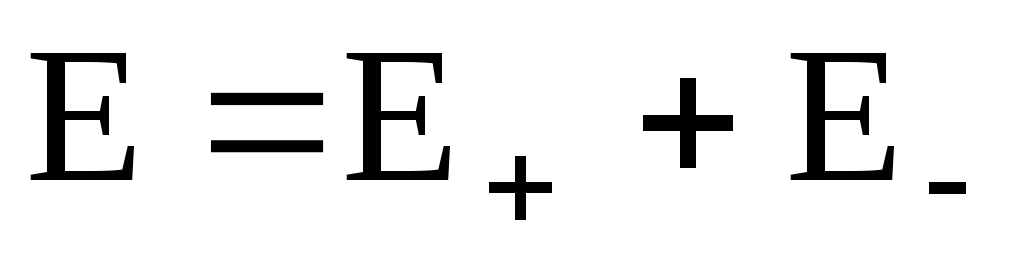 или
или
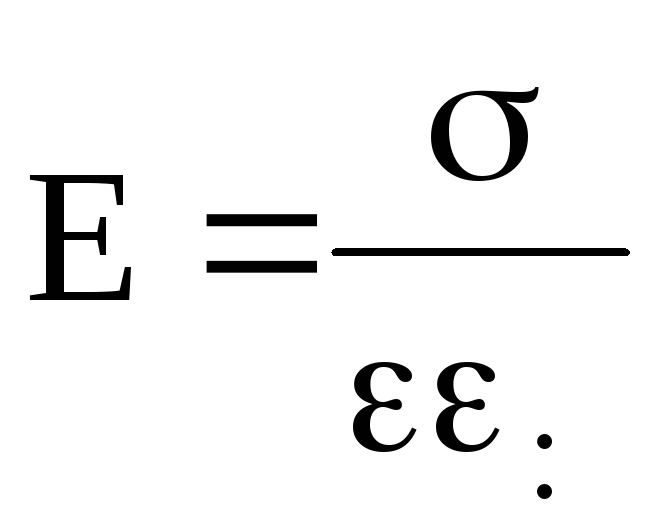 .
(14)
.
(14)
Слева и справа от плоскостей поля вычитаются (силовые линии направлены навстречу друг другу). Поэтому здесь напряженность поля Е=0.
При проектировании электронно-лучевых трубок, конденсаторов, электронных линз, фотоэлектронных умножителей и других приборов часто требуется знать направление вектора напряженности электростатического поля в любой точке пространства, заключенного между электродами сложной формы. Аналитический расчет поля удается только при самых простых конфигурациях электродов. Поэтому сложные электростатические поля исследуются экспериментально (как правило, методом моделирования электростатических полей в проводящих средах).
Сущность метода состоит в следующем. Изготовляют систему электродов, форма и взаимное расположение которых воспроизводят реальный прибор в некотором масштабе. На электроды подается напряжение. При этом между ними образуется электростатическое поле.
Если пространство между электродами заполнить проводящей средой, то возникнет электрический ток. Электростатическое поле сменится полем электрическим, которое легче поддается опытному исследованию.
При постоянном токе идет процесс электролитической поляризации, искажающей поле. Во избежание этого применяют переменный ток небольшой частоты (I=50 Гц).
Построение эквипотенциальных поверхностей в полях различной конфигурации в данной работе производится с помощью установки, схематически изображенной на рис. 7.
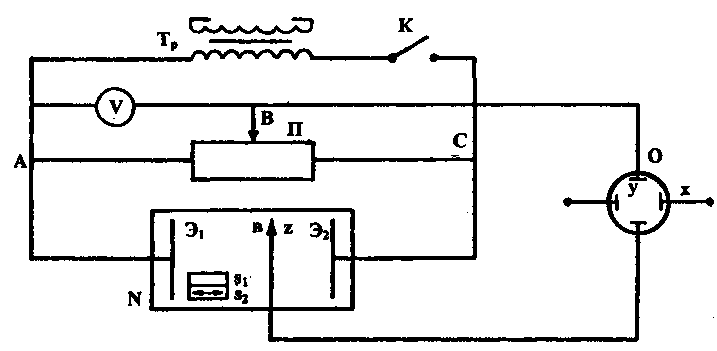
Она включает электролитическую ванну N, вольтметр, потенциометр П, ключ К и электроды Э 1 , Э 2 .
Порядок выполнения работы
В прямоугольную ванну N, заполненную электролитом (водой), помещают металлические электроды Э 1 и Э 2 , поле которых изучают. Электроды укреплены в держателях, опирающихся на стенки ванны. На зажимы электродов от трансформатора Т р подается переменное напряжение.
В измерительную часть схемы входят зонд Z (металлический стержень с острым концом), потенциометр, осциллограф, вольтметр.
Для исследования поля между электродами в него помещают зонд, соединенный через осциллограф с точкой В потенциометра. Потенциал точки В относительно электрода Э 1 измеряется вольтметром V. Если между зондом Z и точкой В имеется некоторая разность потенциалов, то на экране осциллографа появится синусоидальный сигнал, амплитуда которого пропорциональна разности потенциалов между ними.
Перемещая зонд Z, можно найти в ванне такую точку в, которая имеет такой же потенциал, как и точка В. В этом случае амплитуда сигнала на экране осциллографа будет минимальная (добиться ее нулевого значения не удается, т.к. при измерениях на переменном токе промышленной частоты неизбежны наводки на аппаратуру). Найдя ряд точек, потенциал которых соответствует потенциалу точки В, определяют эквипотенциальную линию.
С помощью держателей установить в ванне две плоские пластины, параллельные друг другу. На миллиметровой бумаге в некотором масштабе (на пример, 1:2 или 1:3) изобразить электроды и дно ванны, заключенное между ними.
Собрать электрическую цепь по схеме (рис. 7).
Включить осциллограф и прогреть его в течение 1-2 мин. При необходимости, используя ручку «фокус», добиться, чтобы светящаяся линия на экране стала тоньше.
Включить цепь.
Потенциометром установить разность потенциалов между точками А и В: U AB =0,1U. Держа зонд вертикально, перемещать его в области S 1 так, как показано (двойной стрелкой) на рис. 7, до тех пор, пока амплитуда сигнала, наблюдаемого на экране осциллографа, не будет минимальной. Найденную точку эквипотенциальной линии отметить на миллиметровой бумаге. Найти в ванне не менее 7-8 точек в разных ее областях, (а по ним всю линию равного потенциала) с φ 1 =0,1U.
Повторить измерения для φ 2 =0,3U, φ з =0,3U и т.д. Построить не менее 6 эквипотенциальных линий.
Установить потенциометром разность потенциалов между точками А и В, равную 0,5U. Мысленно выделить в ванне эквипотенциальную линию, потенциалы точек которой φ =0,5U. Поместить между пластинами кольцо из металла так, чтобы его диаметр совпал с выделенной эквипотенциальной линией. Выяснить, одинаковы или нет потенциалы точек, лежащих внутри кольца, на кольце. Начертить на миллиметровой бумаге эквипотенциальные линии при наличии между плоскими электродами кольца из проводящего материала, повторив операции (см. пп. 1,5,6).
Установить в ванне новые электроды и повторить операции (см. пп. 1,5,6).
Пользуясь данными измерений п. 5.6, построить график зависимости потенциала φ х точки между электродами от расстояния, отсчитываемого от электрода Э 1 .
10.Для поля, созданного плоскими электродами, найти напряженность поля по формуле (9) для четырех произвольно выбранных точек и построить линии напряженности.
11 .На всех трех графиках, построенных при выполнении пп. 6,7,8, вычертить линии напряженности.
Контрольные вопросы
Какое поле называется электростатическим?
Что такое напряженность электростатического поля, в каких единицах она измеряется?
Какое электростатическое поле называется однородным?
Дать определения потенциала, эквипотенциальной поверхности. Назвать единицы измерения потенциала.
Доказать, что силовые линии перпендикулярны эквипотенциальным поверхностям.
Вывести связь между напряженностью и потенциалом электростатического поля.
В чем заключается явление электростатической индукции, и где оно описывается в данной работе?
Каковы напряженность поля внутри кольца и потенциалы разных его точек?
Как записывается и читается теорема Остроградского-Гаусса? Каково ее назначение?
Лабораторная работа №2
Дальневосточный федеральный университет
Школа естественных наук
К лабораторной работе № 3.01
по дисциплине «физический практикум»
11200.62 – «физика»
Составители
Полищук Виталий Ефремович
Полищук Раиса федоровна
Владивосток
Издательский дом Дальневосточного федерального университета
ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Все известные в физике взаимодействия - гравитационное, электромагнитное, сильное и слабое - носят полевой характер. Физическое поле, наряду с веществом, является одним из видов материи. Электрическим полем называется вид материи, посредством которого взаимодействуют электрически заряженные тела. Заряженность тел характеризуют величиной заряда тела и обычно обозначают буквой q. Физическую величину, принятую за количественную меру заряженности тел, оцениваемую по способности к электрическому взаимодействию, называют зарядом.
В природесуществуют заряды двух видов, условно называемых положительными и отрицательными. Стабильной частицей, обладающей наименьшим отрицательным зарядом в свободном виде, является электрон ; соответственноположительным зарядом– протон. Заряды этих частиц по модулю равны с точностью до 10 -22 (с такой точностью проверена нейтральность атома), остальные же свойства у них различны (например, масса протона m p превышает массу электрона m e 1836 раз).
Электрические заряды характеризуются свойствами:
Дискретностью (квантованностью) - электрический заряд любой системы тел состоит из целого числа элементарных зарядов, кратных заряду электрона или протона.
Аддитивностью электрических зарядов – общий заряд Q системы, состоящей из N заряженных частиц, равен алгебраической сумме этих зарядов – Q= i .
Подчинению закону сохранения зарядов – алгебраическая сумма электрических зарядов тел или частиц, находящихся в изолированной системе, остается постоянной величиной, несмотря на любые взаимопревращения в этой системе.
Инвариантности - независимость заряда тела от скоростиегодвижения, т.е в любой системе отсчета величина заряда данного тела одинакова.
Взаимодействие электрических зарядов q 1 и q 2 есть результат действия электрического поля заряда q 1 на заряд q 2 и, соответственно, электрического поля заряда q 2 на заряд q 1 (при этом, одноименные заряды отталкиваются, а разноименные притягиваются). Заряд, всегда является источником электрического поля. Электрическое поле, создаваемое неподвижным зарядом или зарядами, называется электростатическим. Электростатическое поле – частный случай электромагнитного поля и в идеале существует только в инерциальных системах отсчета, где заряды неподвижны, так как любое движение электрических зарядов обуславливает возникновение и магнитного поля.
Основными характеристиками электростатического поля (как и любого другого) являются напряженность и потенциал .
Напряженность электрического поля E в данной точке - это физичес-кая величина, равная силе F , с которой электрическое поле действует на единичный пробный точечный заряд q, помещенный в эту точку
(). Пробный заряд - это заряд, собственное поле которого не ис-кажает поле, в которое он помещен. Напряженность - величина векто-рная и являетсясиловой характеристикой поля . Вектор напряжен-ности E имеет направление, совпадающее с направлением вектора си-лы, действующей на положительный заряд в данной точке поля. Согласно закону Кулона, сила F взаимодействия между двумя точечными зарядами определяется по формуле:
где q 1 -заряд создающий поле, q – заряд, на который действует поле, созданное зарядом q 1 , r – вектор, соединяющий источник поля (заряд q 1) и координату точки поля расположения заряда q.Тогда, из закона Кулона следует, что напряженность поля точечного заряда определяется по формуле:
Точечным зарядом называют заряженное тело, размерами которого можно пренебречь по сравнению с величиной r. В системе единиц СИ напряженность электрического поля измеряется в Н/Кл или В/м.
Электрические поля в линейных средах (среды, в которых нет сегнетоэлектриков) подчиняются принципу суперпозиции полей - их независимому сложению: если в данной точке пространства различные заряженные тела создают независимо электрические поля с напряженностями соответственно E 1 , E 2 , .. En , то вектор напряженности результирующего электрического поля E равен геометрической сумме векторов напряженностей всех электрических полей, т.е E=E 1 +E 2 +...+En. Чтобы описать электрическое поле в выделенном пространстве, нужно задать вектор напряженности в каждой точке поля. Эту зависимость можно представить не только аналитически, но и графически в виде семейства так называемых линий напряженности (силовых линий). Линией напряженности электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля в этой точке.Электростатическое поле - источниковое поле : его силовые линии (линии напряженности) не могут пересекаться, они начинаются на положительных и оканчиваются на отрицательных зарядах, или уходят в бесконечность от положительных зарядов и приходят из бесконечности к отрицательным зарядам.
Силовые линии проводятся с такой частотой, чтобы число линий, пронизывающих воображаемую площадку площадью, равной единице и перпендикулярную к силовым линиям было равно значению напряженности поля данной площадке. и поля в данном месте. Следовательно, по густоте силовых линий электрического поля можно судить не только о направлении, но и о значении напряженности поля.Электрическое поле, в котором напряженность одинакова по модулю и направлению в любой точке пространства называется однородным.
Электростатическое поле является потенциальным - это поле, работа сил которого не зависит от траектории движения заряда, а определяется начальной и конечной точками его перемещения, или, работа сил его по любой замкнутой траектории равна нулю.
Как известно, потенциальные поля количественно характеризуются потенциальной энергией. Энергетической характеристикой электростатического поля является потенциал . Потенциалом данной точки поля называют работу по перемещению единичного положительного заряда (q=1) силами поля из бесконечности в данную точку поля. Так как работа носит всегда относительный характер (определяется из какой точки в какую движется тело), то и потенциал любой точки поля зависит от выбора точки отсчета потенциала. Выбор точки отсчета потенциала называют нормировкой потенциала. Нормировка потенциала может быть любой, но чаще всего в физике используют его нормировку относительно бесконечно удаленных точек от источника поля (заряда q 1), принимая потенциал в этих точках за нуль потенциала. В электротехнике за нуль потенциала принимают потенциал Земли или проводника, связанного с ней. Разность потенциалов двух точек поля называют напряжением. Однако, разность потенциалов и напряжение численно равны друг другу только для потенциальных полей, к которым относится и электростатическое поле.
Напряжение и потенциал измеряются в системе СИ в вольтах (В). Потенциалом в 1В обладает точка поля, в которую для переноса заряда в 1Кл силами поля совершается работа в 1 Дж.
Принцип независимого сложения полей (принцип суперпозиции) позволяет рассчитать потенциал поля, создаваемого системой зарядов q 1 , q 2 ,…q n . Потенциал результирующего электростатического поля в данной точке, относительно выбранной нормировки, равен алгебраической сумме потенциалов полей, созданных каждым зарядом в отдельности: j = j 1 +j 2 ×××+j n . Потенциал - скалярная величина .
Значение потенциала в каждой точке пространства определяется величиной и конфигурацией заряда, создающего поле, а также расстоянием от источника поля до данной точки. Например, потенциал поля, создаваемого точечным зарядом q в вакууме, относительно бесконечности, определяется выражением:
где ε ο – электрическая постоянная вакуума, r-расстояние от источника поля заряда q до точки, в которой определяется потенциал поля. Если же поле создается протяженным зарядом, то потенциал j в этой точке определится более сложной формулой:
где ρ – объемная плотность заряда, V –объем заряженного тела.
Воображаемая поверхность, все точки на которой имеют одинаковый потенциал, называютсяповерхностями равного потенциала или эквипотенциальными поверхностями . Пользуясь понятием эквипотенциальной поверхности, можно изображать электрические поля графически, подобно тому, как это делается с помощью силовых линий. Пересекаясь с плоскостью чертежа, эквипотенциальные поверхности даютэквипотенциальные линии .
Работа поля по перемещению электрического заряда между двумя точками поля определяется формулой: A= q(j 1- j 2). Из формулы видно, что работа поля по перемещению заряда по эквипотенциальной поверхности равна нулю, т.к. все точки эквипотенциальной поверхности или линии характеризуются одинаковым потенциалом, а. это значит, что сила, действующая на заряд, все время перпендикулярна перемещению. Отсюда заключаем, что:
1. Линии напряженности (силовые линии) всегда перпендикулярны (ортогональны) к эквипотенциальным поверхностям (линиям). 2.Эквипотенциальные поверхности (линии) не пересекаются между собой.
Эквипотенциальные поверхности можно провести через любую точку поля, т.е. таких поверхностей можно провести бесконечное множество. Поэтому принято проводить эквипотенциальные поверх-ности (линии) таким образом, чтобы разность потенциалов для любых двух соседних поверхностей была одинаковой (j i +1 - j i) =const. В этом случае по густоте эквипотенциальных поверхностей (линий) можно качественно судить о величине напряженности поля – чем гуще располагаются эквипотенциальные поверхности тем больше напряженность.
Напряженность и потенциал электростатического поля связаны между собой формулой Е = - gradj. Из формулы следует, что в каждой точке поля вектор напряженности Е и вектор градиента потенциала j равны по величине и противопо- ложны по направлению.
На рисунке 1 сплошными линиями показаны эквипотенциальные линии (сплошные кривые) и линии напряженности (пунктирные кривые) для двух равных разноименных зарядов - диполя.
Из свойств ортогональности силовых линий и эквипотенциальных поверхностей вытекает возможность нахождения поверхности равного потенциала по силовым линиям поля. И, наоборот, по положению эквипотенциальных поверхностей – построение силовых линий поля. Последняя возможность используется в данной работе . Используя связь между напряженностью и разностью потенциалов Е =- gradφ, можно найти величину вектора напряженности на определенном участке поля. Если Δφ- разность потенциалов двух соседних эквипотенциальных линий, а Δx расстояние между ними, измеренное по силовой линии, то пользуясь приближенным соотношением по формуле Е= можно в однородном поле (или в неоднородном, но на очень малом расстоянии) найти модуль вектора напряженности на участке поля Δx.
 В данной работе проводится качественное изучение электростатического поля, графически отображаемое системой эквипотенциальных линий и ортогональной к ним системой линий напряженности поля. Теоретически, как правило, легче производить расчет потенциалов, чем напряженностей поля, так как первые являются скалярными величинами, а вторые – векторными. И экспериментально измерения потенциалов значительно проще, чем измерения напряженностей поля, так как основная часть приборов, применяемых для изучения полей, измеряют разности потенциалов, а не напряженности поля. Поэтому и в данной лабораторной работе экспериментально определяется значения потенциалов в разных точках поля, а не напряженностей. Силовые линии изучаемых полей строятся теоретически как система ортогональных кривых к экспериментально найденным эквипотенциальным поверхностям или эквипотенциальным линиям.
В данной работе проводится качественное изучение электростатического поля, графически отображаемое системой эквипотенциальных линий и ортогональной к ним системой линий напряженности поля. Теоретически, как правило, легче производить расчет потенциалов, чем напряженностей поля, так как первые являются скалярными величинами, а вторые – векторными. И экспериментально измерения потенциалов значительно проще, чем измерения напряженностей поля, так как основная часть приборов, применяемых для изучения полей, измеряют разности потенциалов, а не напряженности поля. Поэтому и в данной лабораторной работе экспериментально определяется значения потенциалов в разных точках поля, а не напряженностей. Силовые линии изучаемых полей строятся теоретически как система ортогональных кривых к экспериментально найденным эквипотенциальным поверхностям или эквипотенциальным линиям.
Для изучения распределения потенциалов в работе используется метод зондов. Его сущность заключается в том, что в исследуемую точку электрического поля вводится электрод - зонд . Зонд соединяется с прибором V, измеряющим величину потенциала зонда в данной точке поля относительно потенциала какой-нибудь другой выбранной точки поля, принятой за «нулевое» значение потенциала. При этом необходимо создать такие условия, чтобы зонд принял потенциал той точки поля, в которую он помещен. Только в этом случае показания измерительного прибора, соединенного с зондом, будут отражать правильную картину распределения потенциалов в исследуемом поле. Выполнить это условие в непроводящей среде трудно, что и привело к разработке особого метода изучения электростатических полей путем искусственного воспроизведения их структуры в проводящих средах, по которым пропускается постоянный ток. Следовательно, так как изучение электростатического поля при помощи зондов трудно осуществимо, то экспериментальное исследование электростатического поля заменяют изучением постоянного во времени электрического тока в слабо проводящих средах. Метод изучения электростатического поля путем создания другого эквивалентного ему поля называется моделированием.
В данной работе проводящей средой является слабый раствор поваренной соли, в которой смачивается лист писчей бумаги. Металлические электроды (Э1 и Э2) различной конфигурации устанавливаются на листе бумаги и на них подается постоянное напряжение от источника тока U. В измерительную часть установки входят зонд и цифровой вольтметр V (мультиметр) (рис.2).
Цель данной работы:
1. Экспериментальное исследование электростатического поля в области между заряженными проводниками различной конфигурации и описание его при помощи эквипотенциальных и силовых линий.
ВЫПОЛНЕНИЕ РАБОТЫ:
1.Пропитать в растворе поваренной соли лист бумаги и положить его на плоское стекло.
2.Установить плоские электроды на мокрой бумаге. Положение и форму электродов Э на бумаге отметить «пастовым» карандашом.
3.Включить питание установки. Вольтметром V с помощью зонда Zизмерить потенциал каждого электрода. Определить полярность электродов. Согласно схеме (рис.2) зонд Z на электроде Э2 покажет нулевое значение потенциала, принятое за нормировку (точку отсчета потенциала), а на электроде Э1 – максимальное, равное напряжению источника тока U. Следовательно, электрод Э2 имеет отрицательную полярность, а электрод Э1- положительную.
4.Перемещая зонд вблизи электрода с нулевым потенциалом, с помощью вольтметра найти на бумаге не менее 10 -15 точек с потенциалом 1,50В относительно нулевого. Точки на бумаге отметить пастовым карандашом и подписать значение потенциала. Плавная кривая, проведенная через найденные точки, даст эквипотенциальную линию с потенциалом 1,5В.
5.Выбрав «шаг» изменения потенциала ΔU=0,5 В повторить измерения пункта 4 для потенциалов 2; 2,5; 3; 3,5;4В …вплоть до величины потенциала на электроде Э 1 .
6.По указанию преподавателя, пункты 1-5 повторить для других предложенных систем электродов, моделирующих поле точечного заряда, поле диполя, поле сложной системы точечного заряда и плоскости.
7.После просушки листов бумаги, соединить имеющиеся на них точки равного потенциала эквипотенциальными линиями. Построить картину силовых линий (указав их направление) для исследованных пар электродов. Кривые надо стараться проводить не прямо через точки, а так, чтобы они не имели резких перегибов и изломов.
8.В 4-5 точках поля «плоского конденсатора» рассчитать по формуле Е= модуль вектора напряженности на участке поля Δx. В формуле Δφ- разность потенциалов двух соседних эквипотенциальных линий, а Δx расстояние между ними, измеренное по силовой линии.
ТЕОРИЯ ПОЛЯ
Теория поля есть учение об электрических и магнитных явлениях, о теоретических положениях и законах, которым подчиняются эти явления и о вытекающих из них методах расчета.
Электромагнитное поле является особым видом материи, оно является носителем энергии и обладает специфическими (присущими только ему) электрическими и магнитными свойствами. Изложение основных свойств и методов расчета полей произведем в порядке перехода от более простых к более сложным. В соответствии с этим в начале рассмотрим поля, неизменные во времени, и только после этого изучим переменное электромагнитное поле. Изучение всех видов полей расширяет физические представления о поле, известные и курса физики, способствует более глубокому пониманию процессов, происходящих в электротехнических устройствах, важно с прикладной точки зрения, т.к. дает возможность решать многие задачи, имеющие существенное значение не только для теории электрических цепей, но и более общих задач (излучение и канализация электрической энергии и др.).
Мы будем изучать только поля в однородных (одинаковых во всех точках поля) и изотропных (со свойствами, не зависящими от интенсивности поля) средах.
Электростатическое поле
Электростатическое поле является частным случаем электромагнитного, оно создается неподвижными в пространстве (относительно наблюдателя) и неизменными во времени зарядами. Непосредственно на органы чувств человека электростатическое поле не воздействует, но ему присуща способность воздействовать с механической силой на помещенный в него пробный заряд. Это воздействие и положено в основу обнаружения электростатического поля и определения его интенсивности.
Основными величинами,
характеризующими свойства этого поля
являются его напряженность и потенциал.
Если в электростатическое поле поместить
настолько малый пробный заряд, что он
своим присутствием не исказит его, то
на него будет действовать сила
Отношение этой силы к
величине заряда и даст напряженность
поля
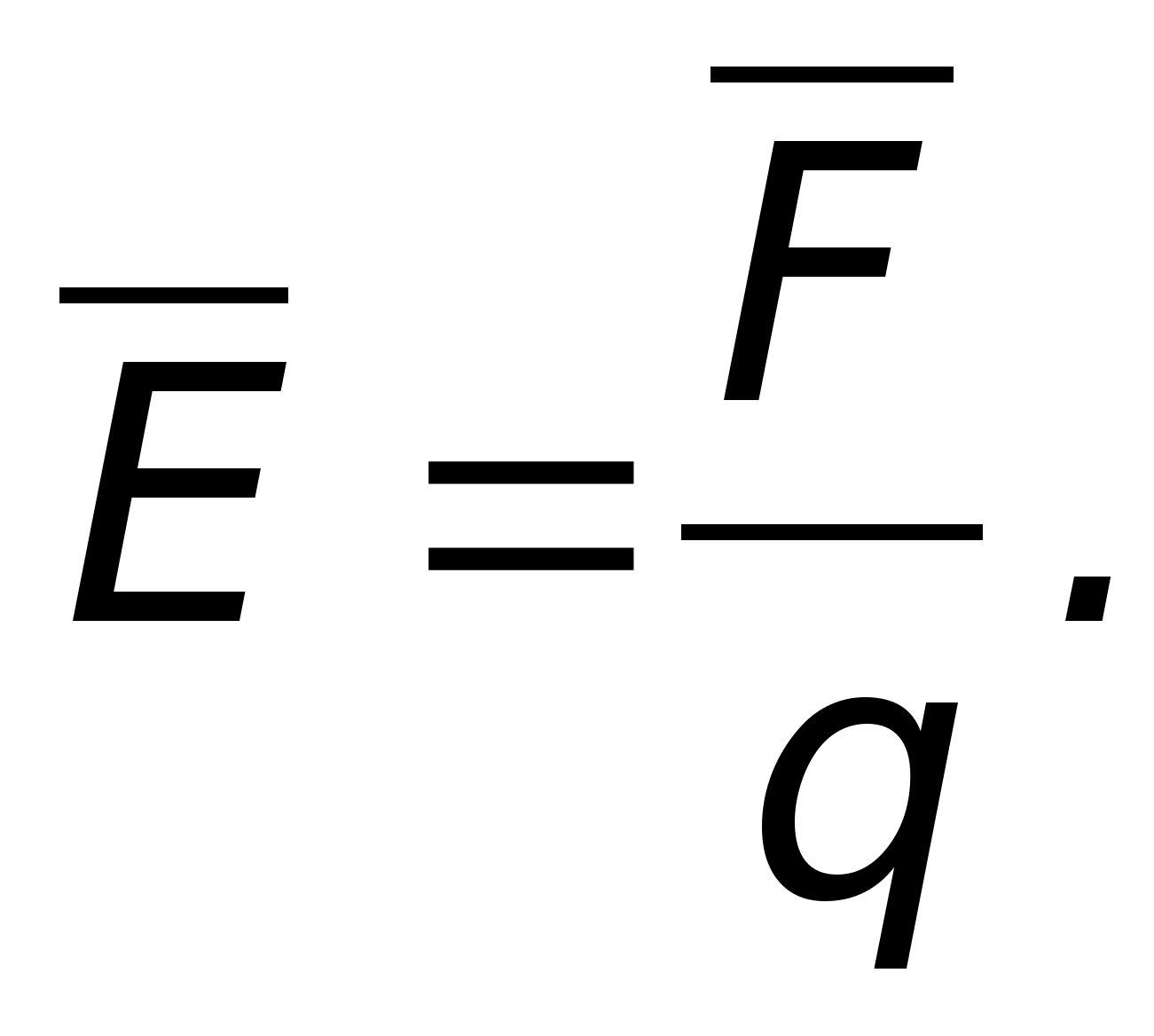 Если
Если
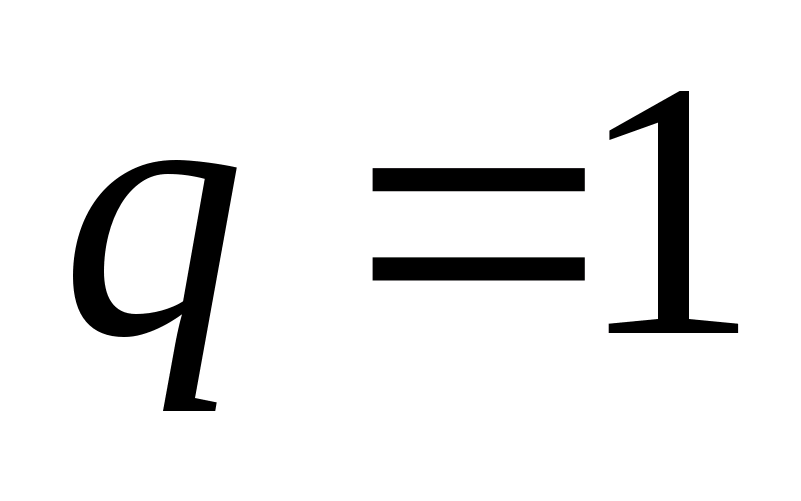 ,
то
,
то
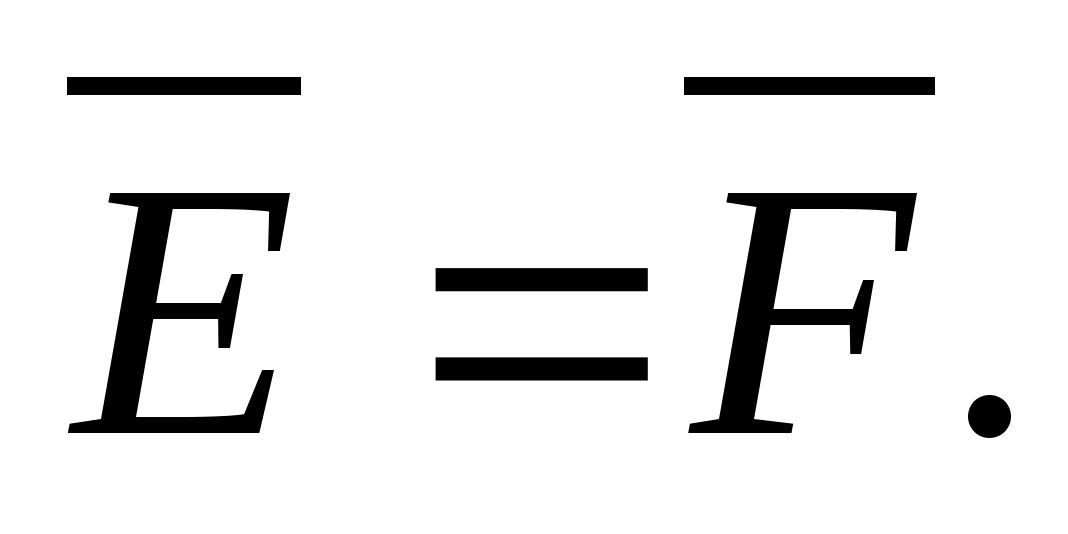 Отсюда следует, что напряженность поля
равна силе, действующей на единичный
положительный заряд, она характеризует
интенсивность поля. Единица измерения
напряженности
Отсюда следует, что напряженность поля
равна силе, действующей на единичный
положительный заряд, она характеризует
интенсивность поля. Единица измерения
напряженности
Д опустим,
что в некотором электростатическом
поле единичный положительный пробный
заряд под действием сил поля переместился
из точки 1 в точку 2 (рис.11.1). Тогда
опустим,
что в некотором электростатическом
поле единичный положительный пробный
заряд под действием сил поля переместился
из точки 1 в точку 2 (рис.11.1). Тогда
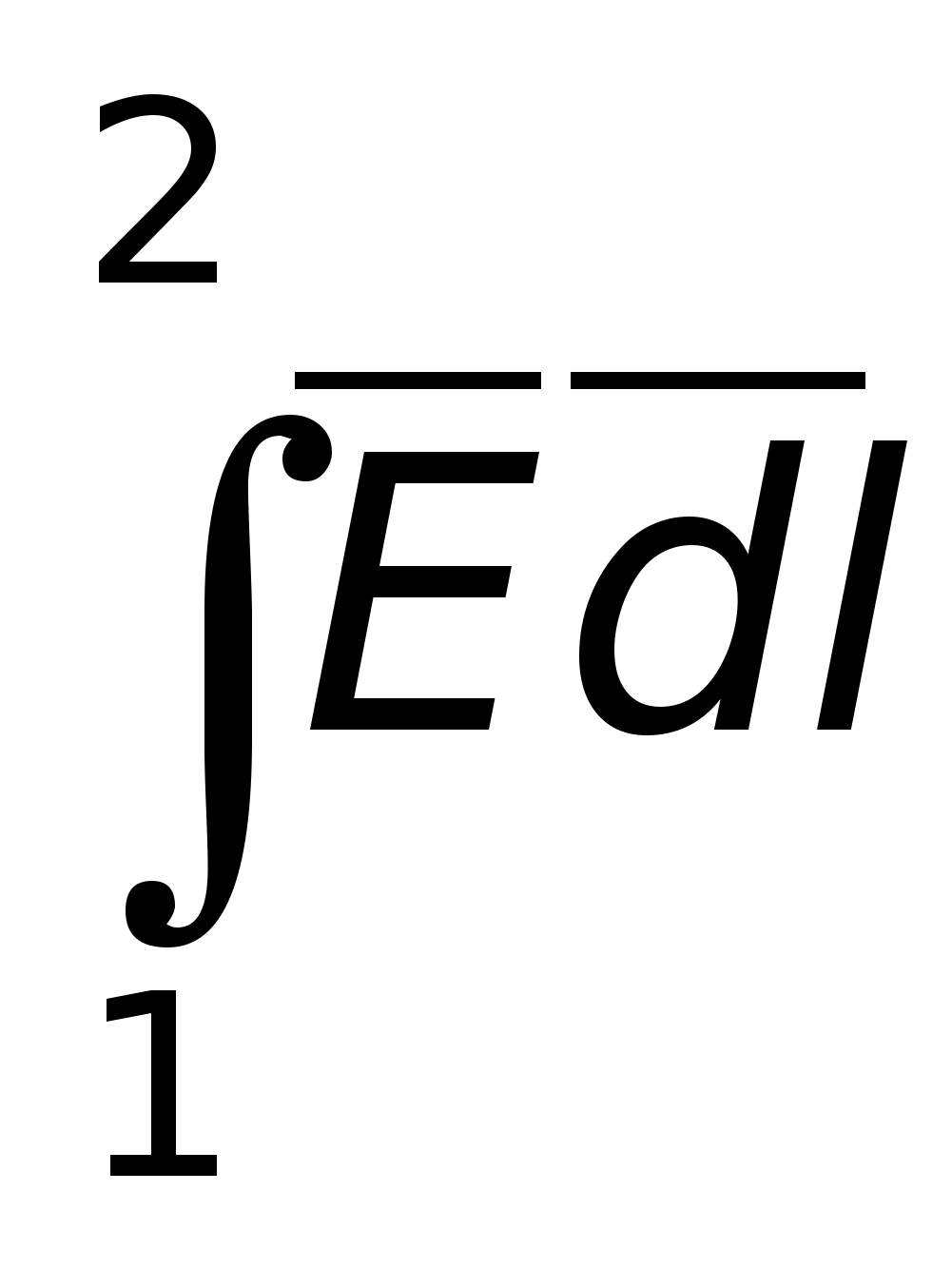 даст работу по перемещению этого заряда
из т.1 в т.2. Из курса физики известно, что
работа поп перемещению единичного
положительного заряда из одной точки
в другую есть напряжение или разность
потенциалов, т.е.
даст работу по перемещению этого заряда
из т.1 в т.2. Из курса физики известно, что
работа поп перемещению единичного
положительного заряда из одной точки
в другую есть напряжение или разность
потенциалов, т.е.
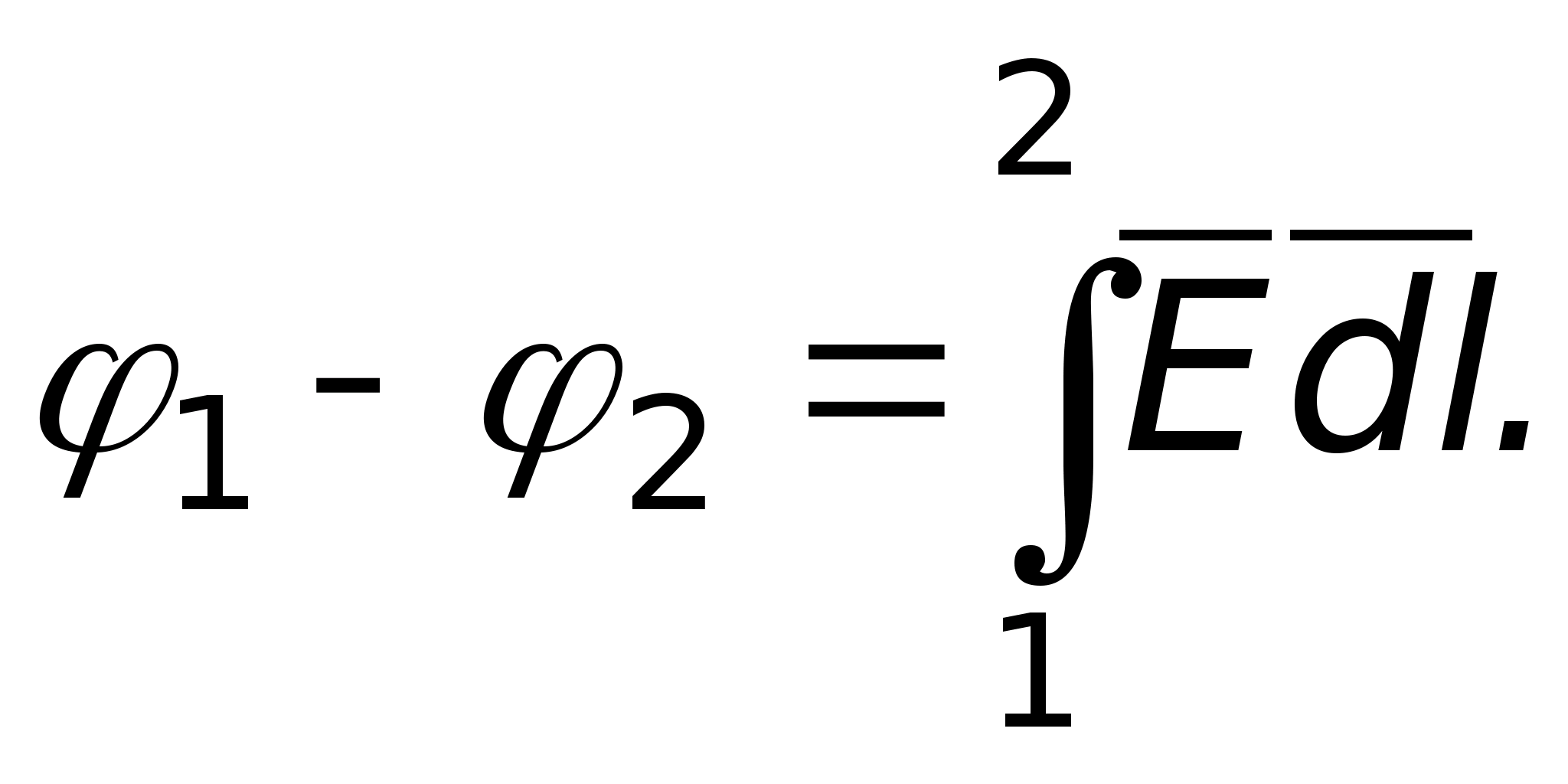 Если
Если
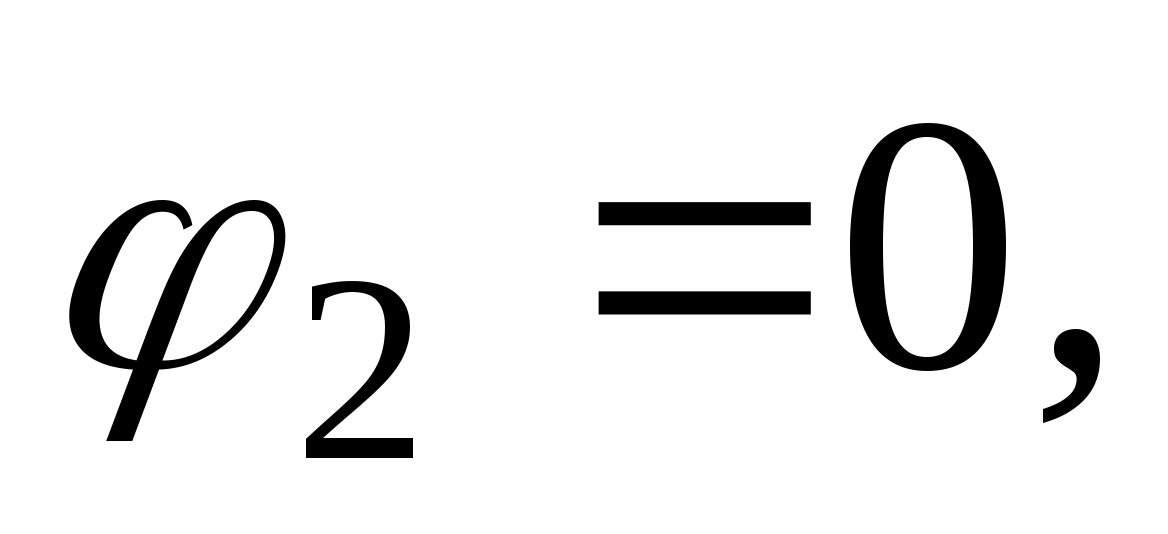 то
то
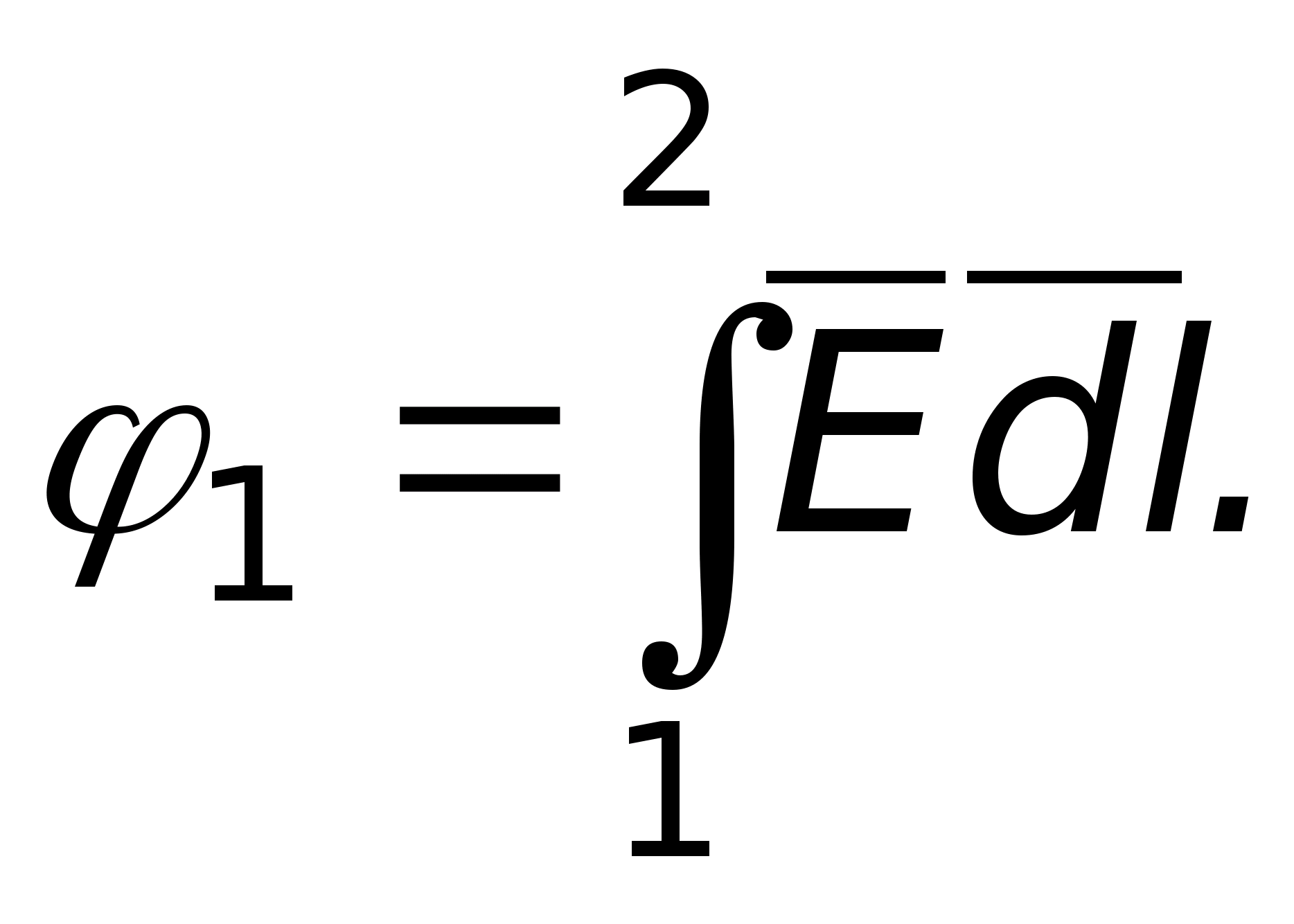 Отсюда следует, что потенциал некоторой
точки есть работа по перемещению
единичного положительного заряда из
данной точку в ту, потенциал которой
равен нулю. В качестве точки, имеющей
нулевой потенциал, может быть выбрана
любая. Часто её помещают в бесконечность,
иногда на поверхность земли. Если точка
с нулевым потенциалом выбрана, то
совершенно однозначно определяются
потенциалы всех остальных точек. Из
рассмотренного видно, что потенциал
определяется с точностью до постоянной,
зависящей от того куда помещается точка
с нулевым потенциалом. В связи с этим
связь между потенциалом и напряженностью
записывают так:
Отсюда следует, что потенциал некоторой
точки есть работа по перемещению
единичного положительного заряда из
данной точку в ту, потенциал которой
равен нулю. В качестве точки, имеющей
нулевой потенциал, может быть выбрана
любая. Часто её помещают в бесконечность,
иногда на поверхность земли. Если точка
с нулевым потенциалом выбрана, то
совершенно однозначно определяются
потенциалы всех остальных точек. Из
рассмотренного видно, что потенциал
определяется с точностью до постоянной,
зависящей от того куда помещается точка
с нулевым потенциалом. В связи с этим
связь между потенциалом и напряженностью
записывают так:
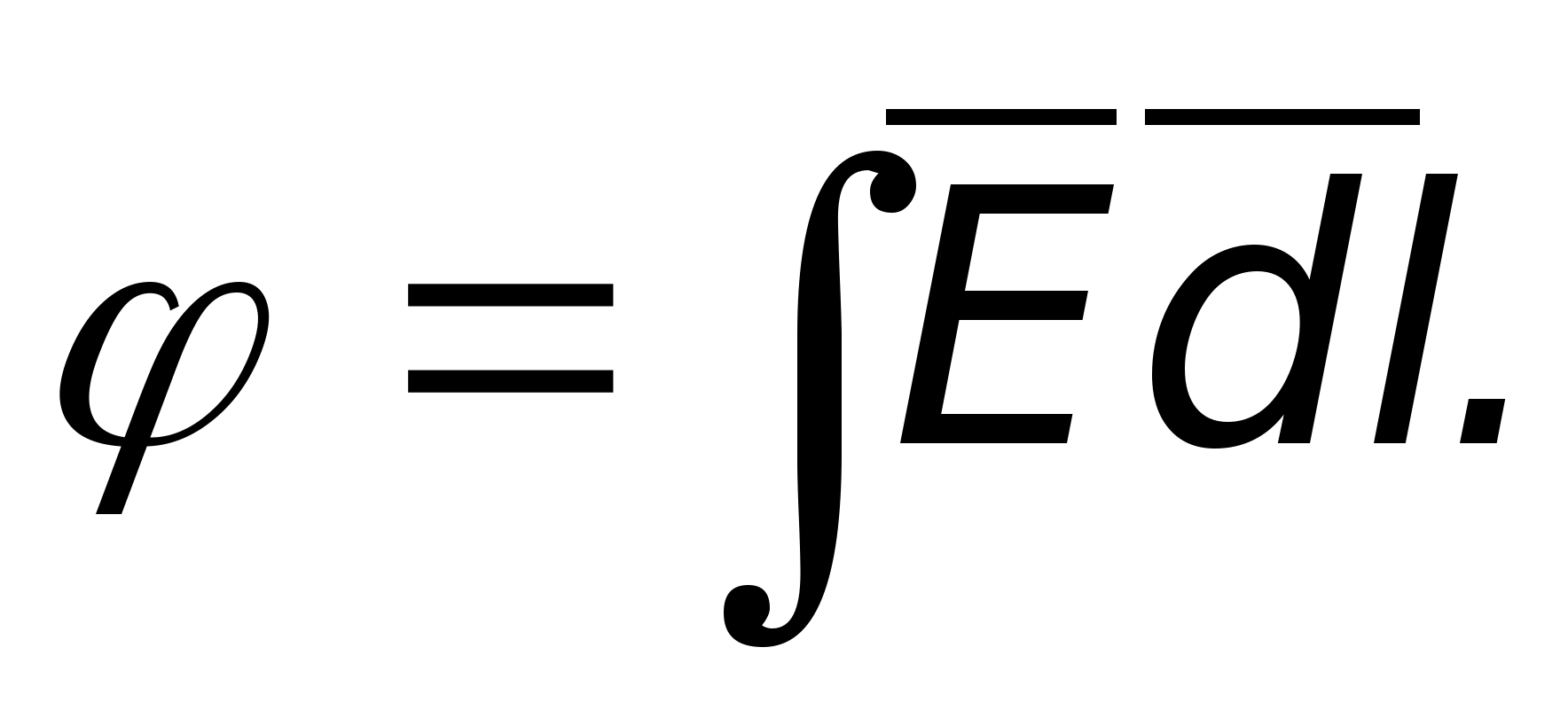 Тот факт, что потенциал определяется с
точностью до постоянной практического
значения не имеет, т.к. важно напряжение,
которое равно разности потенциалов, а
при её взятии постоянная интегрирования
уничтожается.
Тот факт, что потенциал определяется с
точностью до постоянной практического
значения не имеет, т.к. важно напряжение,
которое равно разности потенциалов, а
при её взятии постоянная интегрирования
уничтожается.
Если
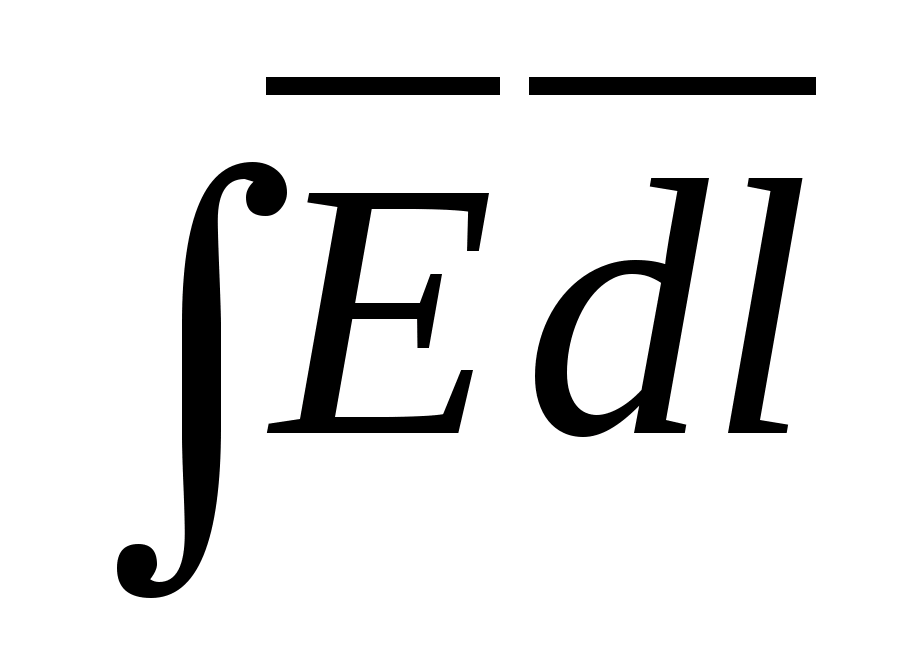 взять по замкнутому контуру, то он даст
ноль, т.е.
взять по замкнутому контуру, то он даст
ноль, т.е.
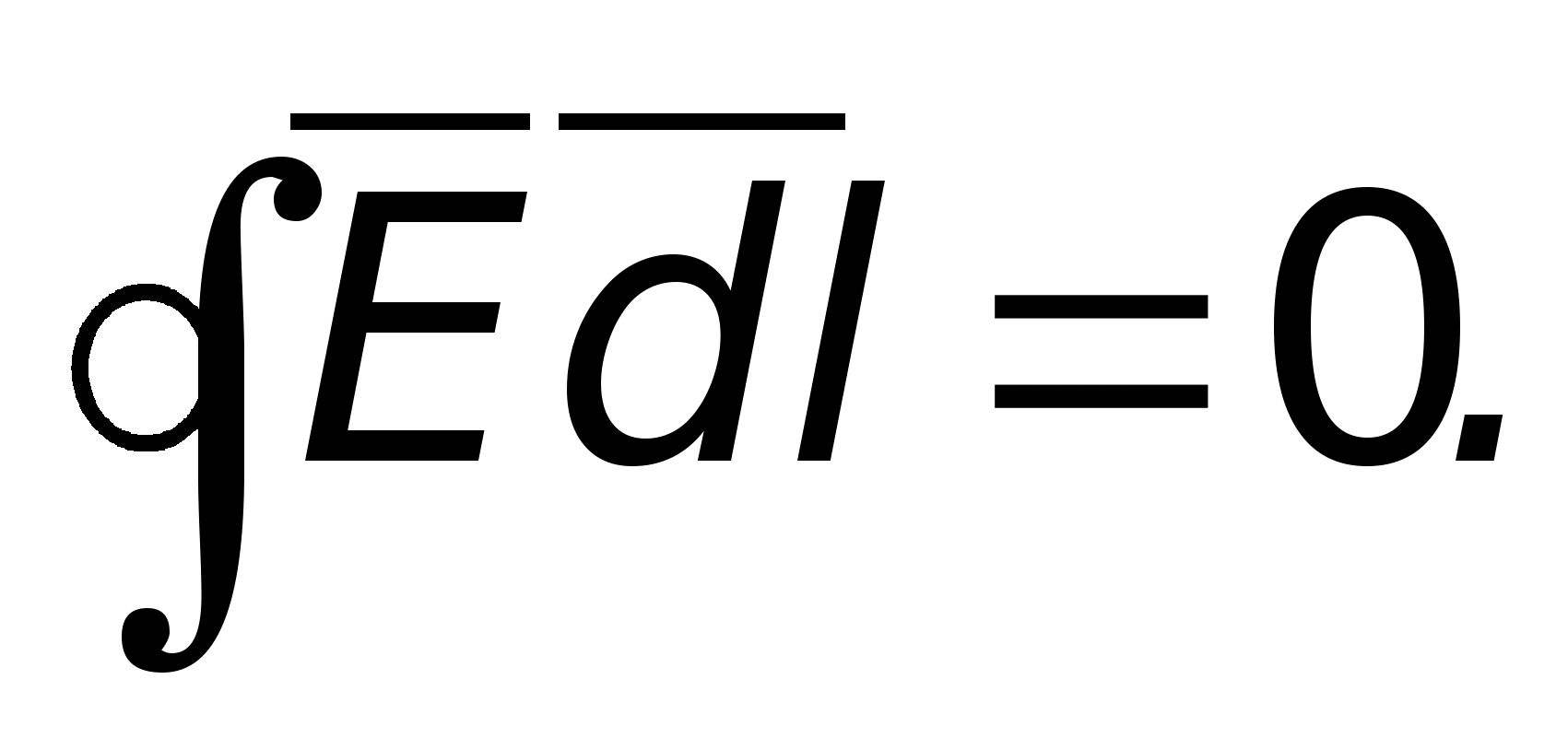 Это означает, что при движении вдоль
замкнутого контура совершается
определенная работа силами поля и точно
такая же работа выполняется против сил
поля. Соотношение
Это означает, что при движении вдоль
замкнутого контура совершается
определенная работа силами поля и точно
такая же работа выполняется против сил
поля. Соотношение
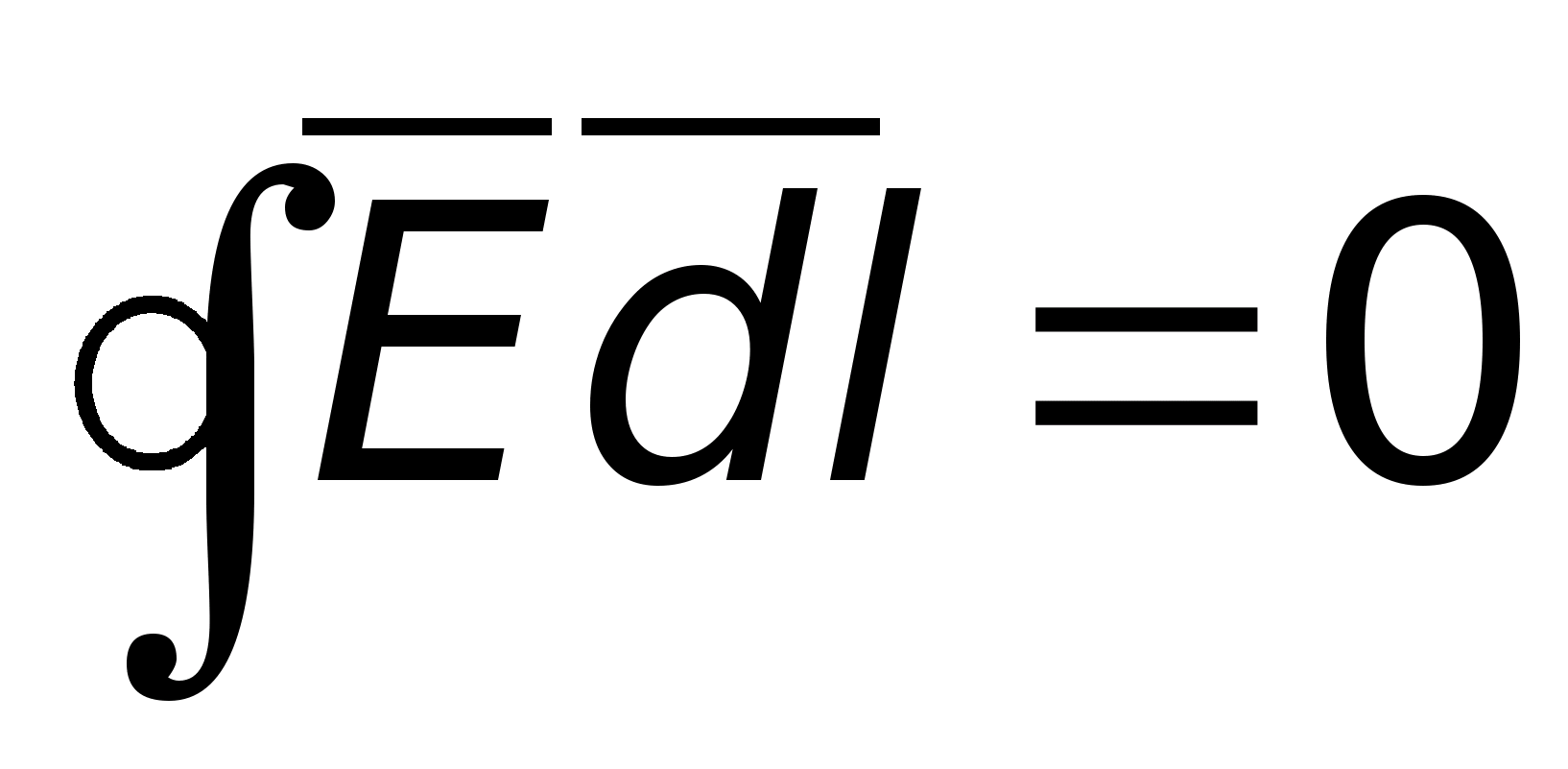 выражает одно из основных свойств
электростатического поля - оно является
потенциальным (потенциальными являются
все поля, для которых выполняется
подобное соотношение – гравитационные,
тепловые и т.д.).
выражает одно из основных свойств
электростатического поля - оно является
потенциальным (потенциальными являются
все поля, для которых выполняется
подобное соотношение – гравитационные,
тепловые и т.д.).
Графическая картина электростатического поля
Электростатическое поле определено, если известен закон изменения напряженности и потенциала в функции координат. Нагляднее же его можно охарактеризовать совокупностью силовых и эквипотенциальных линий, которая и называется его графической картиной. Силовой называется такая мысленно проведенная в поле линия, которая начинается на положительно заряженном теле, заканчивается на отрицательно заряженном теле и касательная к которой в любой точке дает направление вектора Е . Вдоль силовой линии перемещался бы весьма малый положительный заряд, имеющий возможность свободно двигаться и не обладающий инерцией. Так как положительный и отрицательный заряды не могут находиться в одной точке, то силовые линии имеют начало и конец, они не могут быть замкнутыми сами на себя. В любом электростатическом поле могут быть проведены эквипотенциальные поверхности как совокупности точек, имеющих один и тот же потенциал. Если поле рассечь какой либо плоскостью, то в полученном сечении будут видны следы эквипотенциальных поверхностей, которые и называются эквипотенциальными линиями. В противоположность силовым эквипотенциальные линии являются непрерывными, замкнутыми сами на себя. В любой точке поля силовые и эквипотенциальные линии перпендикулярны друг другу. Для примера приведем графическую картину электростатического поля двух точечных зарядов (рис.11.2).
C вязь между напряженностью поля и потенциалом
Выясненная ранее взаимосвязь
напряженности и потенциала
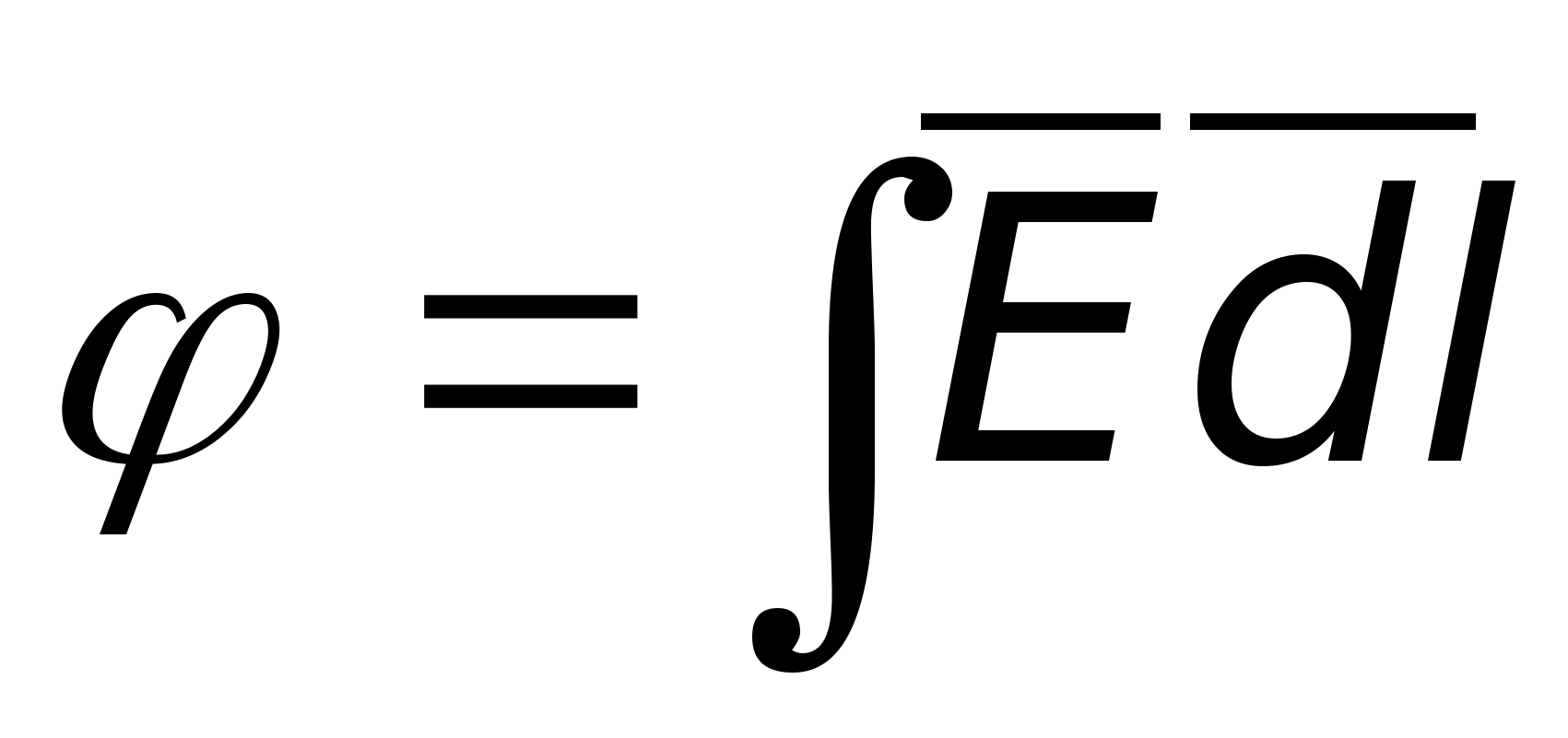 называется интегральной. На практике
же чаще используется дифференциальная
связь между этими величинами для
выяснения которой выделим в некотором
электростатическом поле две
эквипотенциальные линии (рис.11.3). Пусть
все точки первой линии обладают
потенциалом φ
1 ,
а второй – φ
2 .
Для определенности будем полагать, что
φ
1 >φ
2 ,
но отличаются они на бесконечно малую
величину, т.е. φ
1 -φ
2 =d
φ
.
Расстояние между линиями – dl
.
Выберем на первой линии
произвольную точку 1, а на второй – точку
2. Если разность потенциалов между этими
точками поделить на кратчайшее расстояние
между ними (по прямой), то п
называется интегральной. На практике
же чаще используется дифференциальная
связь между этими величинами для
выяснения которой выделим в некотором
электростатическом поле две
эквипотенциальные линии (рис.11.3). Пусть
все точки первой линии обладают
потенциалом φ
1 ,
а второй – φ
2 .
Для определенности будем полагать, что
φ
1 >φ
2 ,
но отличаются они на бесконечно малую
величину, т.е. φ
1 -φ
2 =d
φ
.
Расстояние между линиями – dl
.
Выберем на первой линии
произвольную точку 1, а на второй – точку
2. Если разность потенциалов между этими
точками поделить на кратчайшее расстояние
между ними (по прямой), то п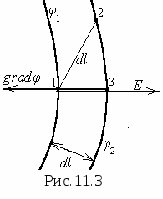 олученная
величина будет характеризовать скорость
изменения потенциала в направлении
кратчайшего расстояния между точками.
Эта скорость зависит от того, как выбраны
точки. Если, например, точку 2 смещать
вверх, то она упадет, поскольку не d
φ
изменится, а расстояние между точками
возрастет. Если т.2 смещать вниз, то
происходит возрастание указанной
скорости. Когда т.2 займет положение,
наиболее близкое к т.1 (т.3), скорость
изменения потенциала станет максимальной.
В математике вводится понятие градиента
скалярной функции, как скорости её
изменения, взятой в направлении
наибольшего возрастания. Применим это
понятие к потенциалу, т.е. рассмотрим
grad
φ
.
Это будет вектор – он
имеет направление от т.3 к т.1 (направление
наибольшего возрастания), а его модуль
равен
олученная
величина будет характеризовать скорость
изменения потенциала в направлении
кратчайшего расстояния между точками.
Эта скорость зависит от того, как выбраны
точки. Если, например, точку 2 смещать
вверх, то она упадет, поскольку не d
φ
изменится, а расстояние между точками
возрастет. Если т.2 смещать вниз, то
происходит возрастание указанной
скорости. Когда т.2 займет положение,
наиболее близкое к т.1 (т.3), скорость
изменения потенциала станет максимальной.
В математике вводится понятие градиента
скалярной функции, как скорости её
изменения, взятой в направлении
наибольшего возрастания. Применим это
понятие к потенциалу, т.е. рассмотрим
grad
φ
.
Это будет вектор – он
имеет направление от т.3 к т.1 (направление
наибольшего возрастания), а его модуль
равен
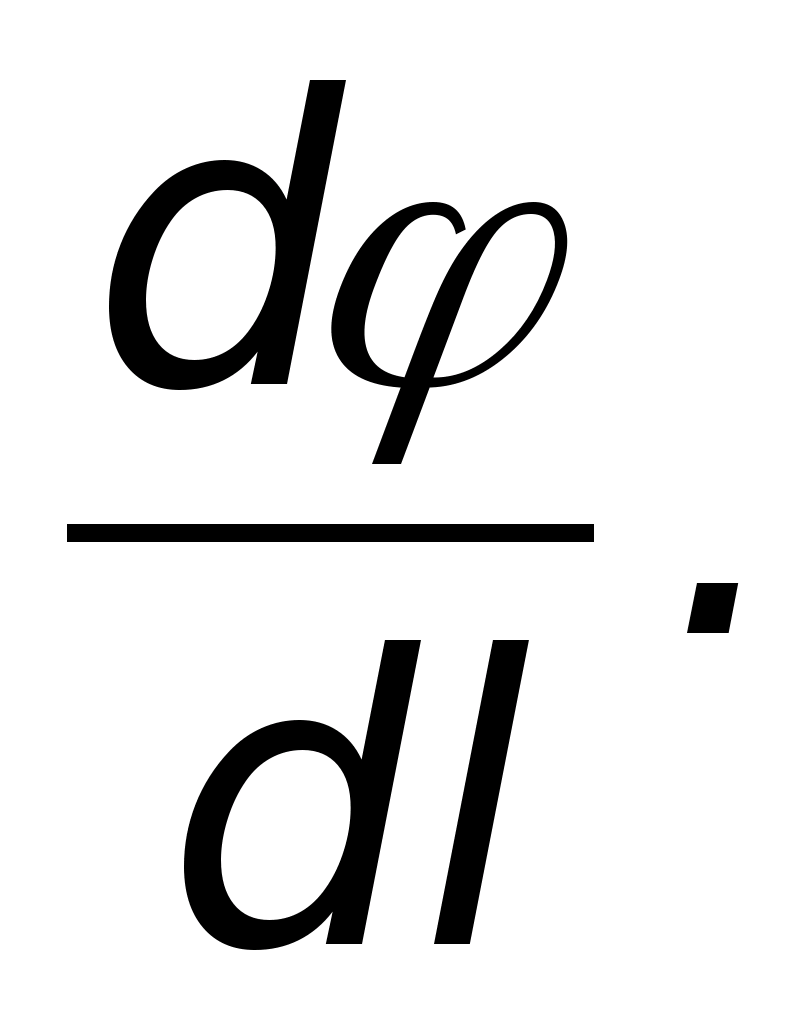 Напряженность поля направлена
от более высокого
потенциала (φ
1)
к меньшему (φ
2),
а её модуль равен
Напряженность поля направлена
от более высокого
потенциала (φ
1)
к меньшему (φ
2),
а её модуль равен
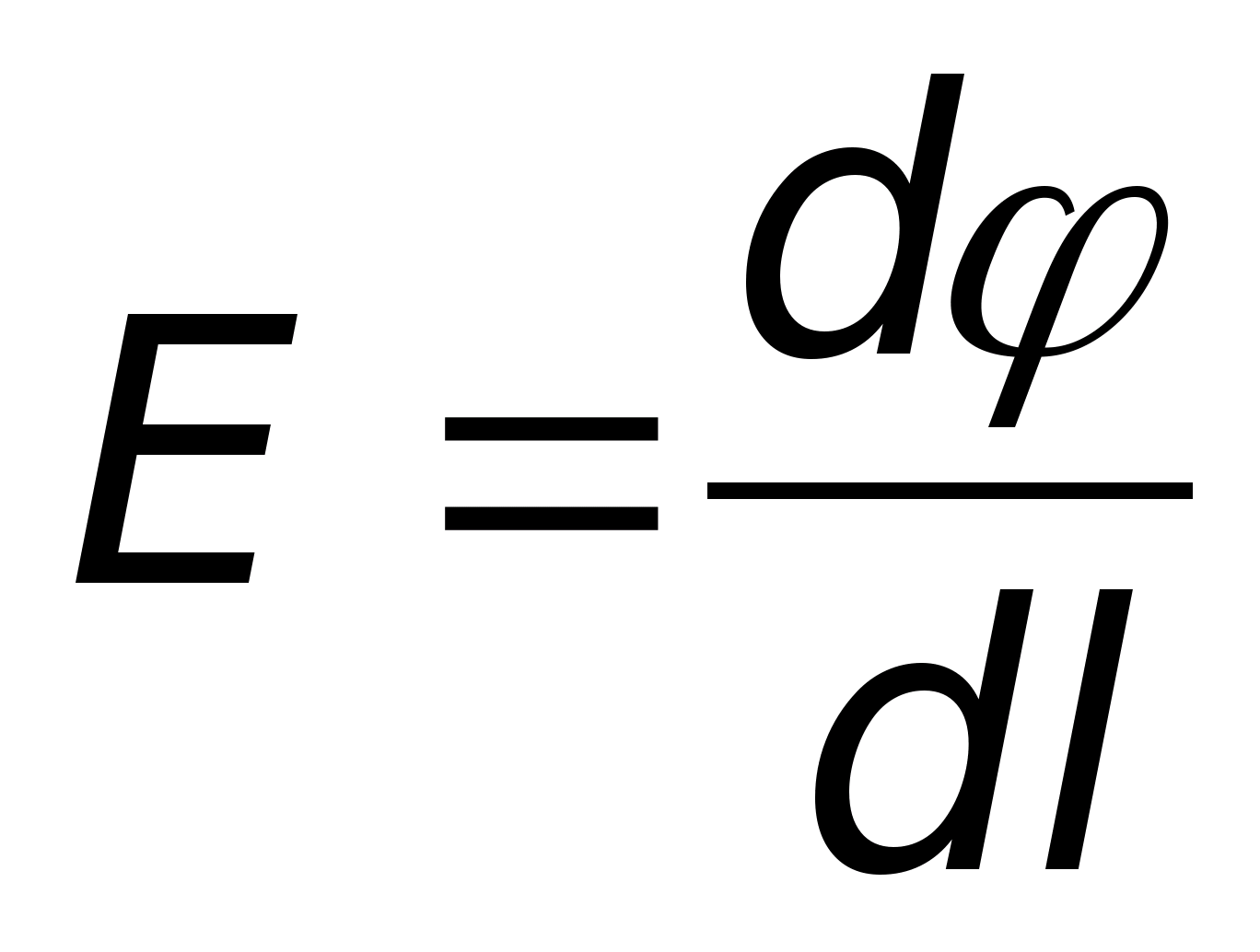 (см. интегральную форму). Поскольку
модули векторов Е
и gradφ
одинаковы,
а направлены они в противоположные
стороны, то
(см. интегральную форму). Поскольку
модули векторов Е
и gradφ
одинаковы,
а направлены они в противоположные
стороны, то
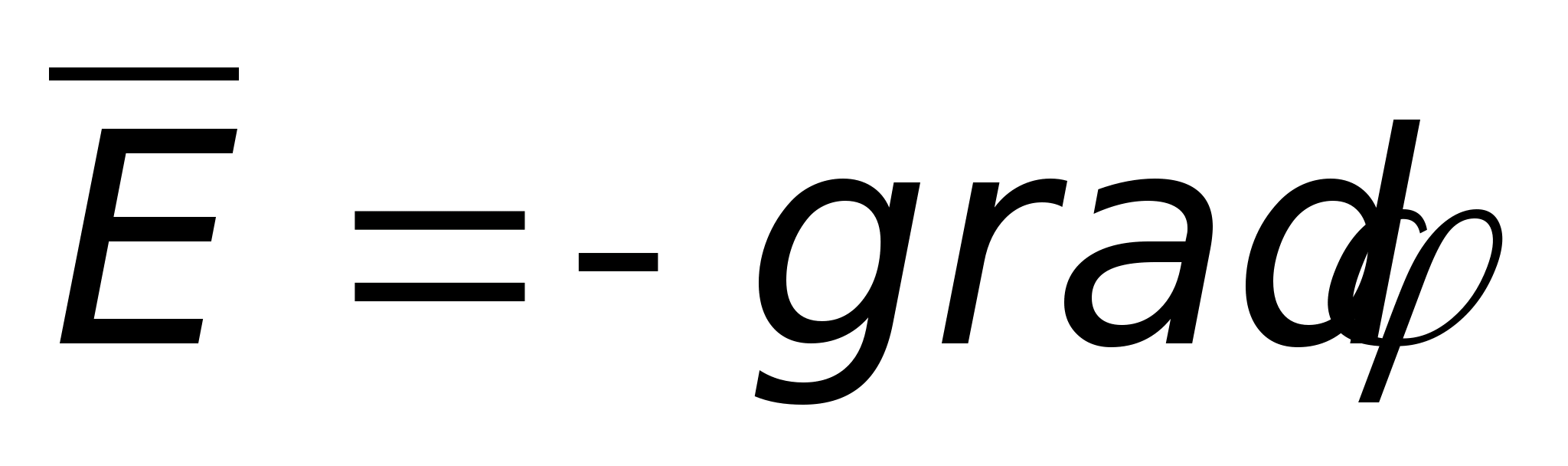 .
.
Направление
наибольшего возрастания потенциала в
общем случае не совпадает ни с какой
координатной осью, поэтому grad
φ
представляется в виде
суммы проекций по координатным осям,
например, в прямоугольной системе
координат (рис.11.4)
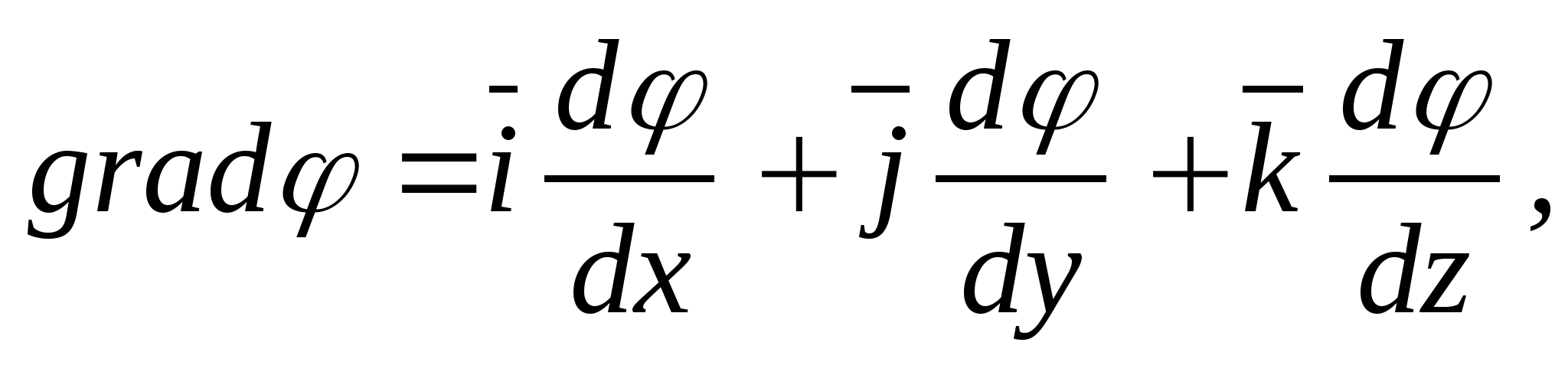 где
где
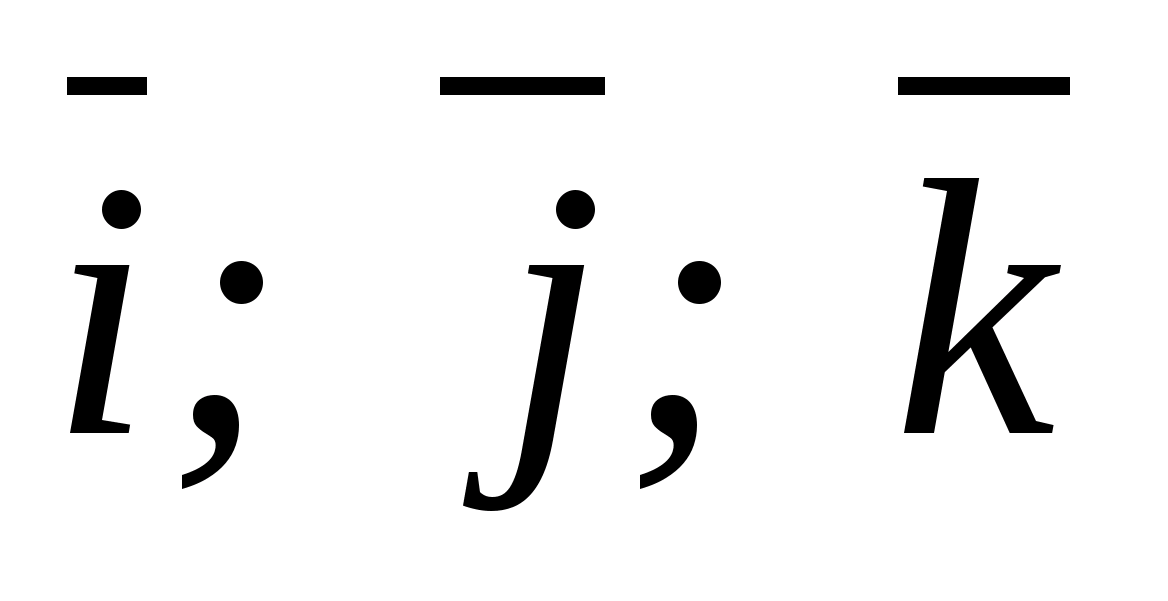 - орты (единичные векторы) прямоугольной
системы,
- орты (единичные векторы) прямоугольной
системы,
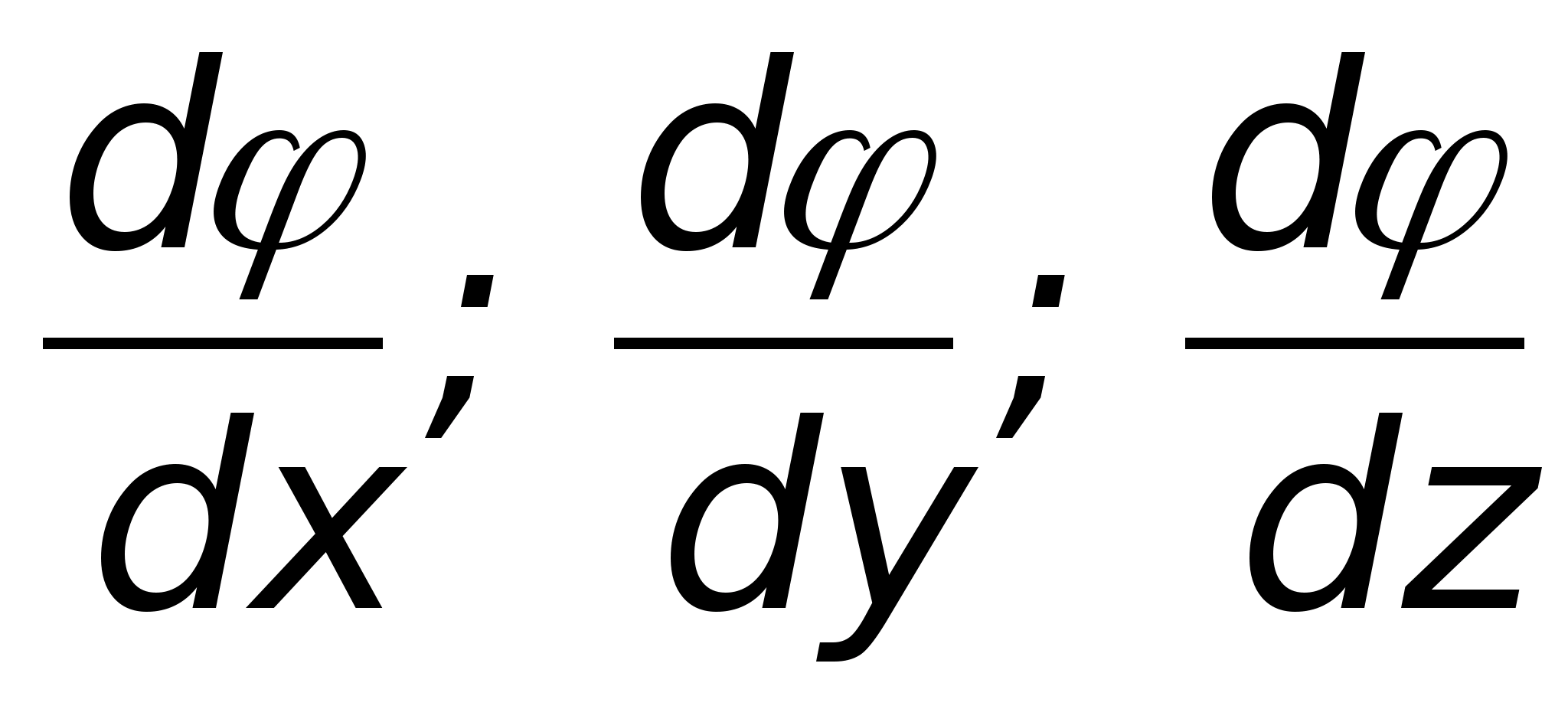 - скорости изменения потенциала вдоль
соответствующей оси. Напряженность Е
также может быть записана через проекции
- скорости изменения потенциала вдоль
соответствующей оси. Напряженность Е
также может быть записана через проекции
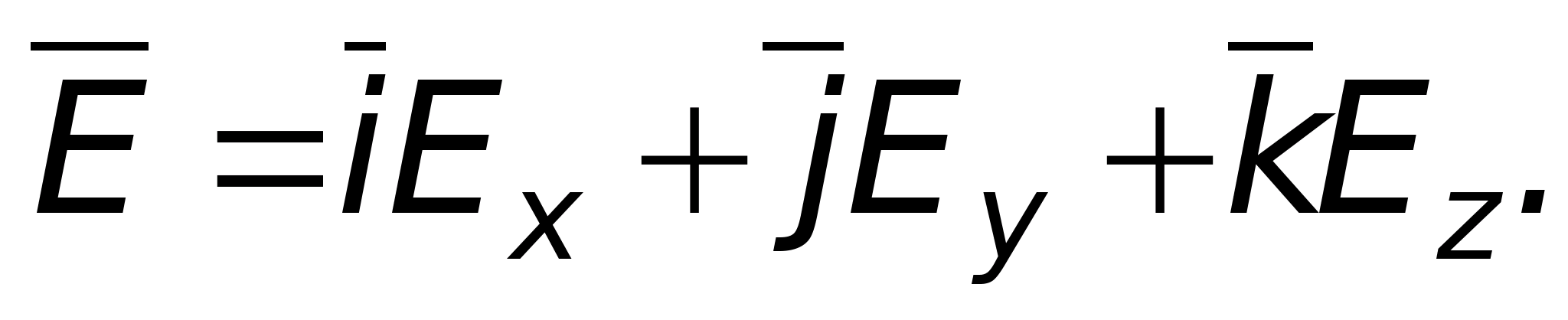 Два вектора равны друг другу, если у них
одинаковы проекции, т.е.
Два вектора равны друг другу, если у них
одинаковы проекции, т.е.
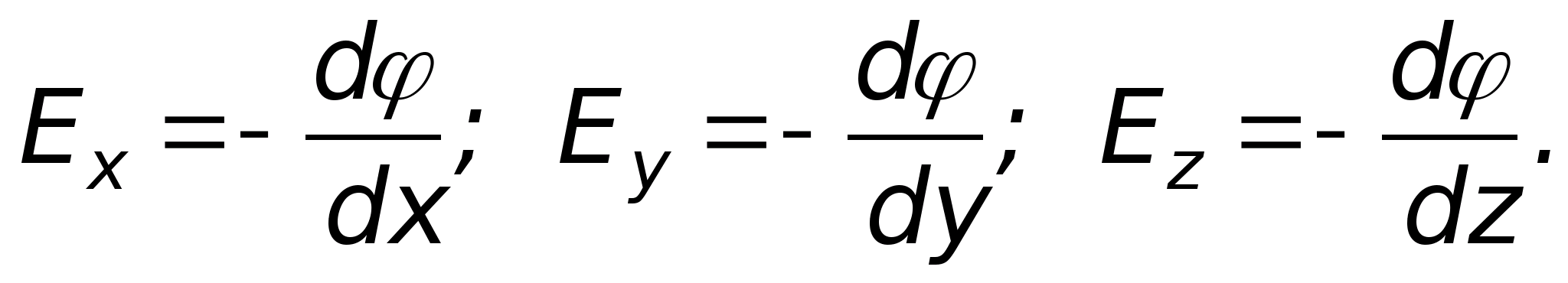 Именно последние три формулы используются
в практических расчетах.
Именно последние три формулы используются
в практических расчетах.
Для сокращения записи различных
операций в теории поля широко используется
не имеющий физического смысла
дифференциальный оператор Гамильтона
(набла), под которым понимают сумму
частных производных по координатным
осям, умноженных на соответствующие
орты. В декартовой системе координат
он имеет вид:
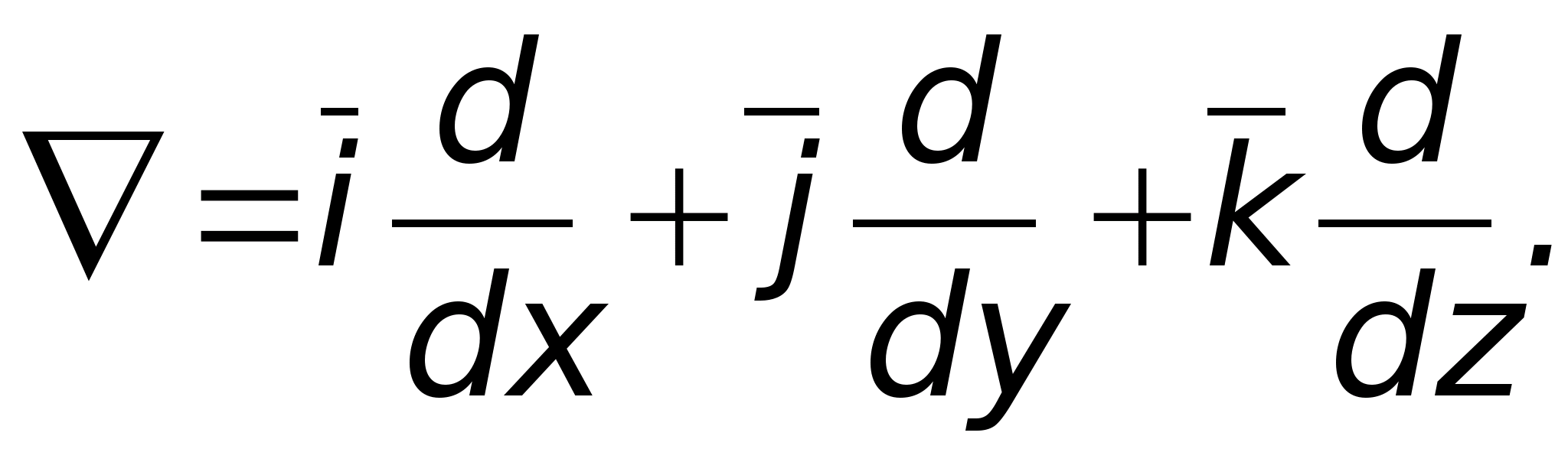 Формально набла можно рассматривать
как вектор. Он может быть применен как
к скалярной, так и к векторной функции.
Та функция, действие над которой
производят (дифференцирование по
координатным осям или пространственное
дифференцирование) пишется справа от
Формально набла можно рассматривать
как вектор. Он может быть применен как
к скалярной, так и к векторной функции.
Та функция, действие над которой
производят (дифференцирование по
координатным осям или пространственное
дифференцирование) пишется справа от
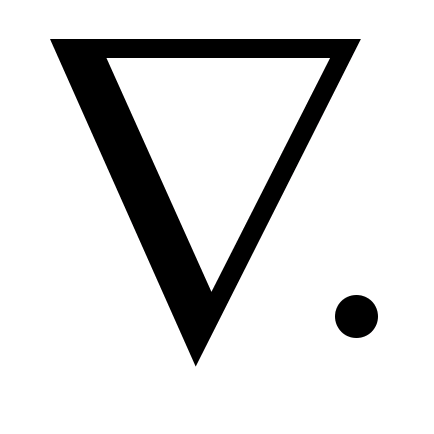 Если справа от
Если справа от не
указана функция, то сам по себе оператор
набла не применяется (аналогично как
sin, log
и т.д.). Применив оператор набла к
потенциалу
не
указана функция, то сам по себе оператор
набла не применяется (аналогично как
sin, log
и т.д.). Применив оператор набла к
потенциалу
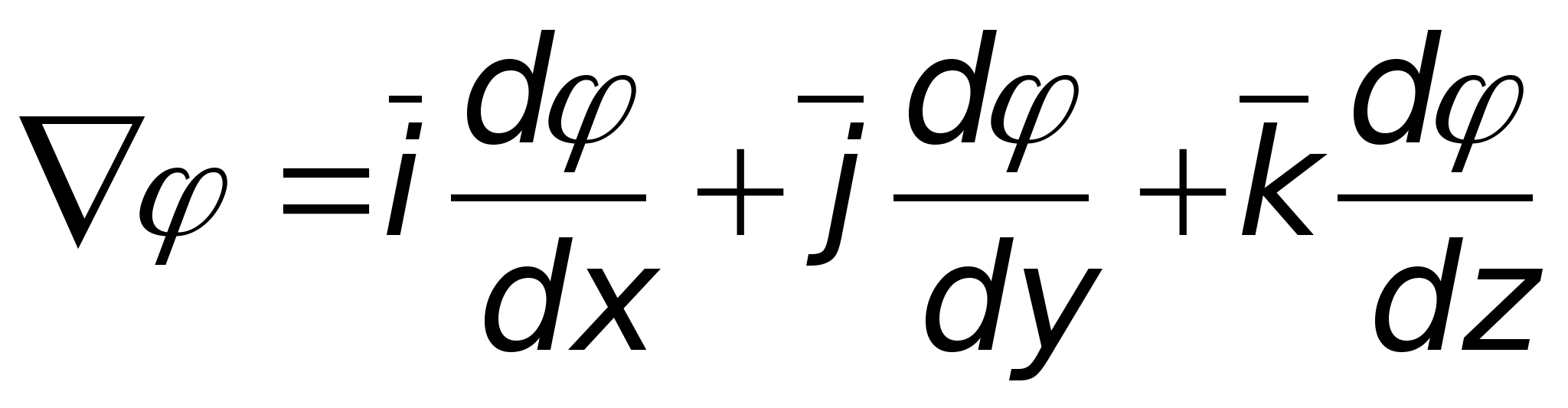 и сравнив его с
и сравнив его с
 ,
видим, что
=
,
видим, что
=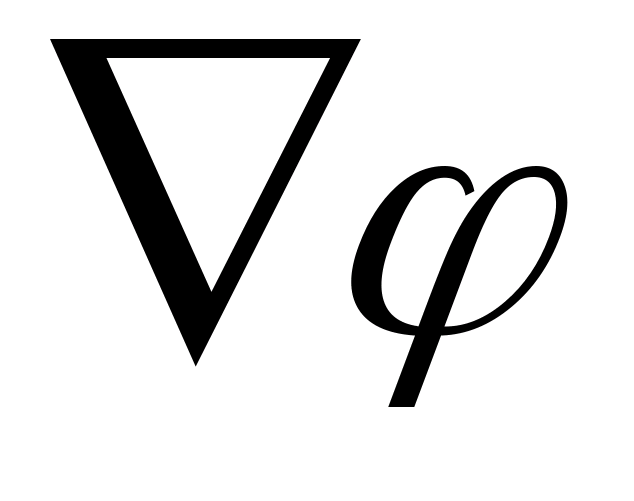 (для скалярной функции частная и полная
производные совпадают). Тогда связь
между напряженностью и потенциалом
может быть записана так:
(для скалярной функции частная и полная
производные совпадают). Тогда связь
между напряженностью и потенциалом
может быть записана так:
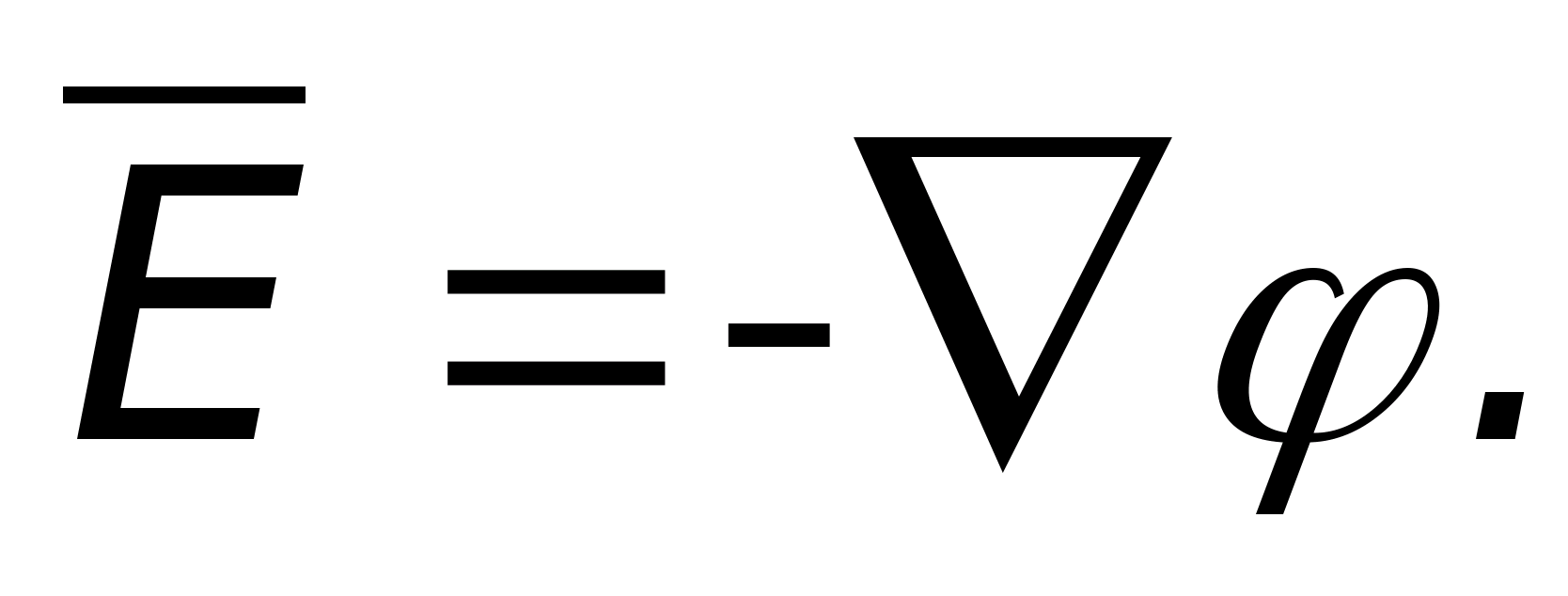
Поляризация вещества
В веществах различают свободные и связанные заряды. Cвободными называются такие заряды, которые под действием сил поля могут свободно перемещаться в веществе, их перемещение не ограничивается внутримолекулярными силами. Под связанными зарядами понимают такие, которые под действием сил поля могут смещаться только в пределах молекулы. Связанные заряды не отделимы от вещества поэтому сумма положительных связанных зарядов равна сумме отрицательных.
Д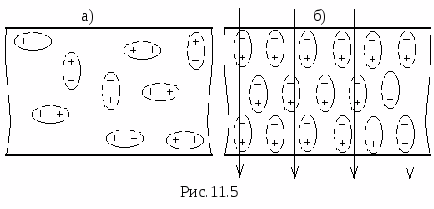
иэлектрические
тела в электростатическом поле
поляризуются. Под поляризацией понимают
упорядоченное изменение расположения
связанных зарядов под действием сил
поля. Наглядно
можно показать поляризацию с помощью
рис.11.5,
на котором изображено тело при отсутствии
электростатического поля и при его
наличии. Если поля нет, то молекулы
(диполи) расположены в хаотическом
беспорядке (рис.11.5,а). В поляризованном
же теле положительные связанные заряды
смещаются в сторону более высокого
потенциала, а отрицательные – в сторону
меньшего (рис.11.5,б), причем смещаются
настолько, что силы воздействия
электрического поля уравновешиваются
внутримолекулярными силами. В результате
поляризации на поверхности вещества
как бы обнажаются положительные или
отрицательные связанные заряды причем
сумма первых из них в точности равна
сумме вторых. Диполи создают свои поля.
В неполяризованном веществе их суммарное
действие равно нулю, а в поляризованном
– нет, оно приводит к ослаблению
результирующего поля и его необходимо
учитывать. С этой целью вводится понятие
электрического момента диполя.
Электрическим моментом двух равных по
величине и противоположных по знаку
зарядов, находящихся друг от друга на
расстоянии l
,
называется произведение
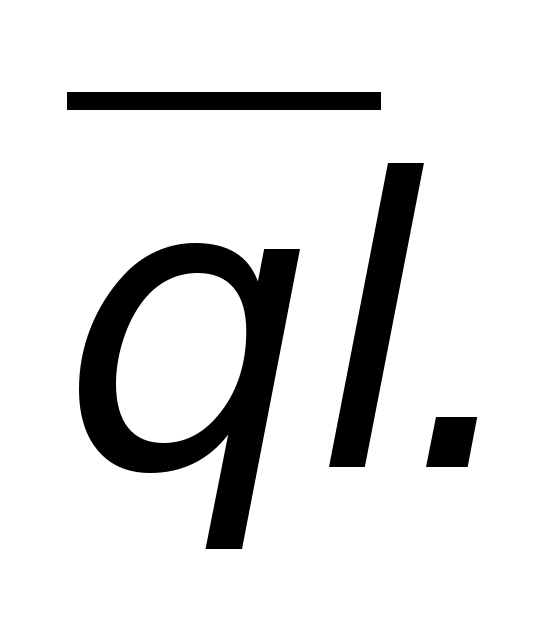 Это вектор, направленный от -q
к
+q
(рис.11.6).
Под действием внешнего
поля диполи вещества стремятся
ориентироваться так, чтобы их электрические
моменты совпадали с напряженностью
внешнего поля. Практическое значение
имеет конечно не один диполь и его
электрический момент (он чрезвычайно
мал), а сумма электрических моментов
диполей, находящихся в единице объёма,
которую принято называть вектором
поляризации
Это вектор, направленный от -q
к
+q
(рис.11.6).
Под действием внешнего
поля диполи вещества стремятся
ориентироваться так, чтобы их электрические
моменты совпадали с напряженностью
внешнего поля. Практическое значение
имеет конечно не один диполь и его
электрический момент (он чрезвычайно
мал), а сумма электрических моментов
диполей, находящихся в единице объёма,
которую принято называть вектором
поляризации
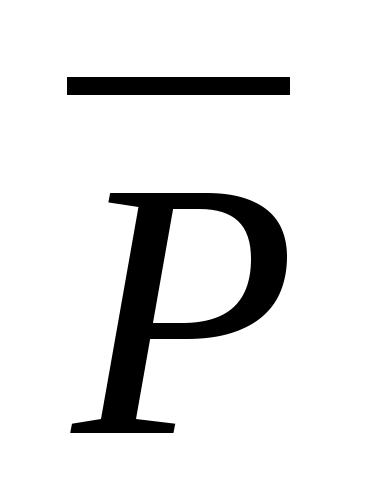 ,
т.е.
,
т.е.
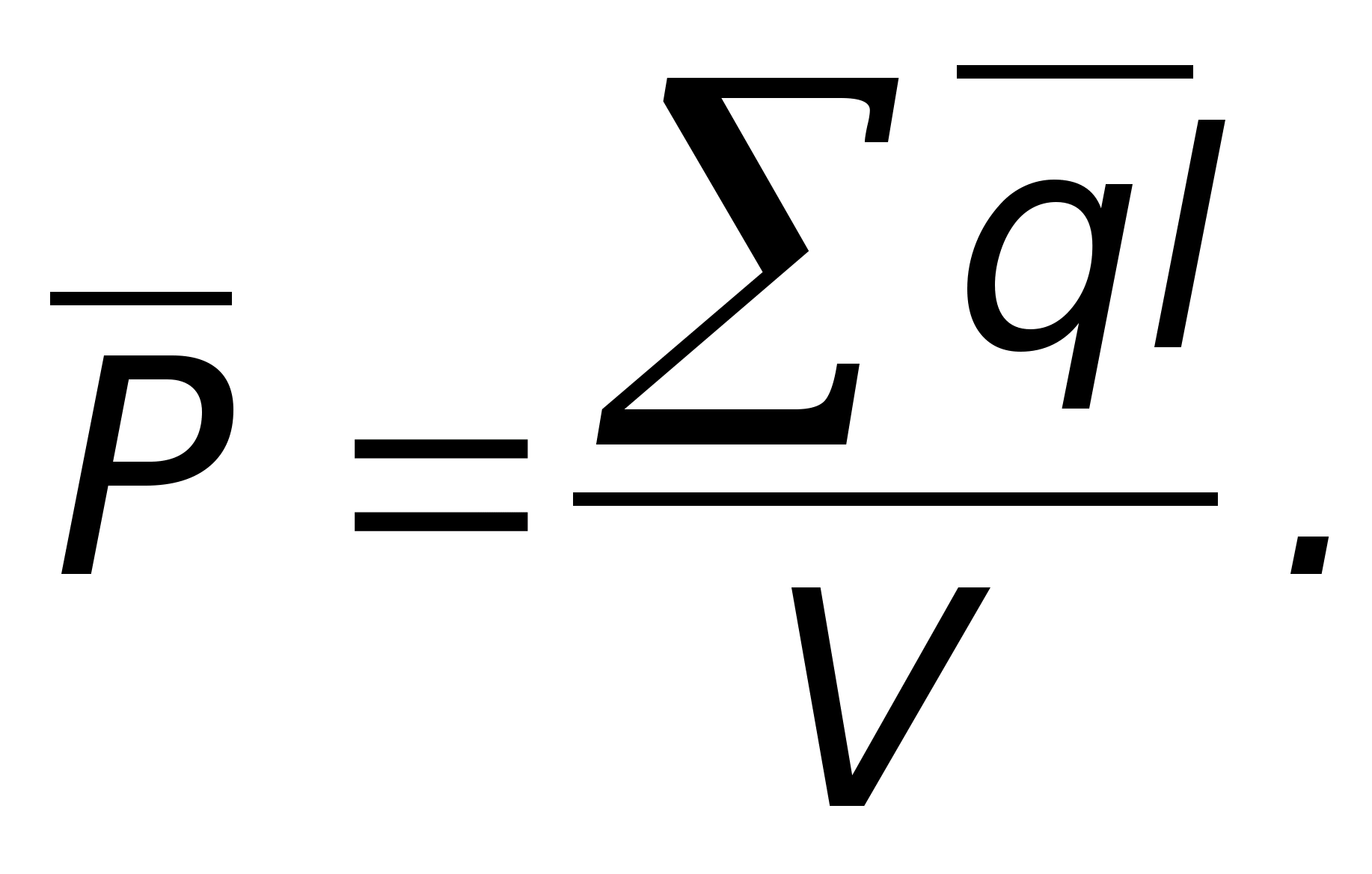 Для
большинства диэлектриков вектор
поляризации пропорционален напряженности
поля
Для
большинства диэлектриков вектор
поляризации пропорционален напряженности
поля
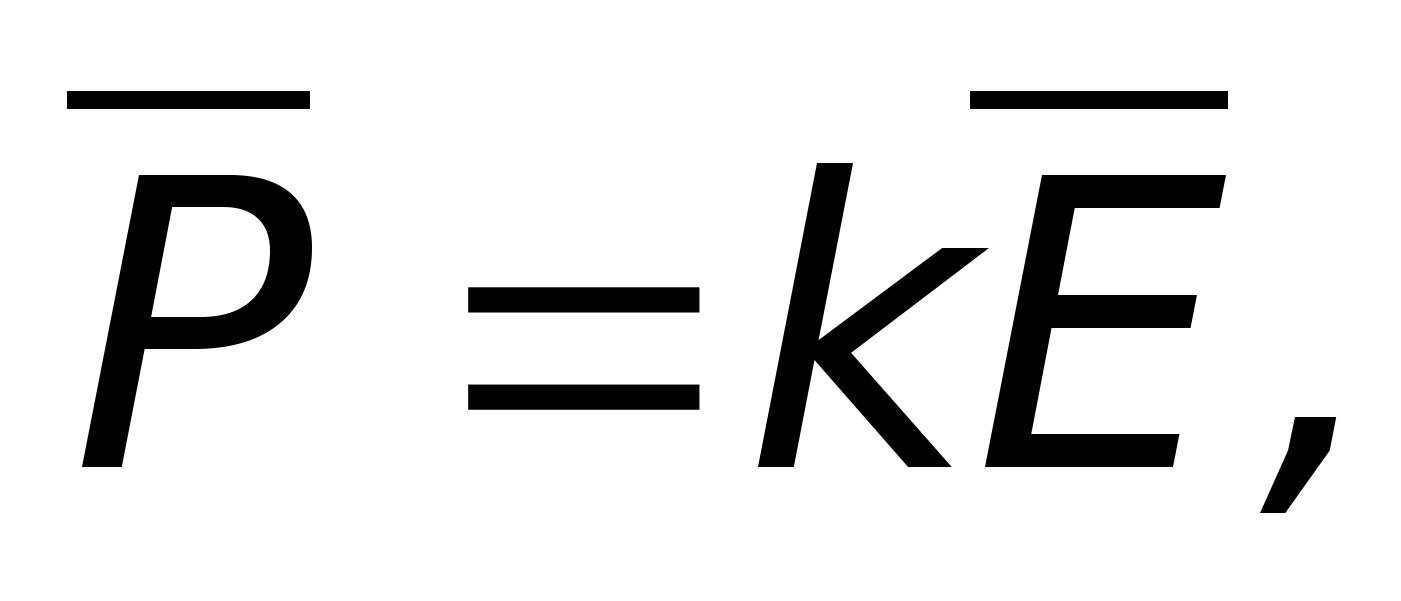 а коэффициент пропорциональности между
ними k
называется электрической
восприимчивостью.
а коэффициент пропорциональности между
ними k
называется электрической
восприимчивостью.
Кроме рассмотренных выше векторных
величин
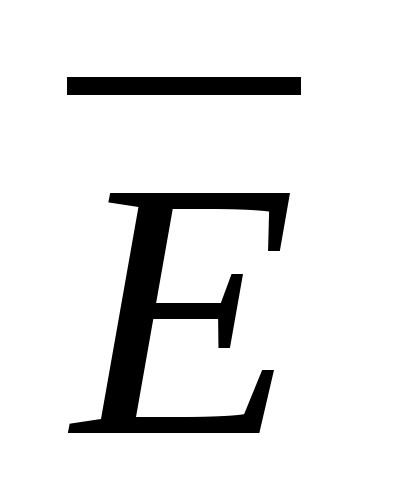 и
,
физический смысл которых мы выяснили,
в теории поля в расчет вводят ещё вектор
и
,
физический смысл которых мы выяснили,
в теории поля в расчет вводят ещё вектор
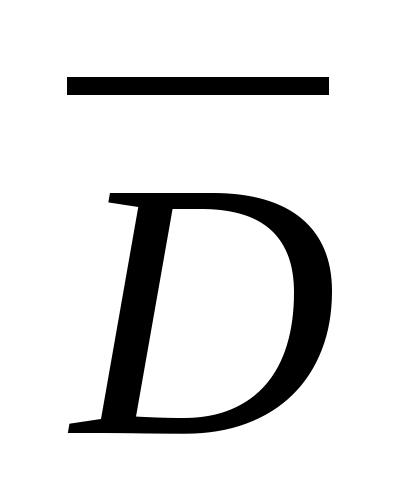 ,
который называется вектором электрического
смещения или вектором электрической
индукции. Он определяется следующим
образом:
где
,
который называется вектором электрического
смещения или вектором электрической
индукции. Он определяется следующим
образом:
где
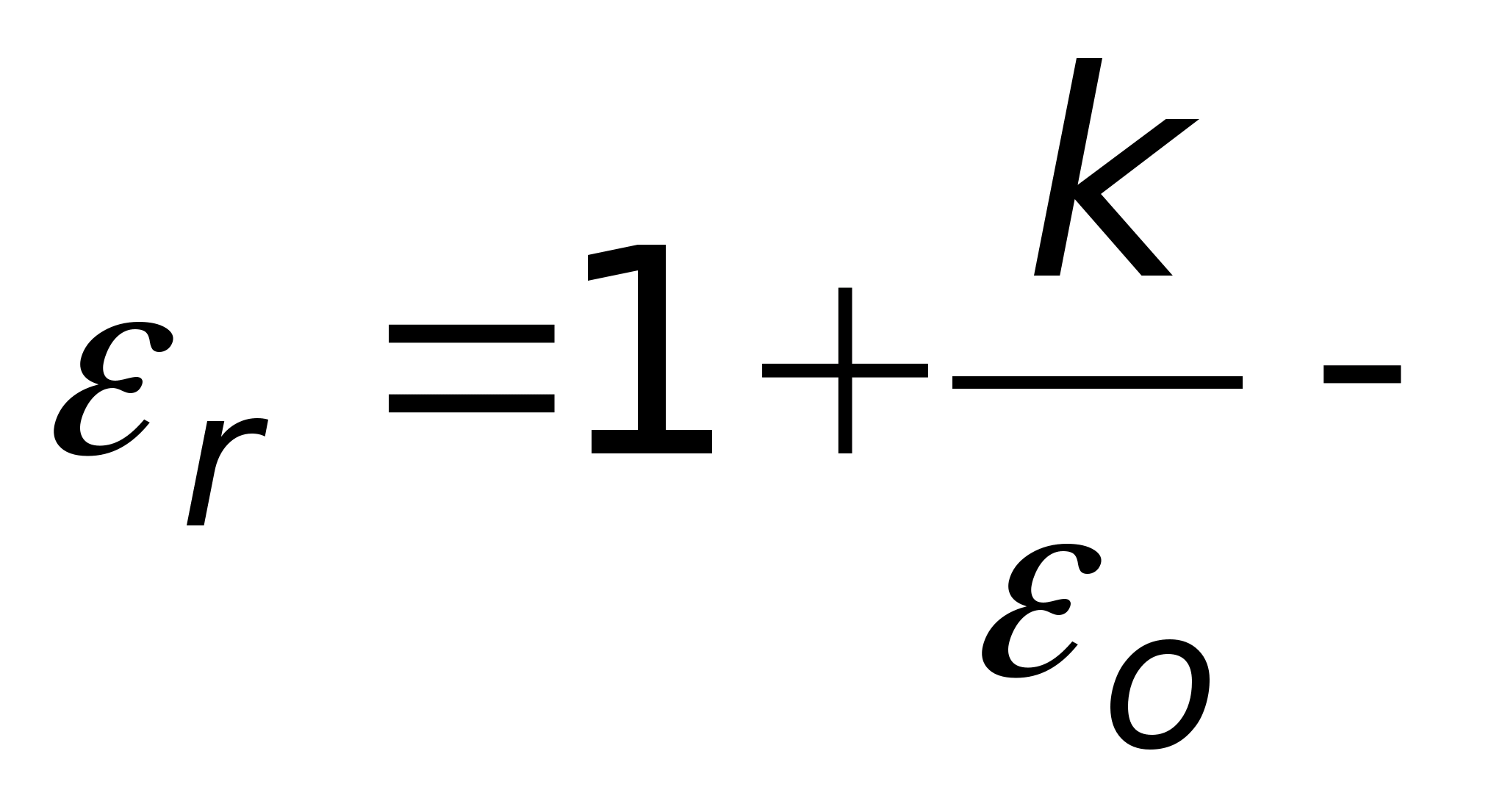 называется относительной диэлектрической
проницаемостью среды, в которой создано
поле, а
называется относительной диэлектрической
проницаемостью среды, в которой создано
поле, а
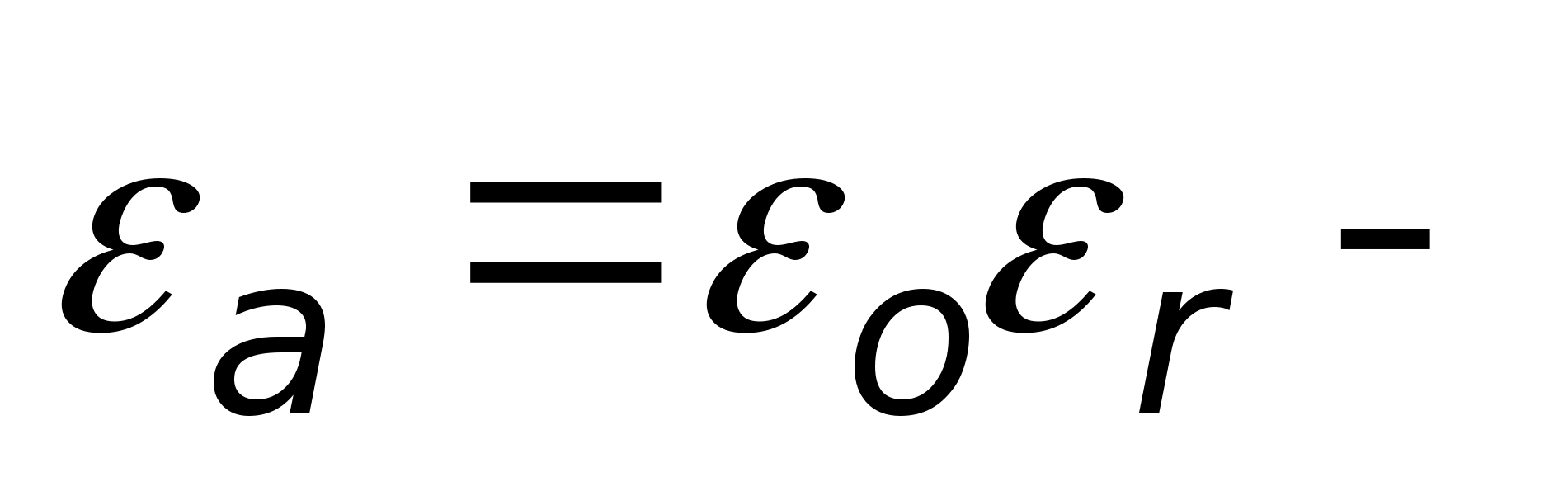 абсолютная диэлектрическая проницаемость
среды, в которой создано поле.
абсолютная диэлектрическая проницаемость
среды, в которой создано поле.
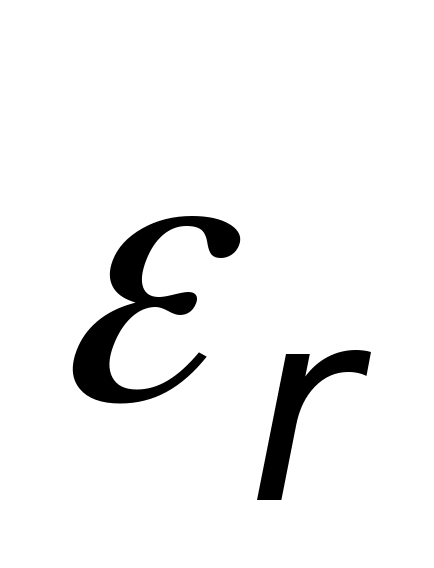 показывает во сколько раз электрические
свойства среды отличаются от свойств
вакуума (это отличие имеет место за счет
поляризации). Для всех сред
определено экспериментальным путем и
приводится в справочниках.
показывает во сколько раз электрические
свойства среды отличаются от свойств
вакуума (это отличие имеет место за счет
поляризации). Для всех сред
определено экспериментальным путем и
приводится в справочниках.
Теорема Гаусса
Теорема Гаусса представляет
собой основной закон электростатического
поля. Он обнаружен экспериментальным
путем и математически записывается так
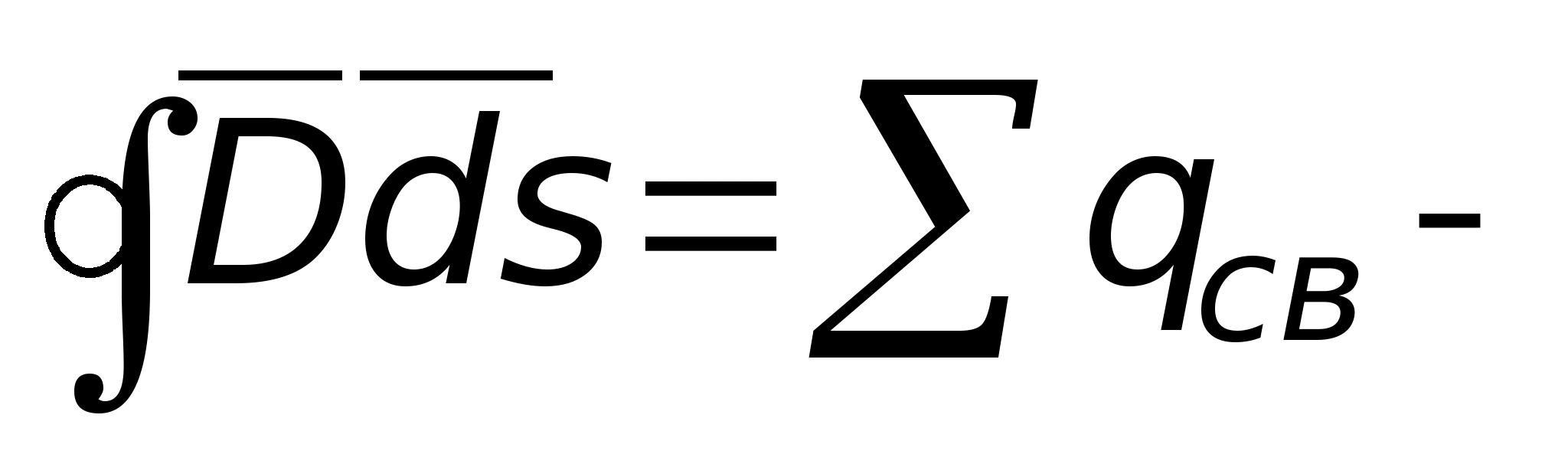 поток вектора электрического смещения
через любую замкнутую поверхность,
окружающую некоторый объём, равен
алгебраической сумме свободных зарядов,
находящихся внутри этой поверхности
(в сумме
поток вектора электрического смещения
через любую замкнутую поверхность,
окружающую некоторый объём, равен
алгебраической сумме свободных зарядов,
находящихся внутри этой поверхности
(в сумме
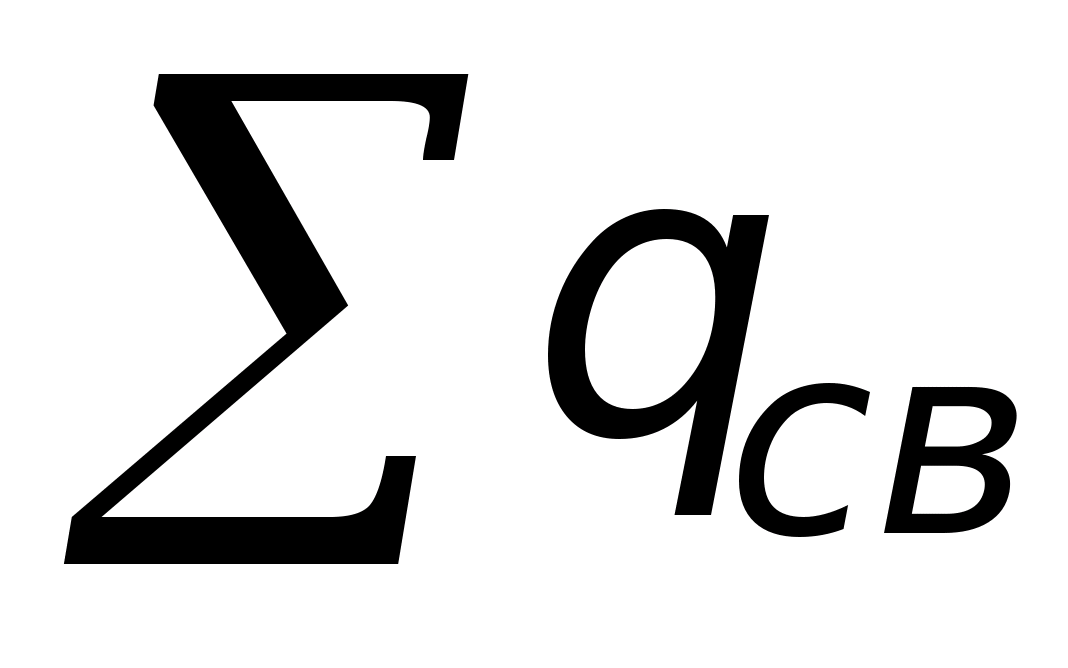 заряды
берутся со своими знаками). Поскольку
заряды
берутся со своими знаками). Поскольку
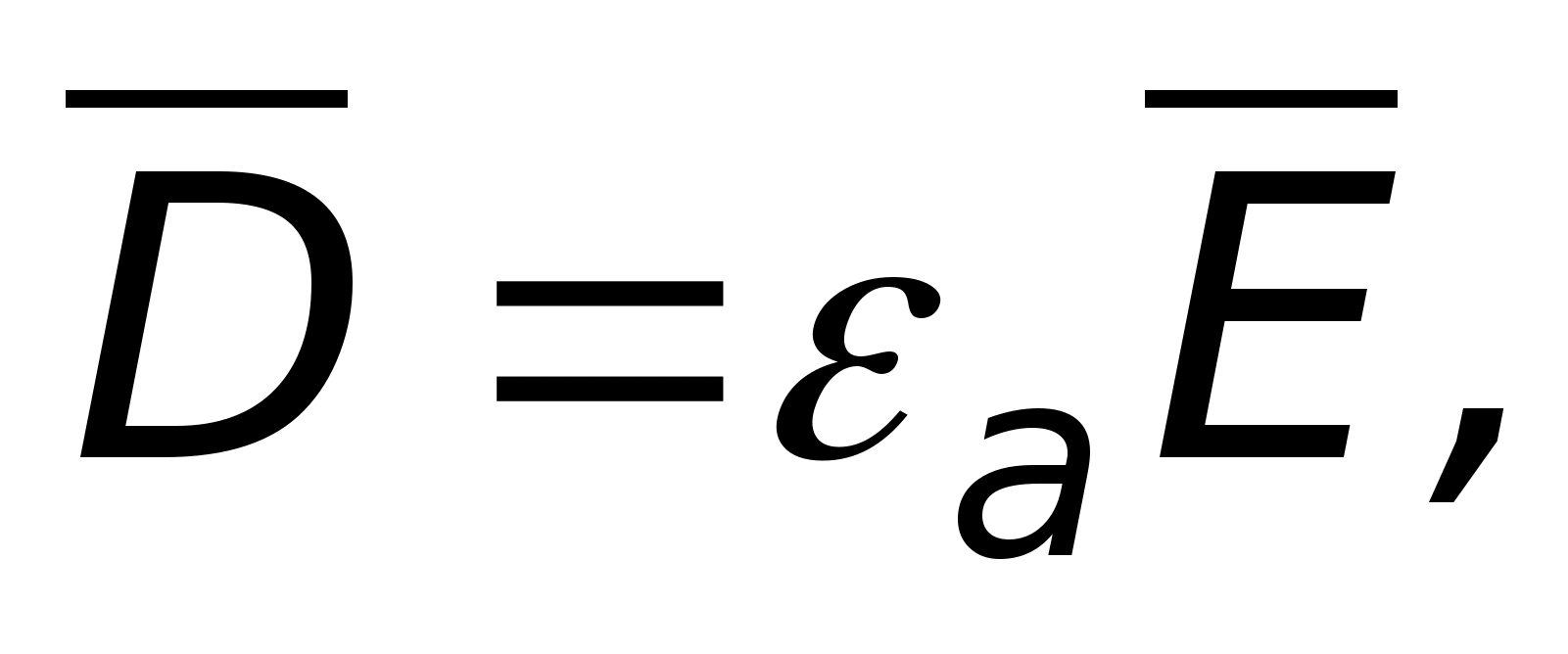 то
то
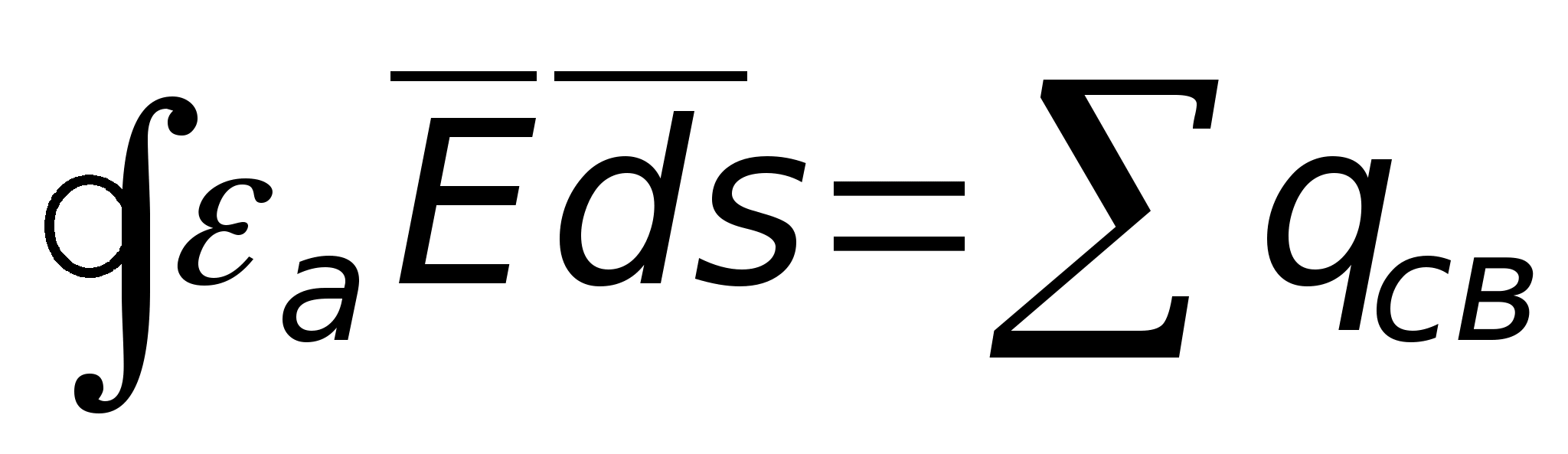 .
Для однородных и изотропных сред
.
Для однородных и изотропных сред
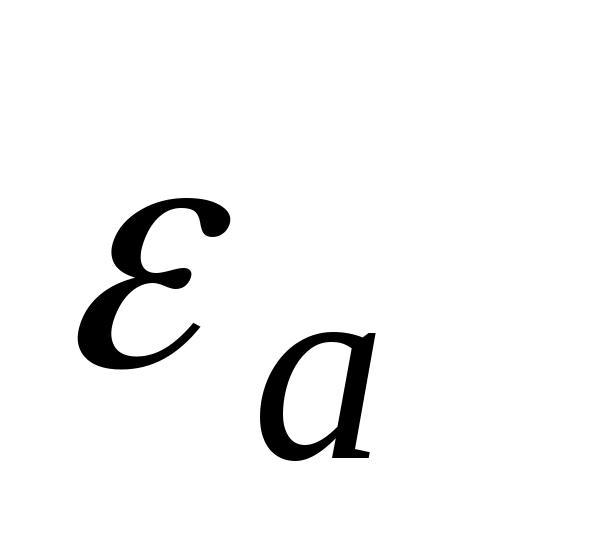 является
постоянной величиной и её можно вынести
за знак интеграла, тогда
является
постоянной величиной и её можно вынести
за знак интеграла, тогда
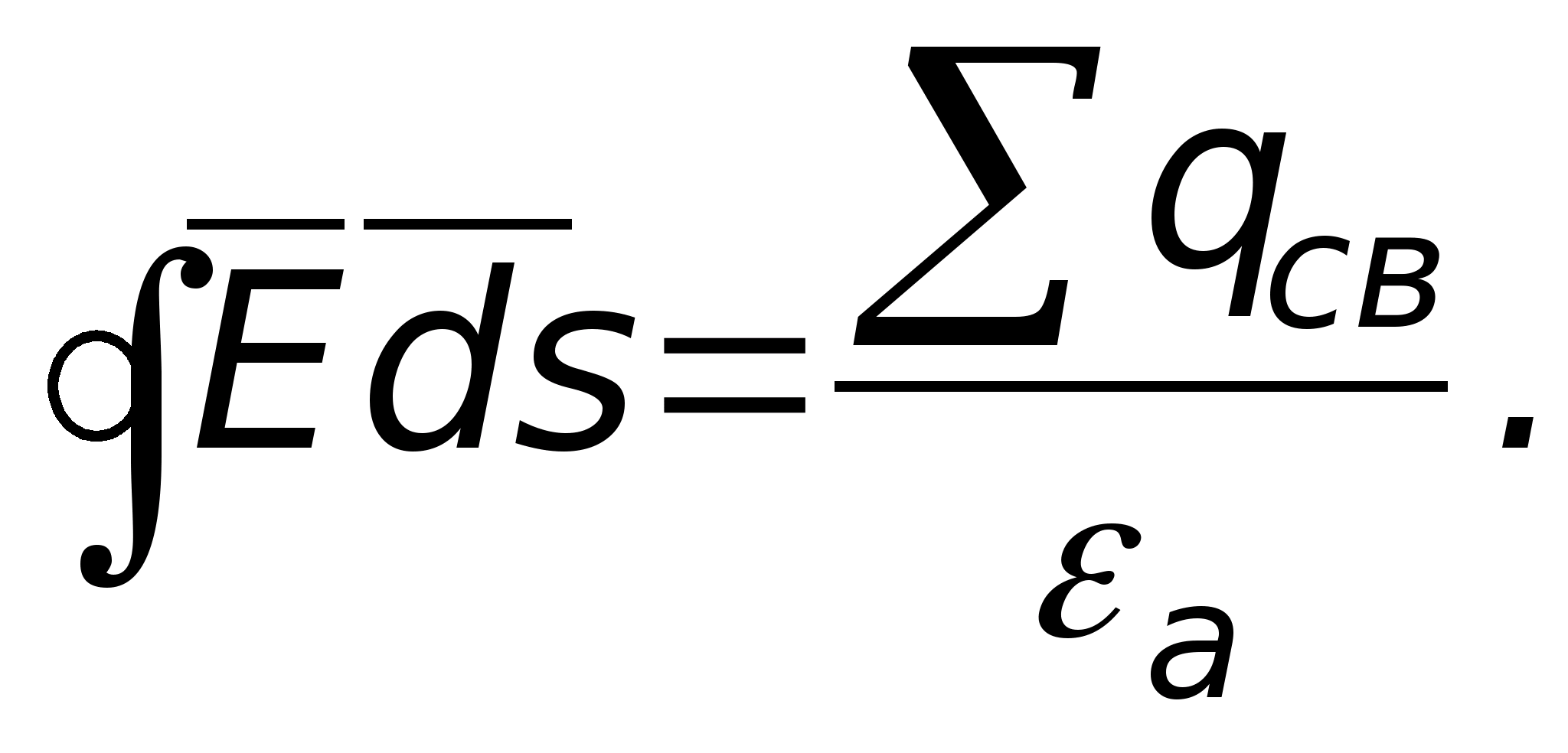 Интересно, что поток вектора D
или Е
зависит только от
и не зависит от расположения зарядов
внутри замкнутой поверхности. Поток
вектора Е
создается не только свободными, но и
связанными зарядами. Последние можно
учитывать не через
,
а через отдельно взятую сумму связанных
зарядов и тогда формула теоремы Гаусса
выглядит так:
Интересно, что поток вектора D
или Е
зависит только от
и не зависит от расположения зарядов
внутри замкнутой поверхности. Поток
вектора Е
создается не только свободными, но и
связанными зарядами. Последние можно
учитывать не через
,
а через отдельно взятую сумму связанных
зарядов и тогда формула теоремы Гаусса
выглядит так:
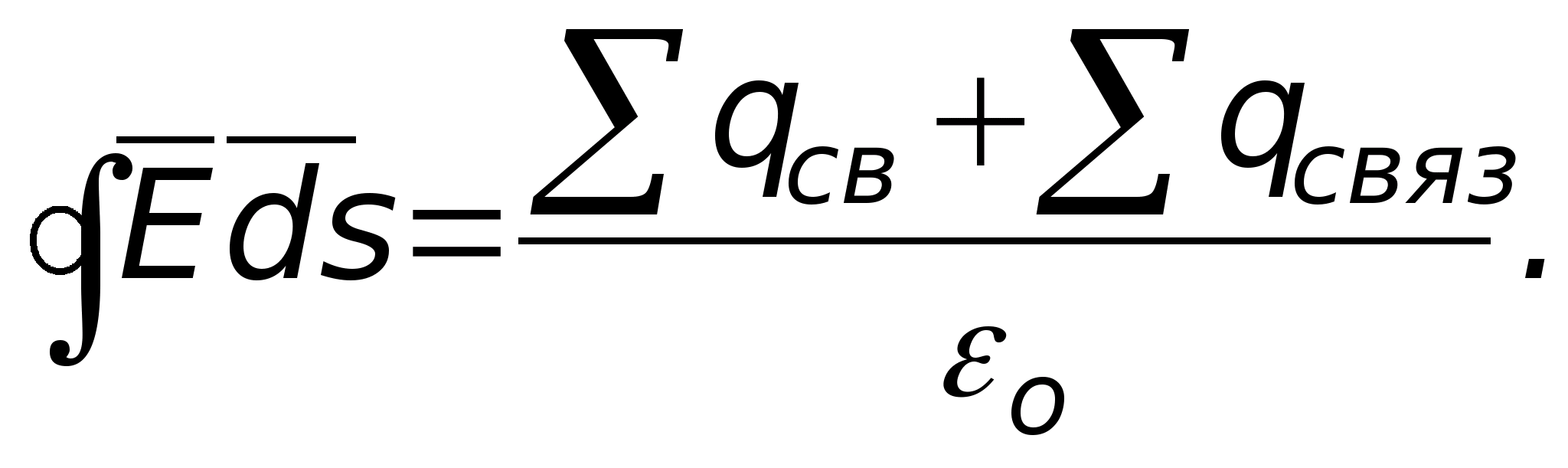 Эти три формулы представляют собой
интегральную форму записи теоремы
Гаусса, которая с большой эффективностью
и простотой может быть использована
для расчета напряженности поля в
какой-либо точке, если через неё можно
провести замкнутую поверхность, все
точки которой находятся в одинаковых
условиях по отношению к зарядам, создающим
поле. В качестве примера рассчитаем
поле, создаваемое точечным зарядом.
Эти три формулы представляют собой
интегральную форму записи теоремы
Гаусса, которая с большой эффективностью
и простотой может быть использована
для расчета напряженности поля в
какой-либо точке, если через неё можно
провести замкнутую поверхность, все
точки которой находятся в одинаковых
условиях по отношению к зарядам, создающим
поле. В качестве примера рассчитаем
поле, создаваемое точечным зарядом.
Т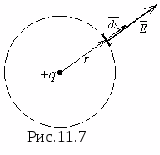 очечным
называется заряд, расположенный на теле
очень малых геометрических размеров.
На рис.11.7 он изобразится в виде точки
(отсюда и название). Допустим, что этот
заряд является положительным и расположен
в среде с проницаемостью
очечным
называется заряд, расположенный на теле
очень малых геометрических размеров.
На рис.11.7 он изобразится в виде точки
(отсюда и название). Допустим, что этот
заряд является положительным и расположен
в среде с проницаемостью
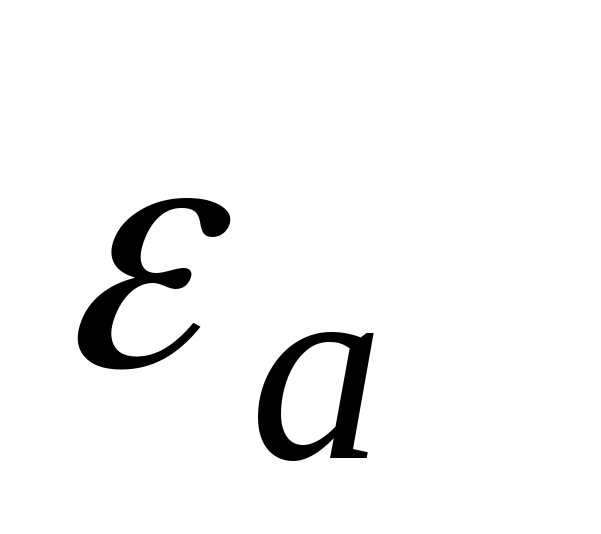 .
Возьмём произвольную точку, отстоящую
на расстояние r
от точечного заряда.
Напряженность в этой точке будет
направлена по радиальной линии (см.
рис.11.7). Для её расчета применим формулу
С этой целью проведём через данную точку
замкнутую сферическую поверхность с
центром, совпадающим с точечным зарядом.
Вектор элементарной поверхности
.
Возьмём произвольную точку, отстоящую
на расстояние r
от точечного заряда.
Напряженность в этой точке будет
направлена по радиальной линии (см.
рис.11.7). Для её расчета применим формулу
С этой целью проведём через данную точку
замкнутую сферическую поверхность с
центром, совпадающим с точечным зарядом.
Вектор элементарной поверхности
 направляется в сторону внешней нормали
к площадке (она расположена в окрестности
рассматриваемой точки). Поскольку в
нашем примере векторы Е
и ds
совпадают, то их
произведение совпадает с произведением
модулей. Кроме того во всех точках
рассматриваемой сферы величина вектора
Е
одинакова
в силу симметрии. С учётом сказанного
имеем:
поскольку поверхность сферы равна
направляется в сторону внешней нормали
к площадке (она расположена в окрестности
рассматриваемой точки). Поскольку в
нашем примере векторы Е
и ds
совпадают, то их
произведение совпадает с произведением
модулей. Кроме того во всех точках
рассматриваемой сферы величина вектора
Е
одинакова
в силу симметрии. С учётом сказанного
имеем:
поскольку поверхность сферы равна
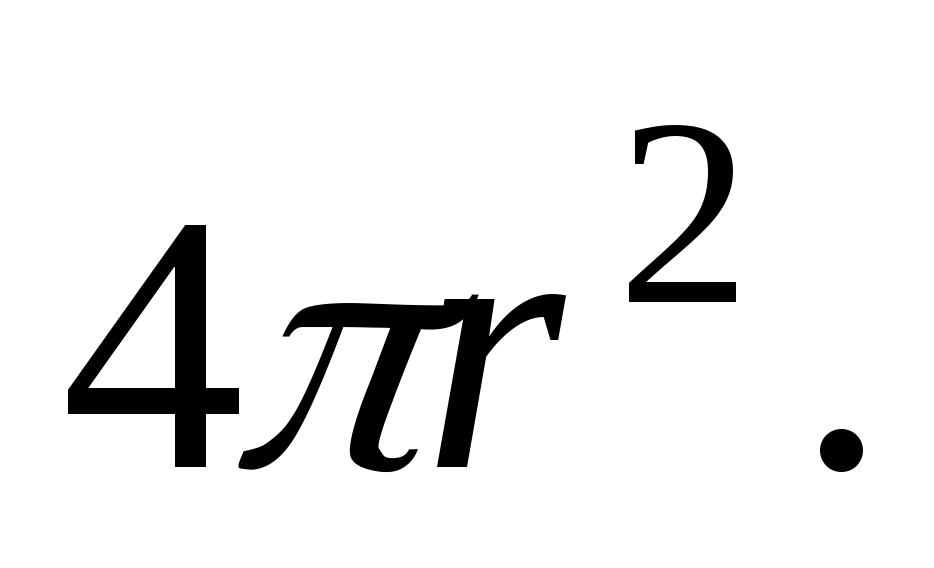 Сумма свободных зарядов равна только
заданному точечному заряду
Сумма свободных зарядов равна только
заданному точечному заряду
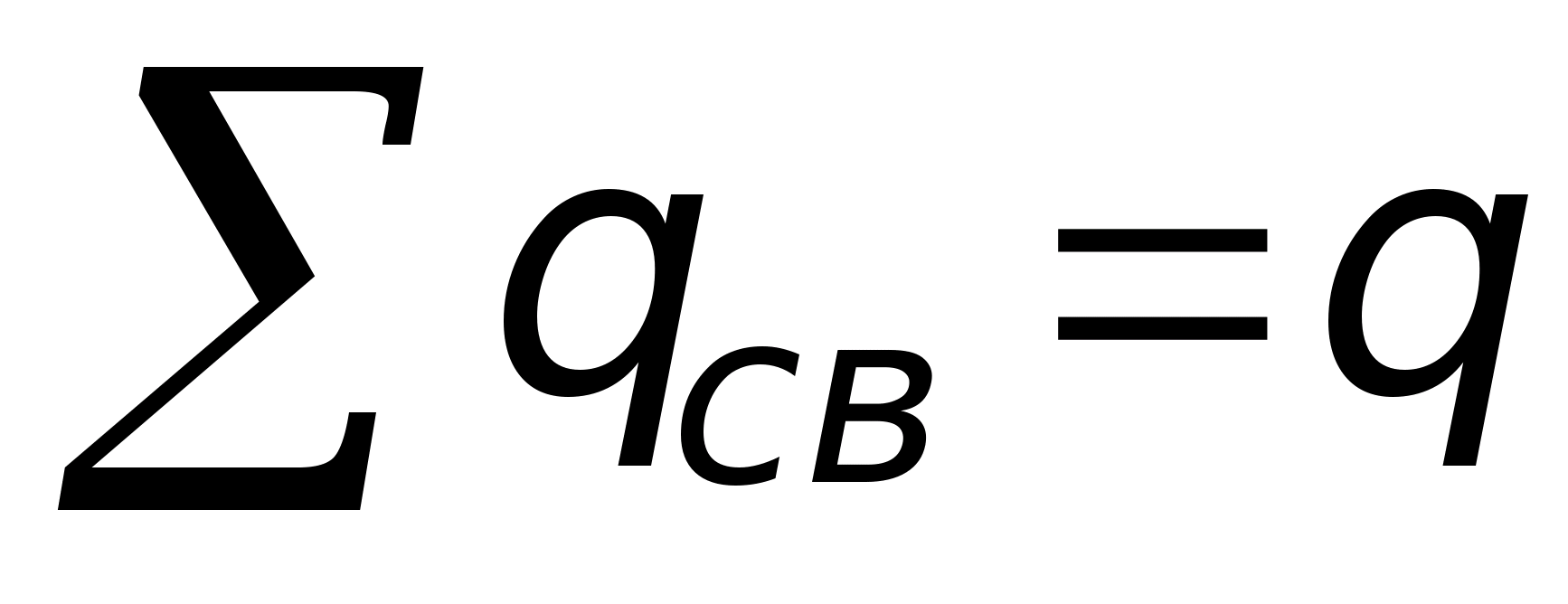 .
Подставляя эти значения в формулу
теоремы Гаусса, получаем:
.
Подставляя эти значения в формулу
теоремы Гаусса, получаем:
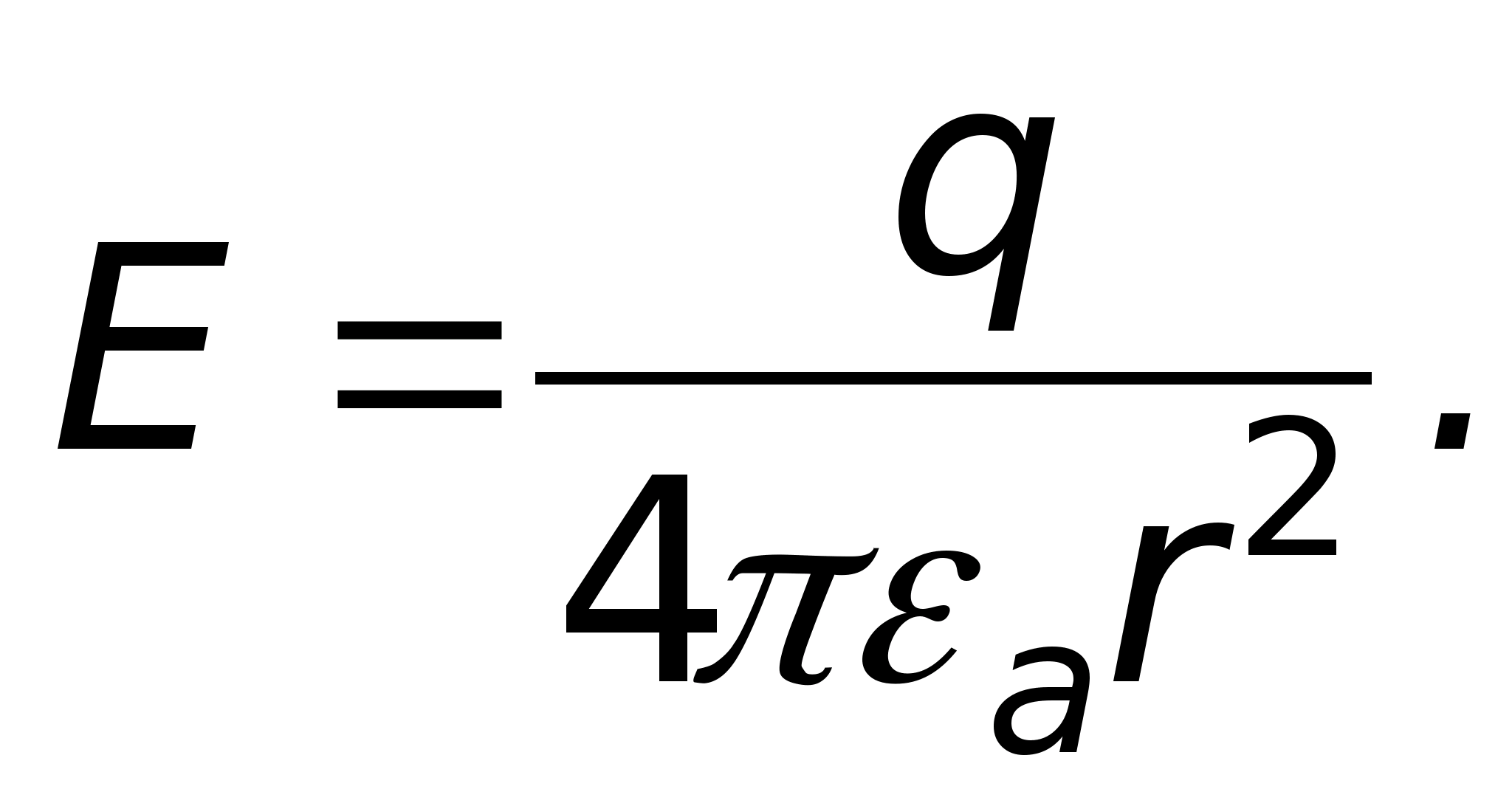 Таким образом, в данном поле напряженность
изменяется обратно пропорционально
r
2 .
Таким образом, в данном поле напряженность
изменяется обратно пропорционально
r
2 .
Произведём расчет потенциала в
данном поле, исходя из формулы
.
Если учесть, что напряженность, а значит
и потенциал, зависят только от радиуса,
то последняя формула перепишется так
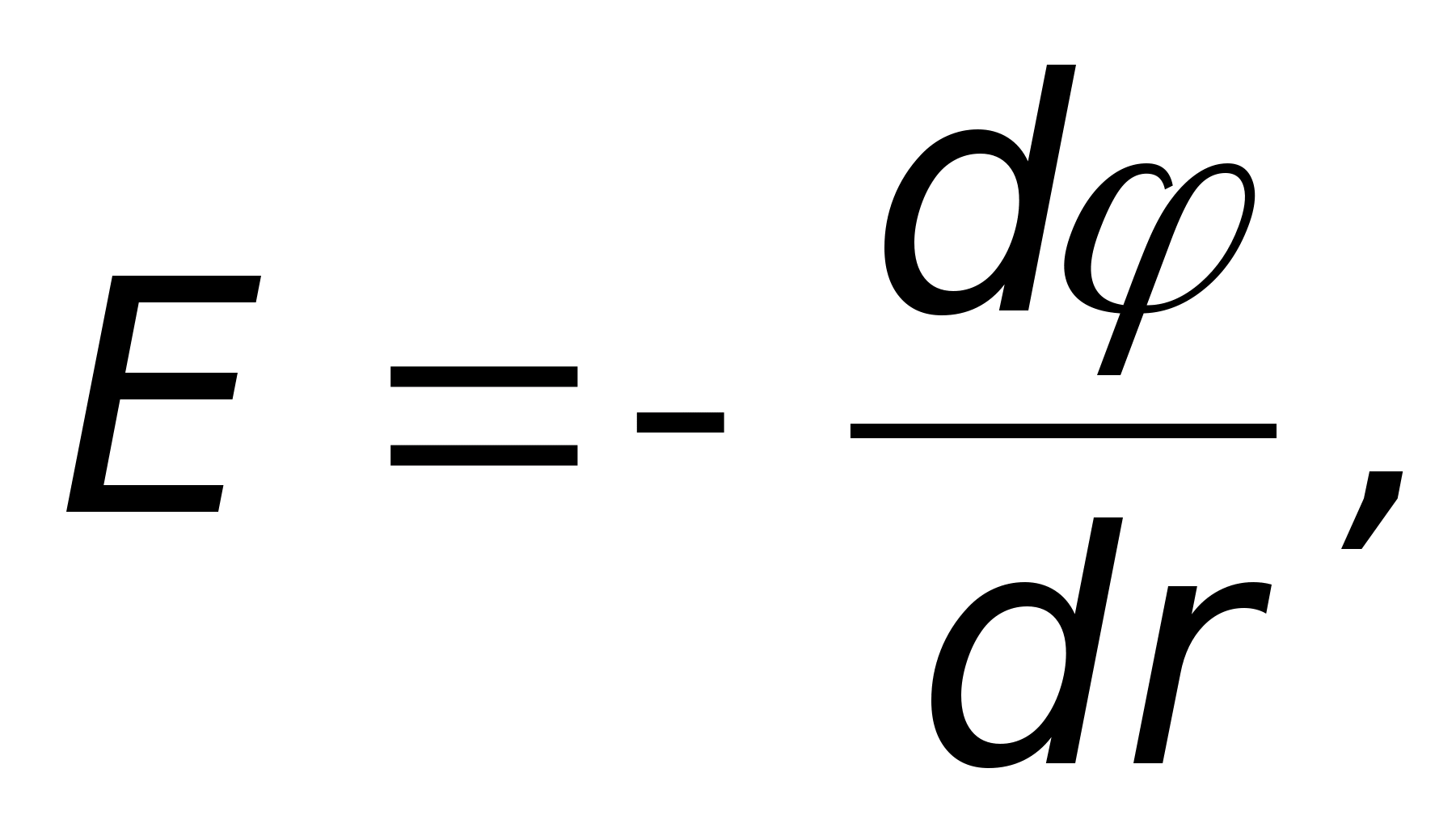 откуда
откуда
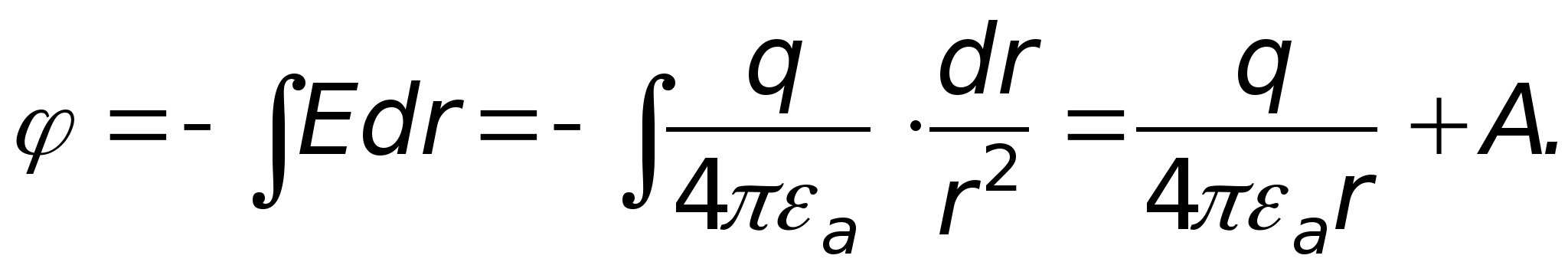 Отсюда следует, что потенциал в данном
поле изменяется обратно
пропорционально r
.
Постоянная интегрирования А зависит
от того, где расположить точку с нулевым
потенциалом.
Отсюда следует, что потенциал в данном
поле изменяется обратно
пропорционально r
.
Постоянная интегрирования А зависит
от того, где расположить точку с нулевым
потенциалом.
Интегральная форма записи теоремы
Гаусса не даёт ответа на вопрос о том,
как связана напряженность поля в данной
точке с зарядом в этой же точке. Ответ
на этот вопрос даёт дифференциальная
форма этой теоремы, которая вытекает
из интегральной.
Для этого выражение
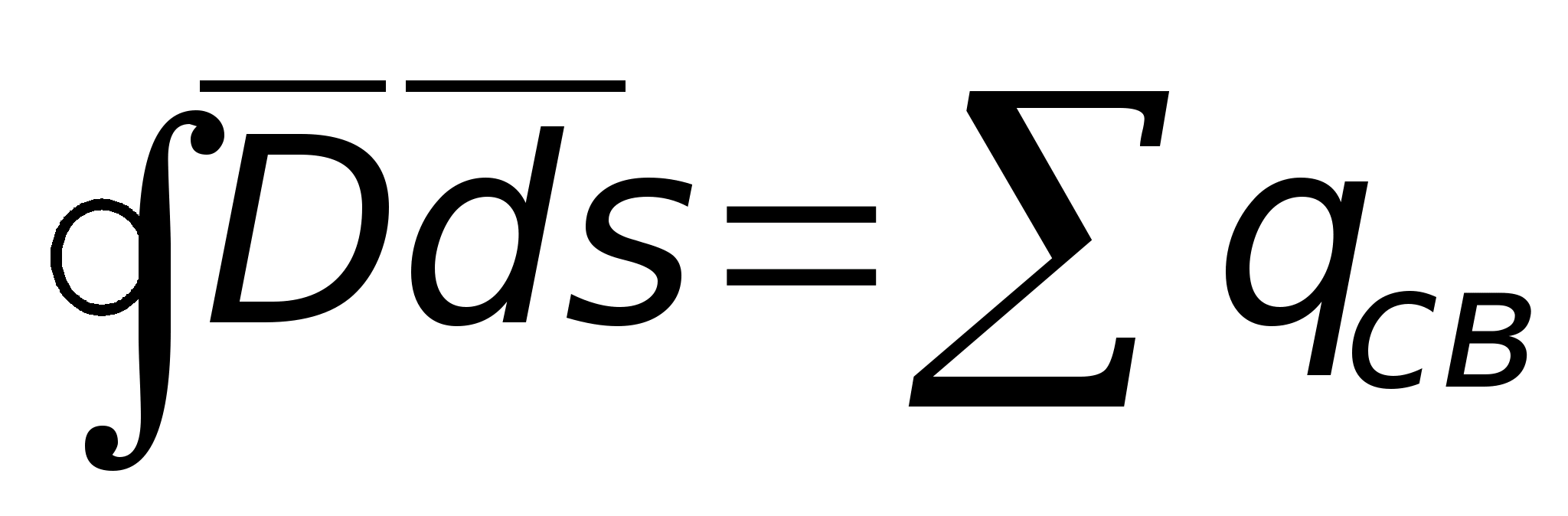 поделим на величину объёма, ограниченного
поверхностью интегрирования
поделим на величину объёма, ограниченного
поверхностью интегрирования
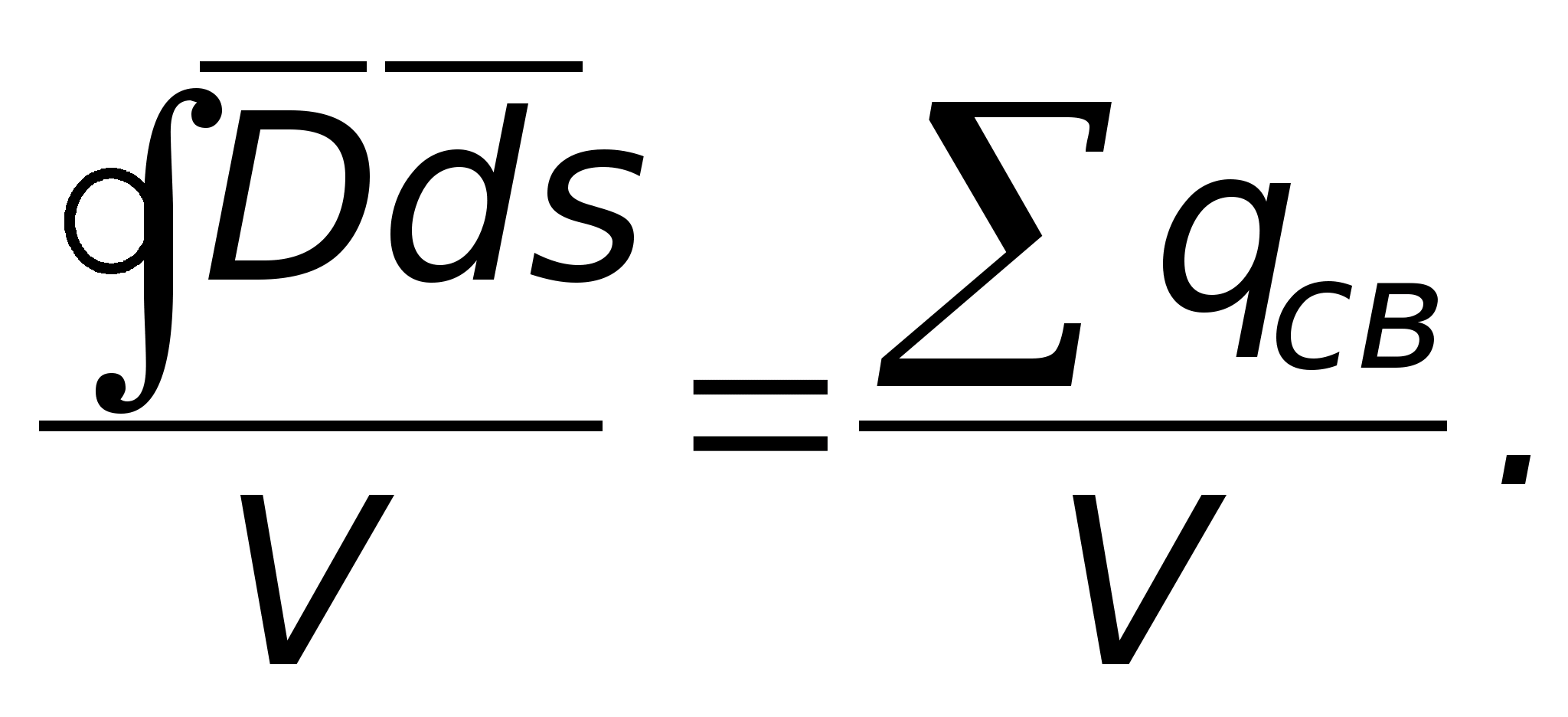 Это соотношение справедливо для объёма
любой величины. Устремим его к нулю
(говорят, что стянем поверхность в
точку). Тогда
Это соотношение справедливо для объёма
любой величины. Устремим его к нулю
(говорят, что стянем поверхность в
точку). Тогда
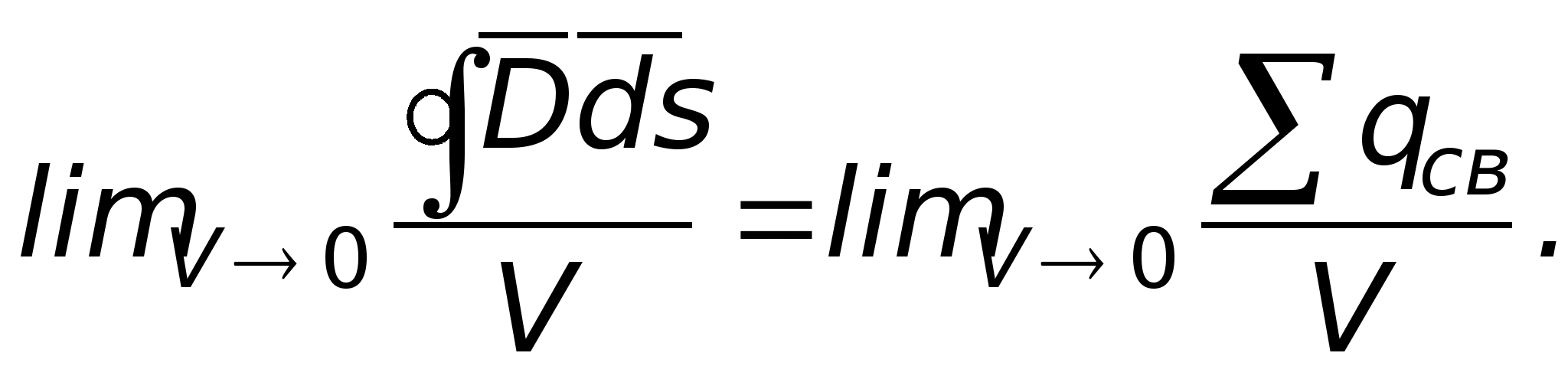 Предел отношения потока вектора D
через замкнутую поверхность, ограничивающую
некоторый объём, к величине этого объёма
называется дивергенцией вектора D
(
Предел отношения потока вектора D
через замкнутую поверхность, ограничивающую
некоторый объём, к величине этого объёма
называется дивергенцией вектора D
(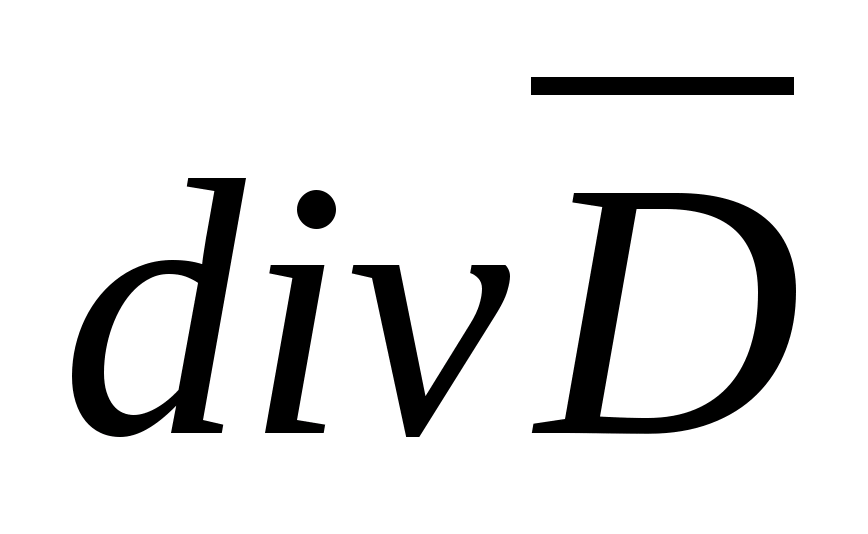 )
или истоком, или расхождением. В правой
части последнего равенства стоит
объёмная плотность свободного заряда
ρ
св
.
Тогда
)
или истоком, или расхождением. В правой
части последнего равенства стоит
объёмная плотность свободного заряда
ρ
св
.
Тогда
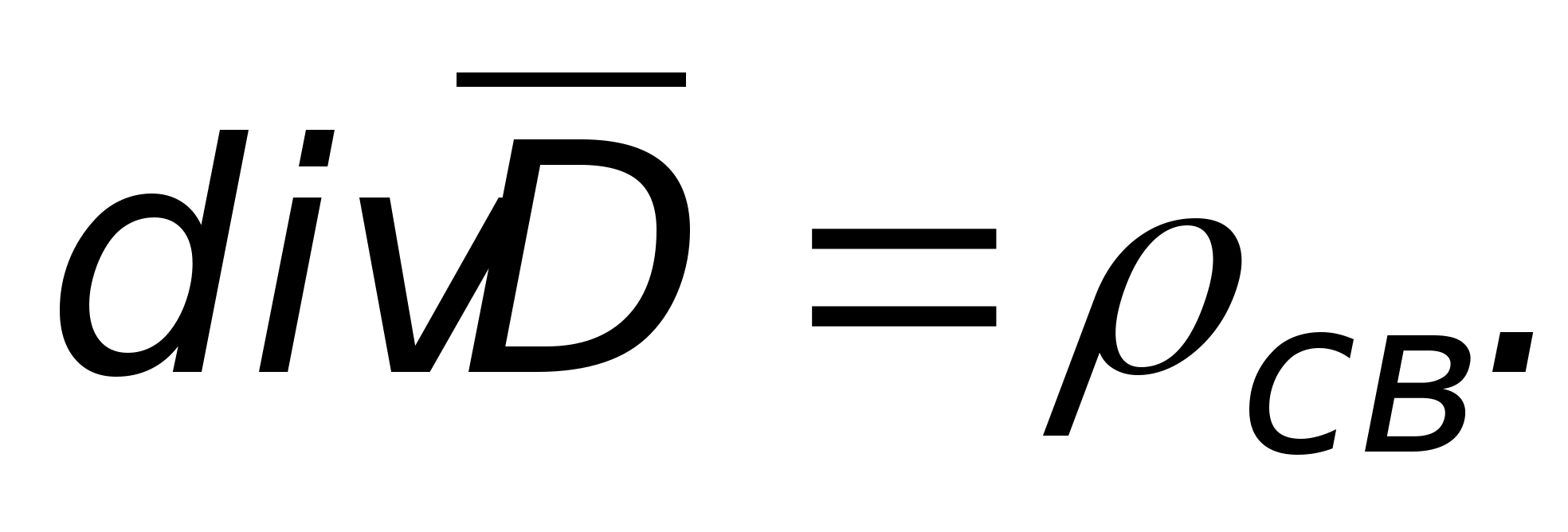 Это и есть теорема Гаусса в дифференциальной
форме. Её суть поясним с помощью трех
случаев, о
Это и есть теорема Гаусса в дифференциальной
форме. Её суть поясним с помощью трех
случаев, о![]() траженных
на рис.11.8. Если в рассматриваемой точке
поля объёмная плотность свободного
заряда положительна, то из бесконечно
малого объёма, окружающего данную точку,
линии вектора D
исходят (исток положительный, расхождение
положительное, дивергенция положительная).
Если в рассматриваемой точке поля
объёмная плотность свободного заряда
отрицательная, то в бесконечно малый
объём, окружающий данную точку, линии
вектора D
входят (исток отрицательный, расхождение
отрицательное, дивергенция отрицательная).
И, наконец, если в рассматриваемой точке
нет свободного заряда, то в такой точке
нет ни стока ни истока линий вектора D
,
т.е. в такой точке лини
вектора D
не начинаются и не заканчиваются, а
пронизывают бесконечно малый объём,
окружающий данную точку.
траженных
на рис.11.8. Если в рассматриваемой точке
поля объёмная плотность свободного
заряда положительна, то из бесконечно
малого объёма, окружающего данную точку,
линии вектора D
исходят (исток положительный, расхождение
положительное, дивергенция положительная).
Если в рассматриваемой точке поля
объёмная плотность свободного заряда
отрицательная, то в бесконечно малый
объём, окружающий данную точку, линии
вектора D
входят (исток отрицательный, расхождение
отрицательное, дивергенция отрицательная).
И, наконец, если в рассматриваемой точке
нет свободного заряда, то в такой точке
нет ни стока ни истока линий вектора D
,
т.е. в такой точке лини
вектора D
не начинаются и не заканчиваются, а
пронизывают бесконечно малый объём,
окружающий данную точку.
Поскольку
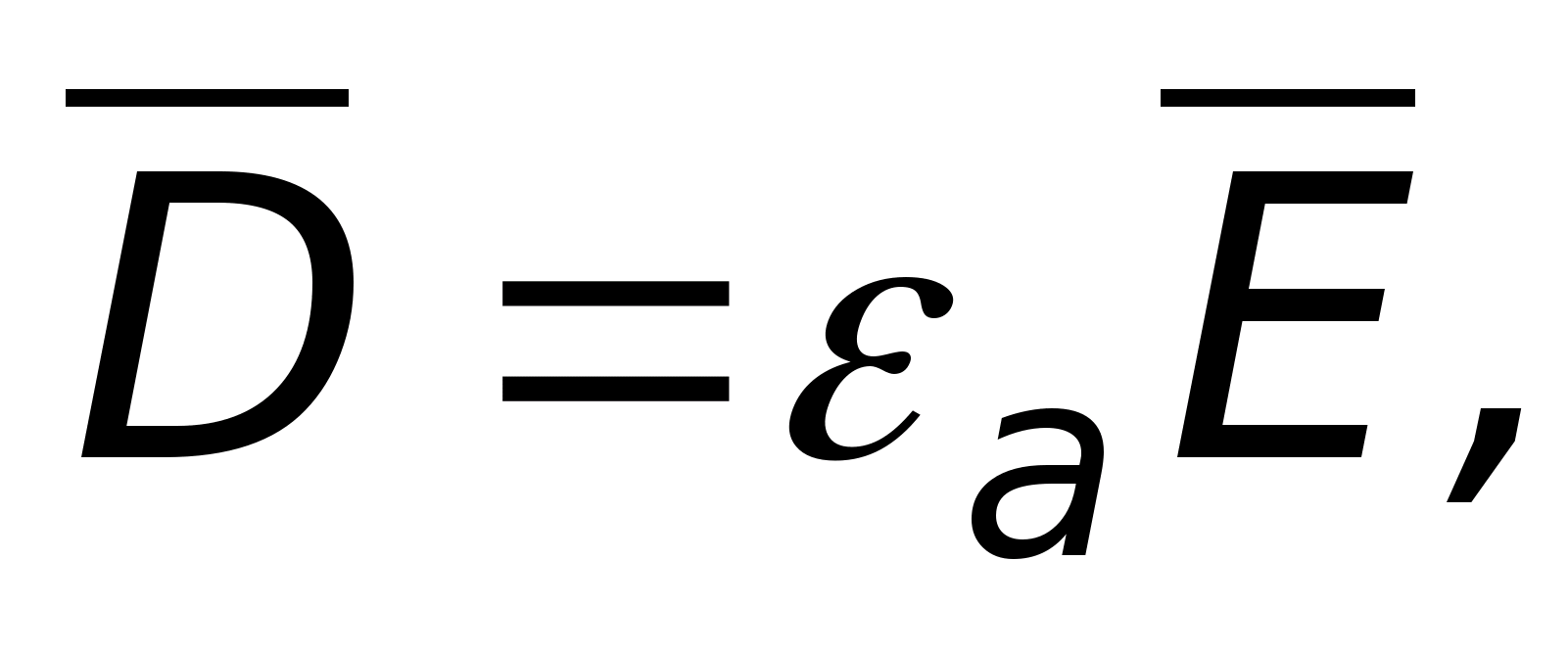 то
то
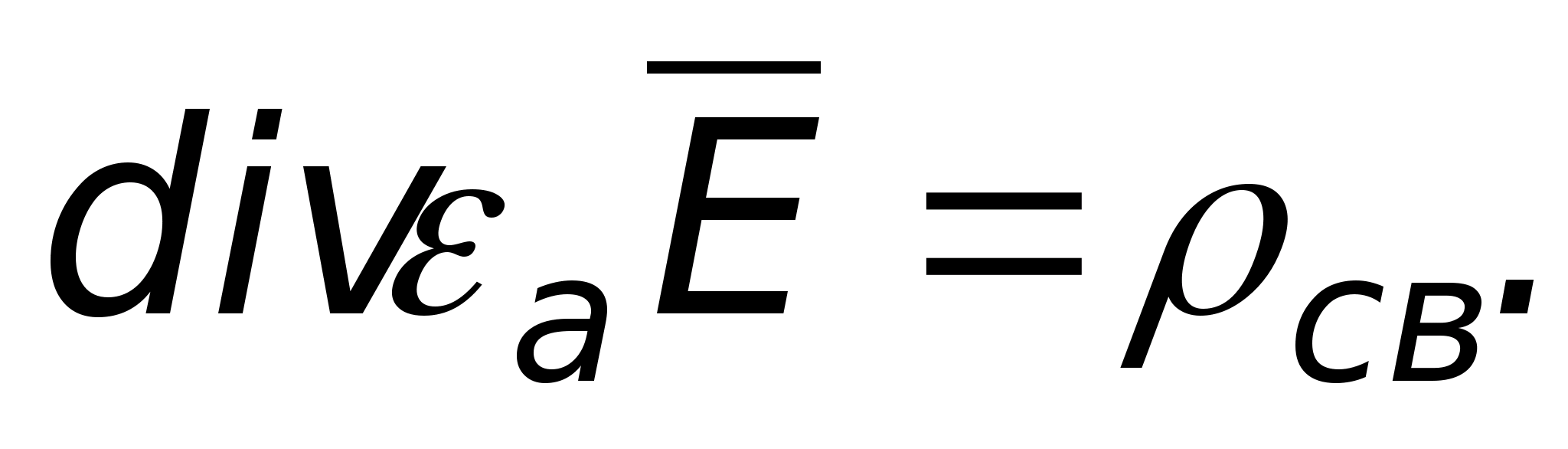 Для однородных и изотропных сред
Для однородных и изотропных сред
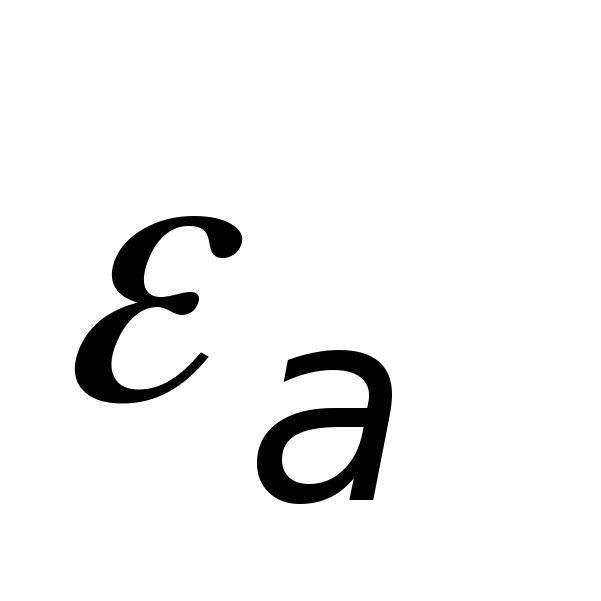 является
постоянной величиной и её можно вынести
за знак div
,
тогда получим:
является
постоянной величиной и её можно вынести
за знак div
,
тогда получим:
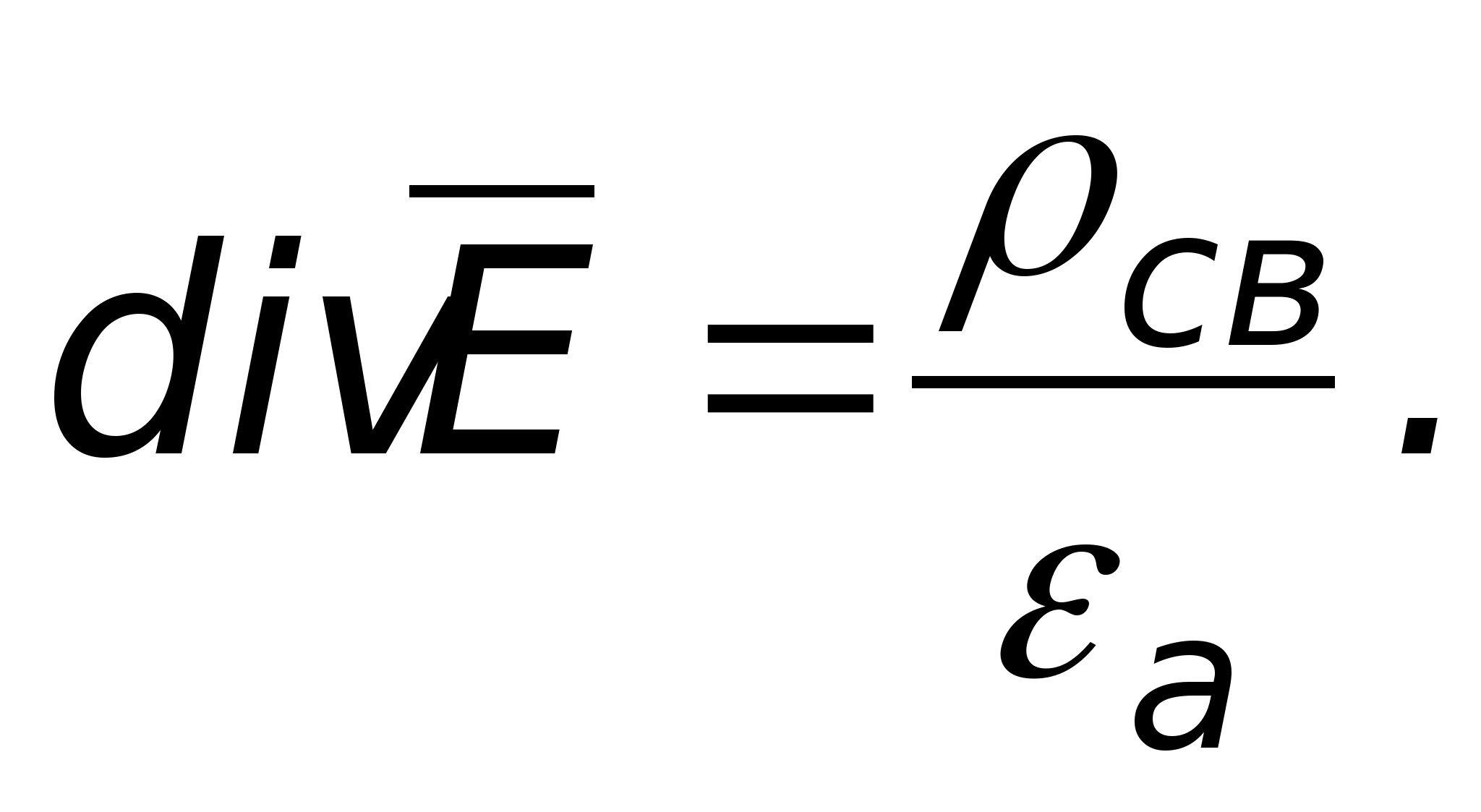 Если явление поляризации учитывать с
помощью связанных зарядов, то последнее
выражение можно так переписать
Если явление поляризации учитывать с
помощью связанных зарядов, то последнее
выражение можно так переписать
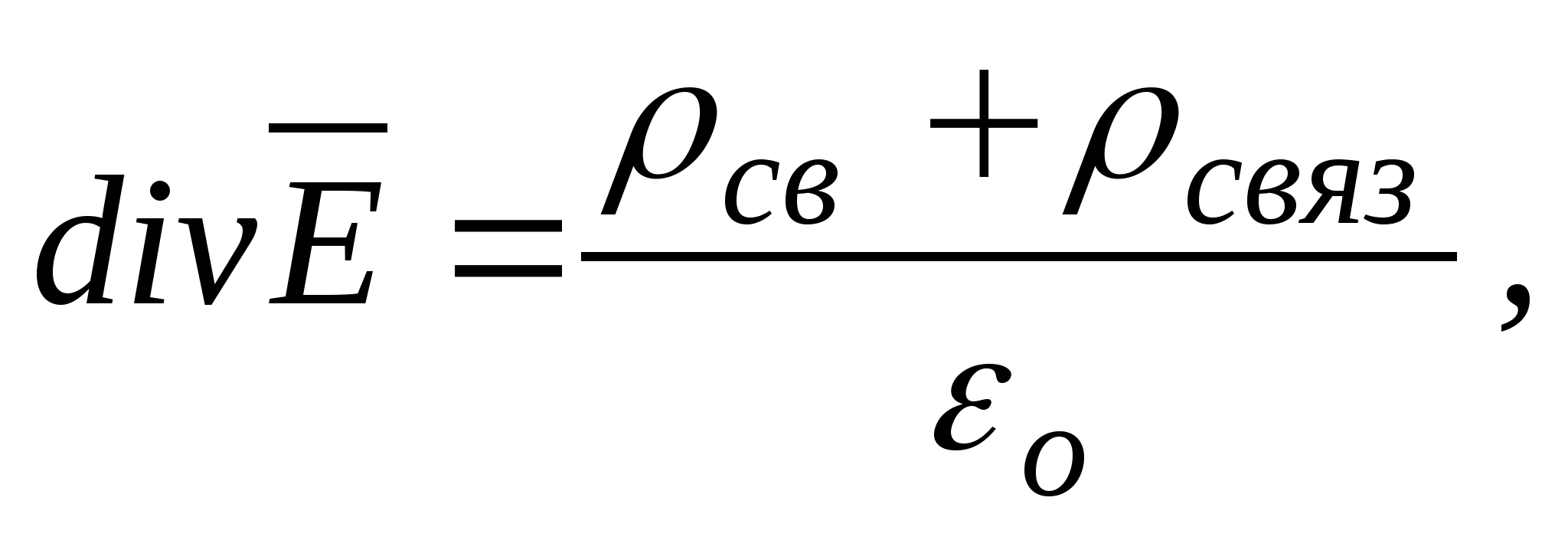 где ρ
где ρ
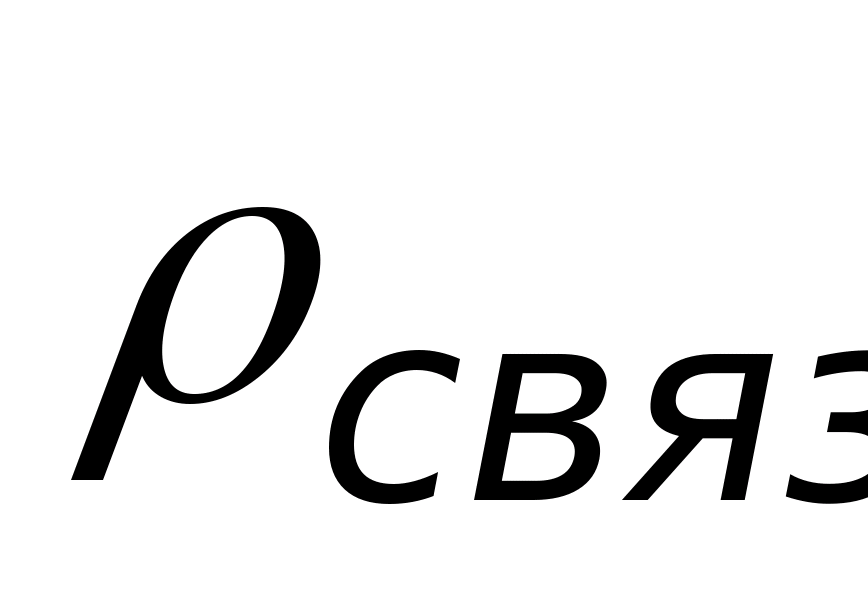
связ
-
объёмная плотность связанных зарядов.
Опуская вывод выражения
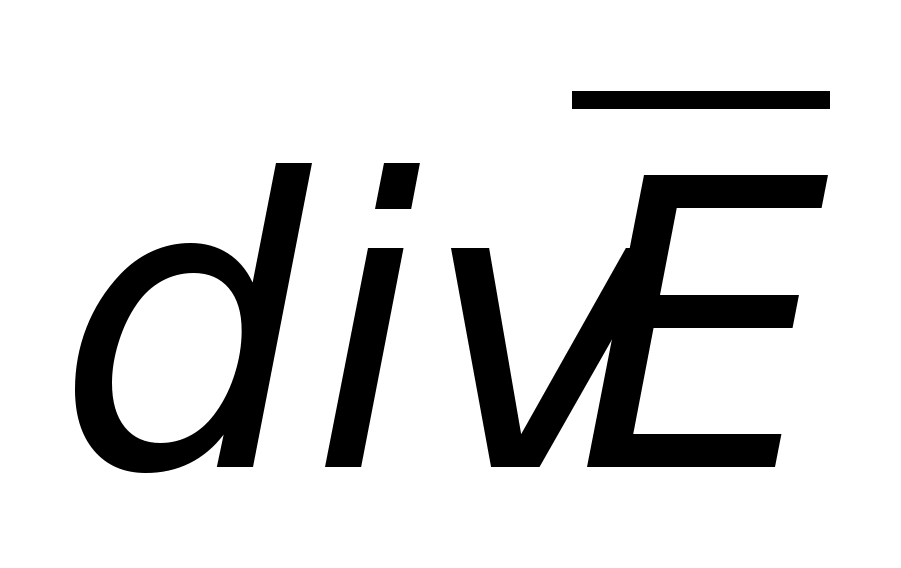 ,
запишем его в прямоугольной системе
координат
,
запишем его в прямоугольной системе
координат
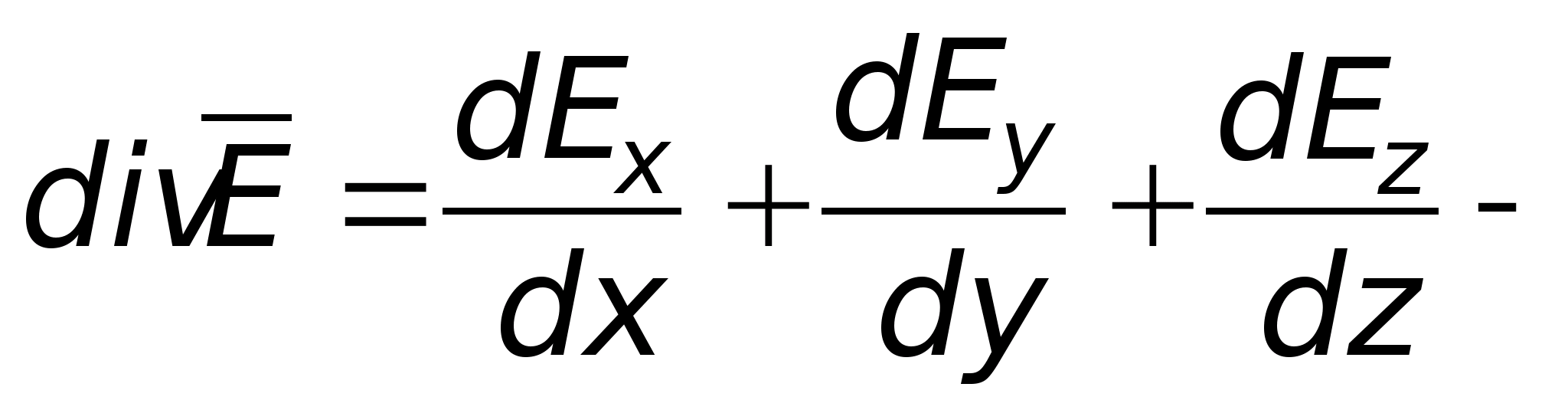 она
представляет собой сумму частных
производных проекций вектора Е
по трём координатным осям. Покажем, что
скалярное произведение оператора набла
и вектора Е
означает взятие дивергенции от последнего:
она
представляет собой сумму частных
производных проекций вектора Е
по трём координатным осям. Покажем, что
скалярное произведение оператора набла
и вектора Е
означает взятие дивергенции от последнего:
В связи с этим теорему Гаусса в
дифференциальной форме часто записывают
так
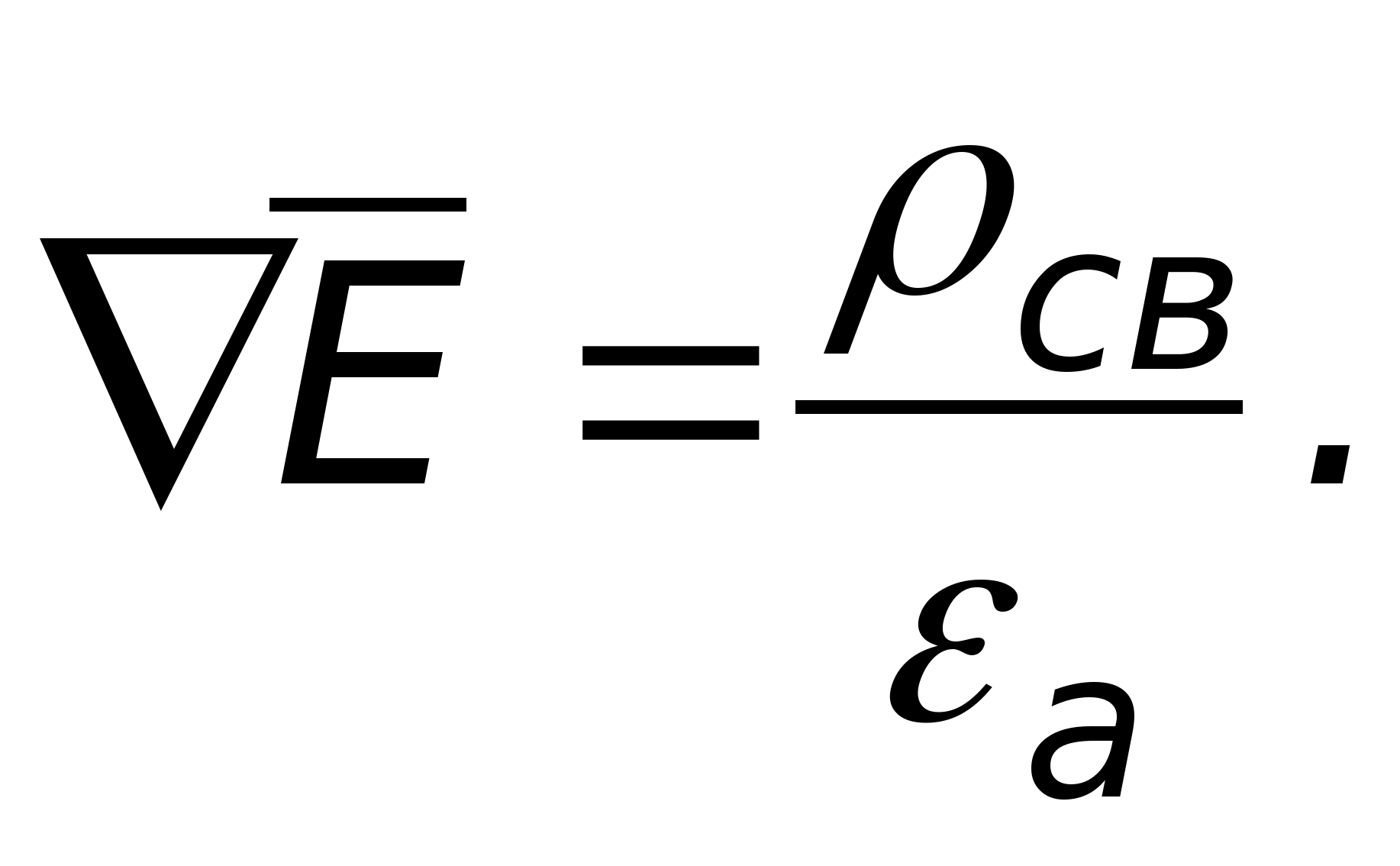
Уравнения Пуассона и Лапласа
Уравнения Пуассона и Лапласа
вытекают из теоремы Гаусса в дифформе
и тоже относятся к числу основных
уравнений электростатики.
Действительно, известно,
что
.
В тоже время
Подставляя первое выражение во второе,
получаем
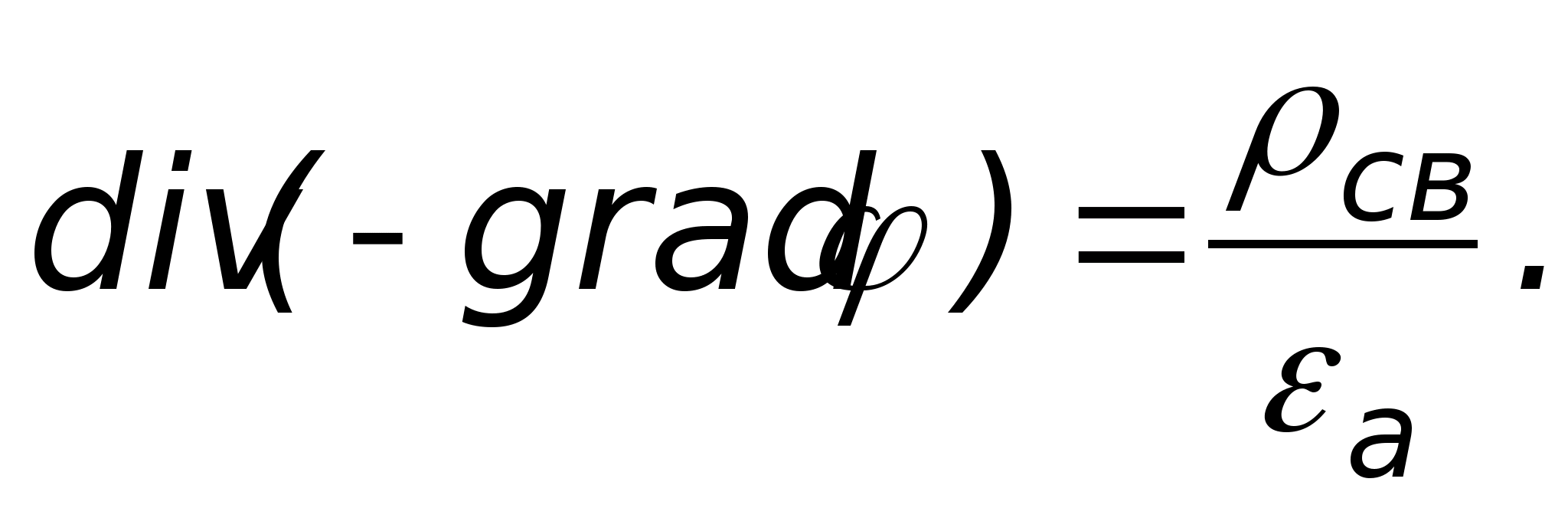 или
или
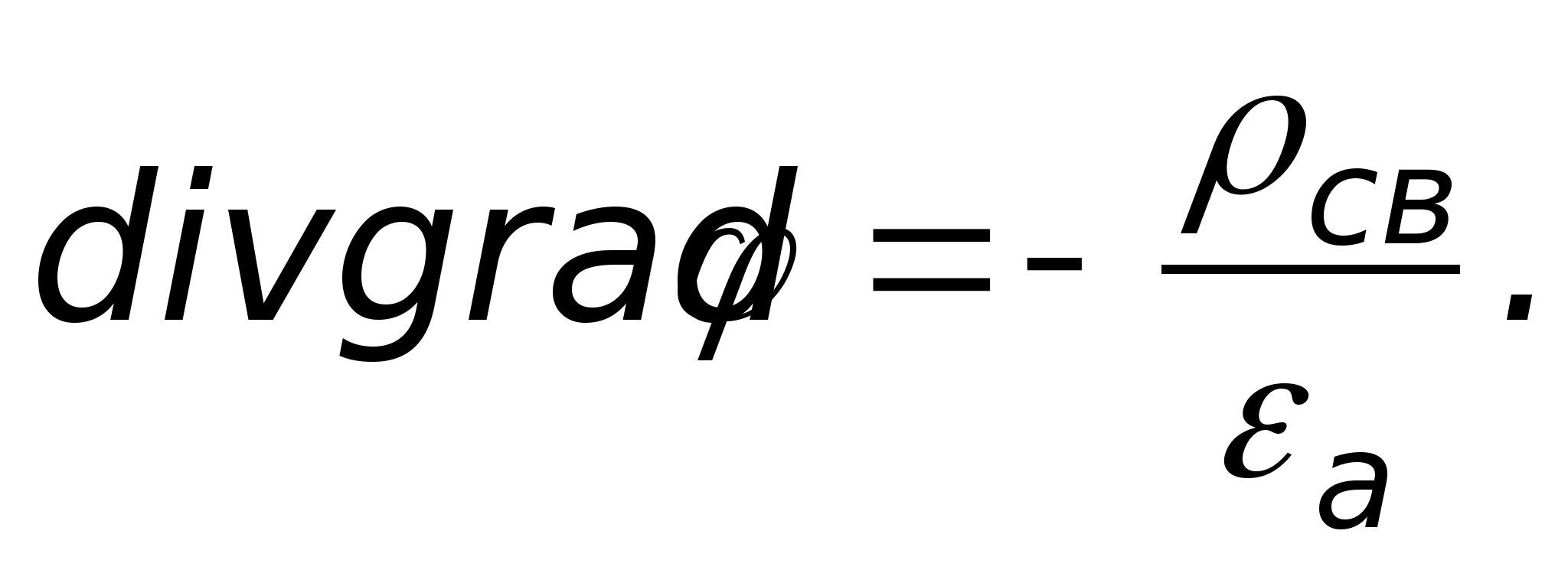 Вместо дивергенции и градиента можно
использовать оператор набла, тогда
получим
Вместо дивергенции и градиента можно
использовать оператор набла, тогда
получим
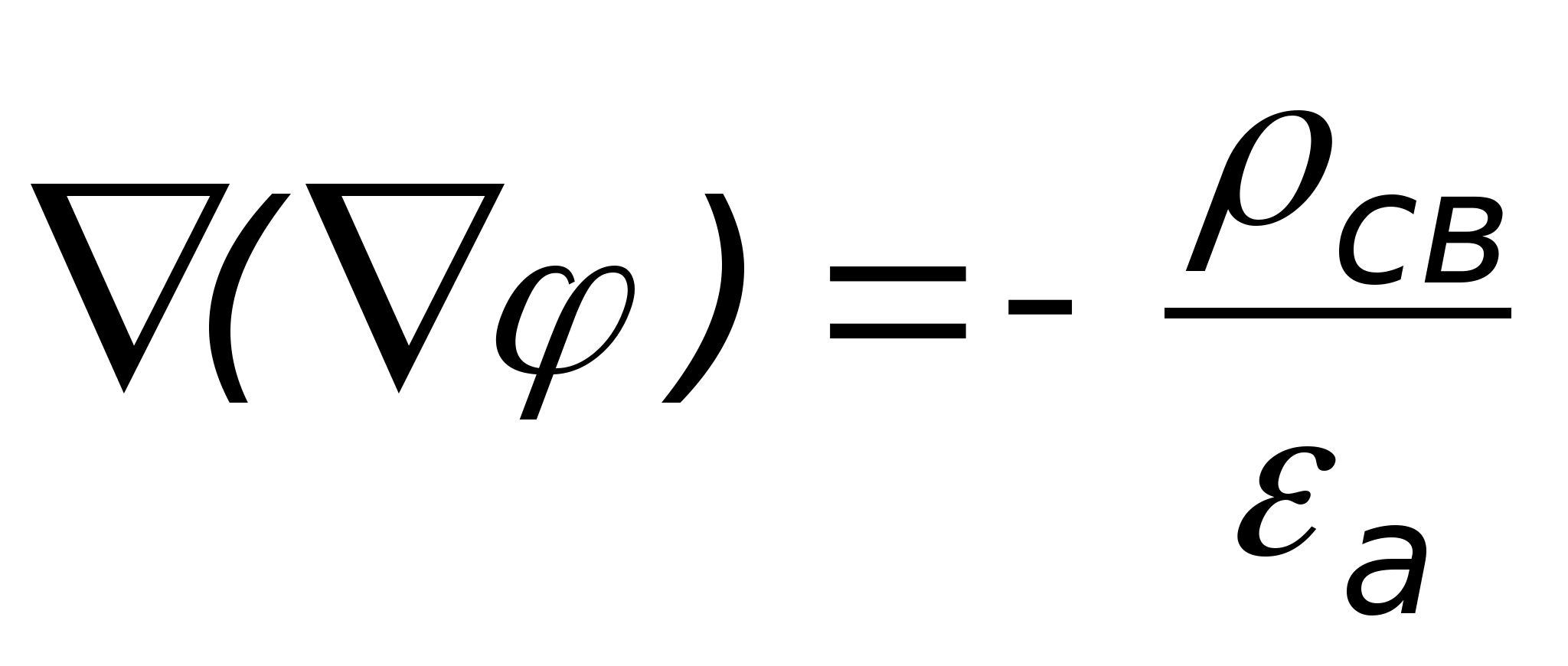 .
.
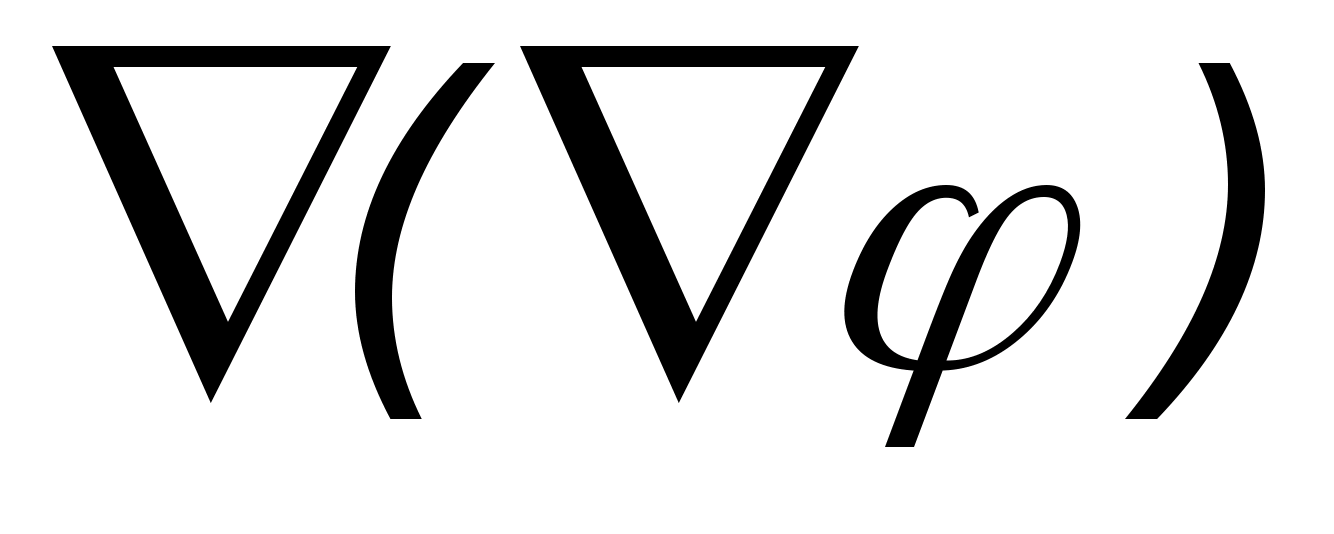 называется лапласианом и обозначается
так
называется лапласианом и обозначается
так
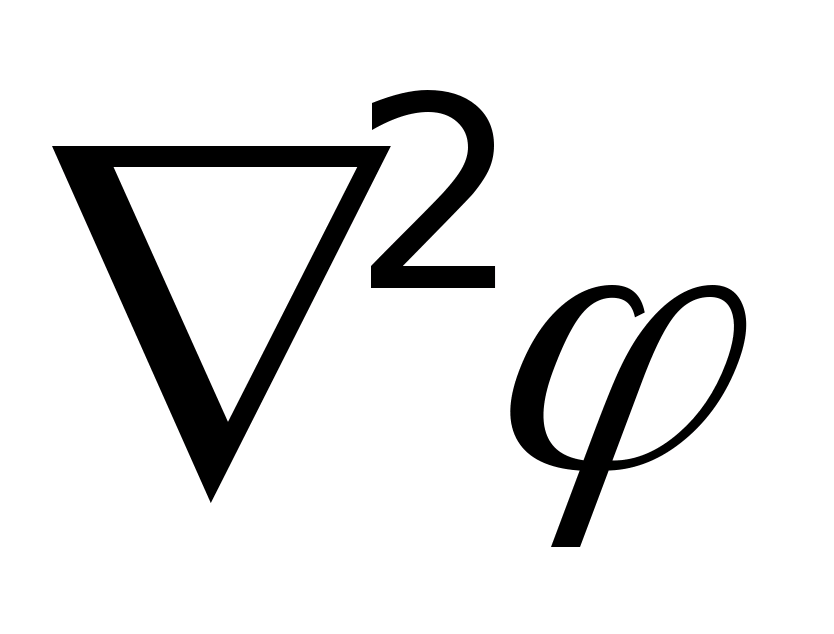 .
Тогда
.
Тогда
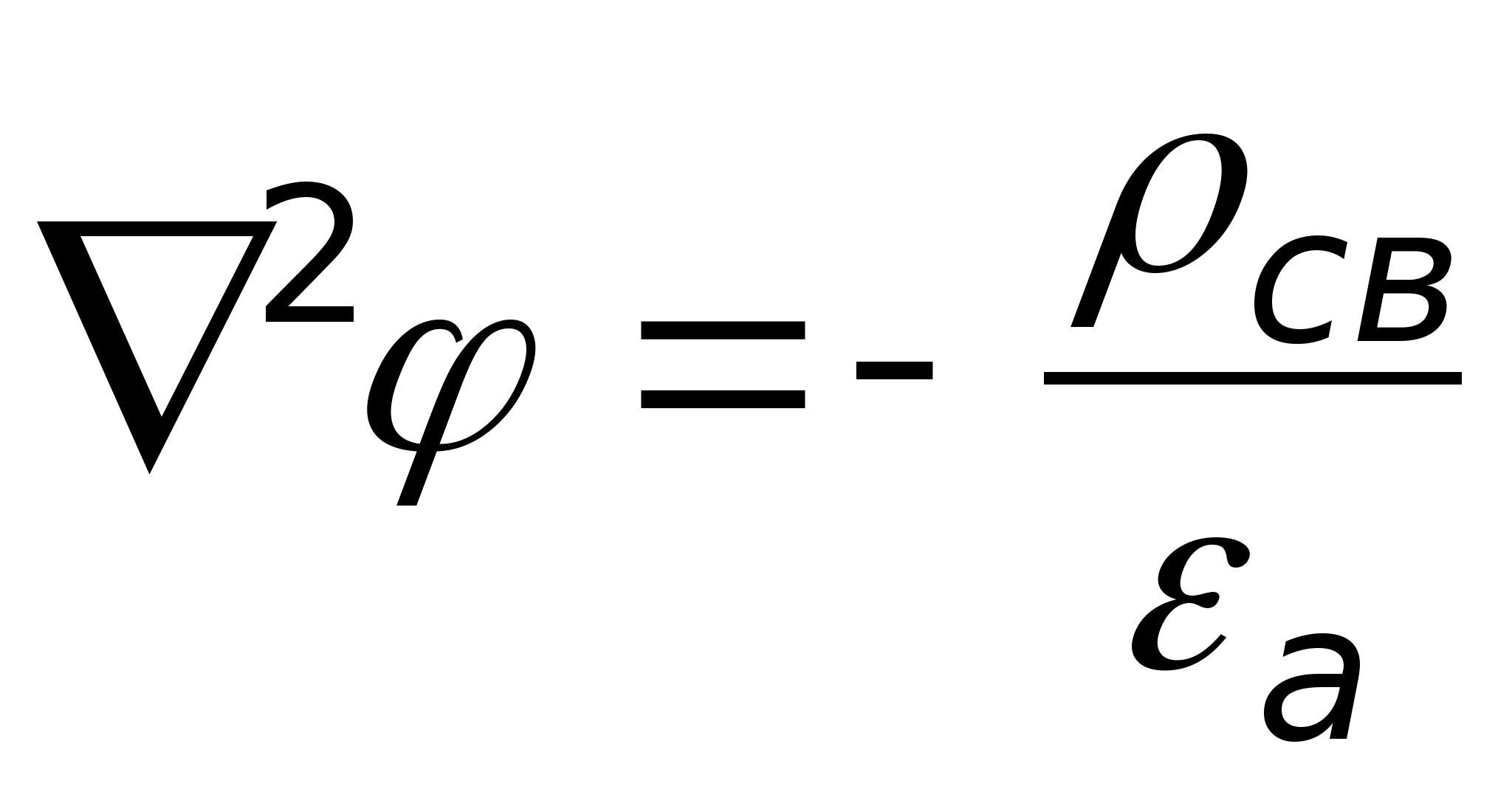 .
Это и есть уравнение Пуассона. Раскроем
лапласиан потенциала
в прямоугольной системе координат:
поскольку произведение одноименных
ортов даёт единицу, а разноименных –
ноль.
.
Это и есть уравнение Пуассона. Раскроем
лапласиан потенциала
в прямоугольной системе координат:
поскольку произведение одноименных
ортов даёт единицу, а разноименных –
ноль.
Частный вид уравнения Пуассона
при ρ
св
=0
называется уравнением Лапласа. Оно
выглядит так
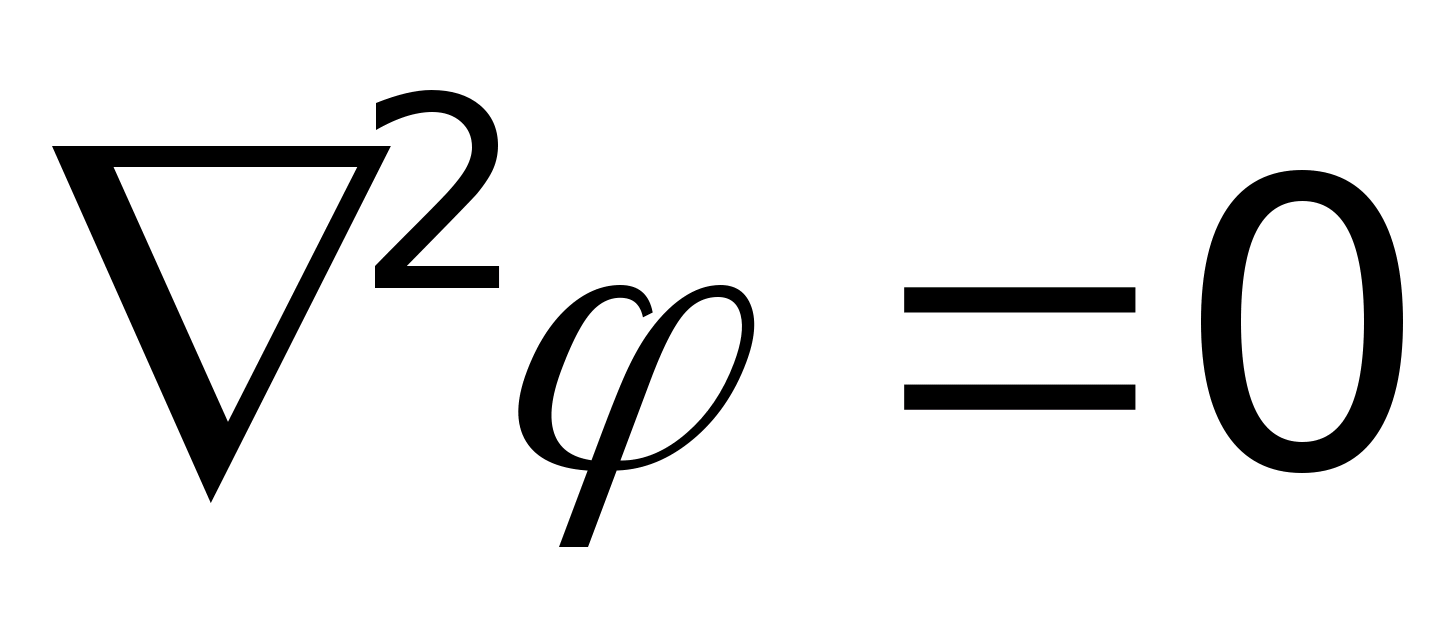 или в прямоугольной системе координат
или в прямоугольной системе координат
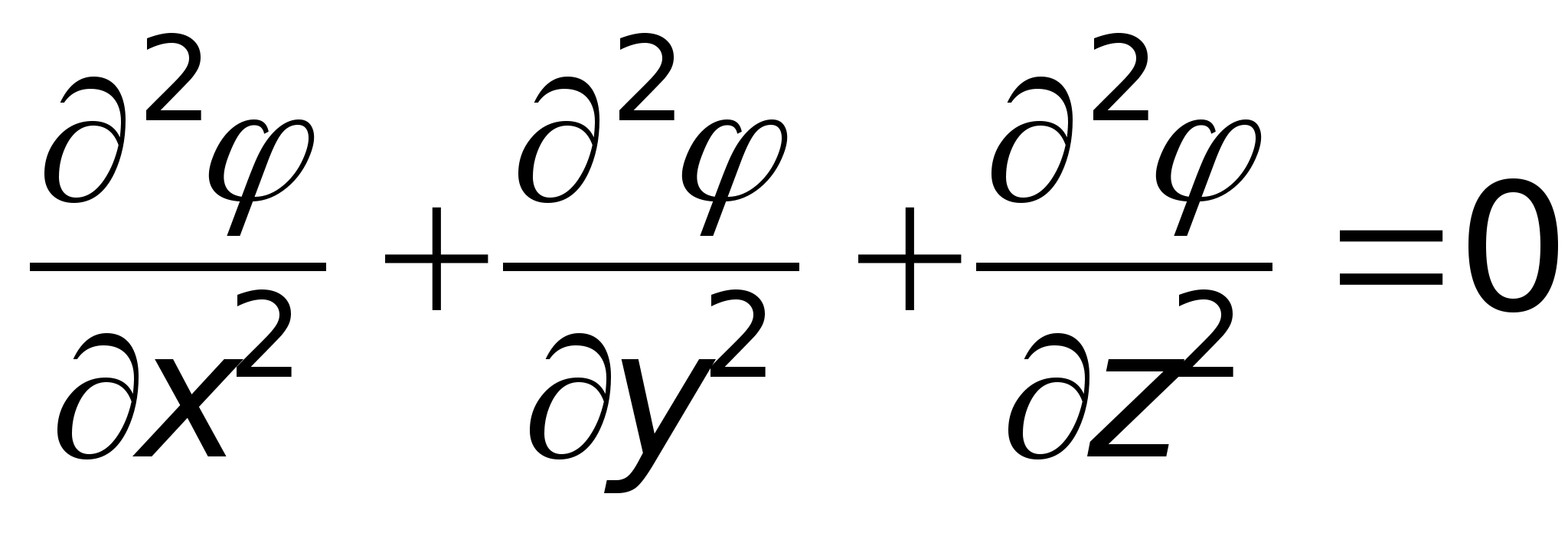 .
Уравнение Лапласа описывает области
электростатического поля, не занятые
свободным зарядом.
.
Уравнение Лапласа описывает области
электростатического поля, не занятые
свободным зарядом.
В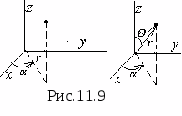 электростатике встречаются задачи,
которые значительно легче решаются не
в прямоугольной, а в цилиндрической или
сферической системе координат (рис.11.9).
Выражение лапласиана потенциала
в цилиндрической системе координат
имеет вид:
электростатике встречаются задачи,
которые значительно легче решаются не
в прямоугольной, а в цилиндрической или
сферической системе координат (рис.11.9).
Выражение лапласиана потенциала
в цилиндрической системе координат
имеет вид:
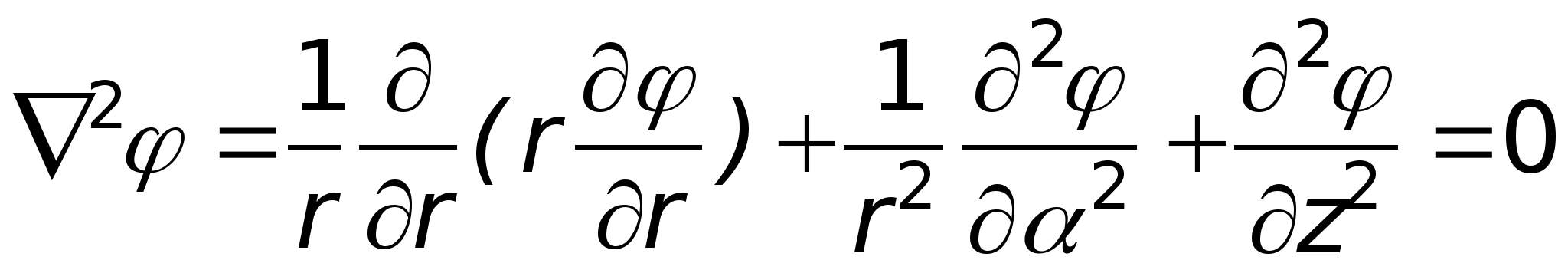 ,
а в сферической
.
,
а в сферической
.
Решение уравнений Пуассона и Лапласа в математическом отношении является весьма сложной задачей, но зато их решение позволяет определить закон изменения потенциала по известному распределению заряда. При решении этих уравнений появляются постоянные интегрирования, которые определяются исходя из граничных условий.
Граничные условия в электростатическом поле
П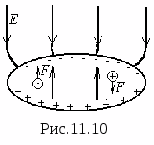 од
граничными условиями понимают условия,
которым удовлетворяет поле на границе
раздела двух различных сред. Прежде чем
перейти к обсуждению граничных условий,
рассмотрим поведение проводящего тела
в электростатическом поле. Проводящим
называется тело, в составе которого
имеются свободные заряды. Пусть некоторое
проводящее тело помещено в электростатическое
поле (рис.11.10). Тогда на каждый свободный
заряд со стороны поля начнет действовать
сила, под действием которой положительные
свободные заряды будут перемещаться в
сторону низкого потенциала, а отрицательные
– сторону высокого.
Перемещение зарядов
возможно только в пределах проводящего
тела, поэтому они скапливаются на его
поверхности (положительные – со стороны
низкого потенциала, а отрицательные –
со стороны высокого). Это
явление получило название электростатической
индукции, а скопившиеся на поверхности
проводника заряды называются
индуктированными.
Хотя сумма положительных
индуктированных зарядов в точности
равна сумме отрицательных и в целом
тело электрически нейтрально (если оно
не было предварительно заряжено), но
индуктированные заряды создают своё
поле, что приводит к изменению
результирующего поля внутри тела и
вблизи его и в его окрестности.
од
граничными условиями понимают условия,
которым удовлетворяет поле на границе
раздела двух различных сред. Прежде чем
перейти к обсуждению граничных условий,
рассмотрим поведение проводящего тела
в электростатическом поле. Проводящим
называется тело, в составе которого
имеются свободные заряды. Пусть некоторое
проводящее тело помещено в электростатическое
поле (рис.11.10). Тогда на каждый свободный
заряд со стороны поля начнет действовать
сила, под действием которой положительные
свободные заряды будут перемещаться в
сторону низкого потенциала, а отрицательные
– сторону высокого.
Перемещение зарядов
возможно только в пределах проводящего
тела, поэтому они скапливаются на его
поверхности (положительные – со стороны
низкого потенциала, а отрицательные –
со стороны высокого). Это
явление получило название электростатической
индукции, а скопившиеся на поверхности
проводника заряды называются
индуктированными.
Хотя сумма положительных
индуктированных зарядов в точности
равна сумме отрицательных и в целом
тело электрически нейтрально (если оно
не было предварительно заряжено), но
индуктированные заряды создают своё
поле, что приводит к изменению
результирующего поля внутри тела и
вблизи его и в его окрестности.
Все точки проводящего тела имеют
один и тот же потенциал, так как если
допустить, что между двумя точками
имеется разность потенциалов, то под
действием этой разности протечет ток
и потенциалы уравновесятся. Так как все
точки проводящего тела имеют один и тот
же потенциал, то напряженность
электростатического поля внутри его
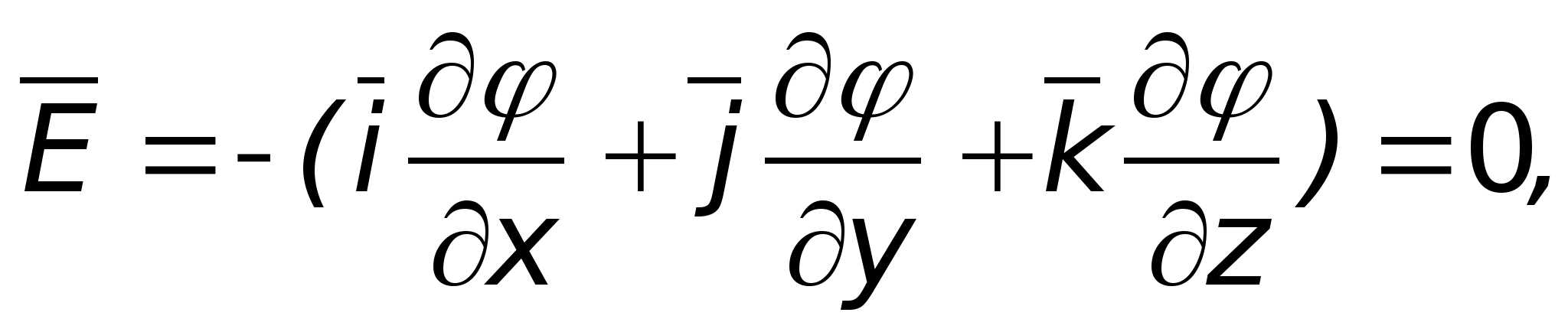 т.е. поле внутри проводящего тела
отсутствует. С физической точки зрения
это объясняется тем, что внешнее поле
полностью компенсируется полем
индуктированных зарядов (см. рис.11.10).
Индуктированных зарядов наводится
именно столько и располагаются они
именно так, чтобы внутри проводящего
тела поля полностью компенсировались.
Таким образом, объём, занятый проводящим
телом является эквипотенциальным.
Описанное свойство проводящих тел
используется на практике для экранирования
аппаратуры от воздействия внешних
электростатических полей.
т.е. поле внутри проводящего тела
отсутствует. С физической точки зрения
это объясняется тем, что внешнее поле
полностью компенсируется полем
индуктированных зарядов (см. рис.11.10).
Индуктированных зарядов наводится
именно столько и располагаются они
именно так, чтобы внутри проводящего
тела поля полностью компенсировались.
Таким образом, объём, занятый проводящим
телом является эквипотенциальным.
Описанное свойство проводящих тел
используется на практике для экранирования
аппаратуры от воздействия внешних
электростатических полей.
Условия на границе раздела диэлектрика и проводящего тела. На такой границе выполняются два условия: для всех точек диэлектрика, непосредственно примыкающих к поверхности проводника равна нулю тангенциальная составляющая напряженности поля (E t =0), а вектор электрического смещения численно равен поверхностной плотности индуктированного заряда (D=σ ).
Д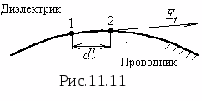 ля
доказательства первого условия возьмём
две точки (1 и 2) на границе раздела
диэлектрик-проводник (рис.11.11).
Тангенциальная составляющая вектора
Е
будет
направлена по линии, соединяющей эти
точки и определится так
ля
доказательства первого условия возьмём
две точки (1 и 2) на границе раздела
диэлектрик-проводник (рис.11.11).
Тангенциальная составляющая вектора
Е
будет
направлена по линии, соединяющей эти
точки и определится так
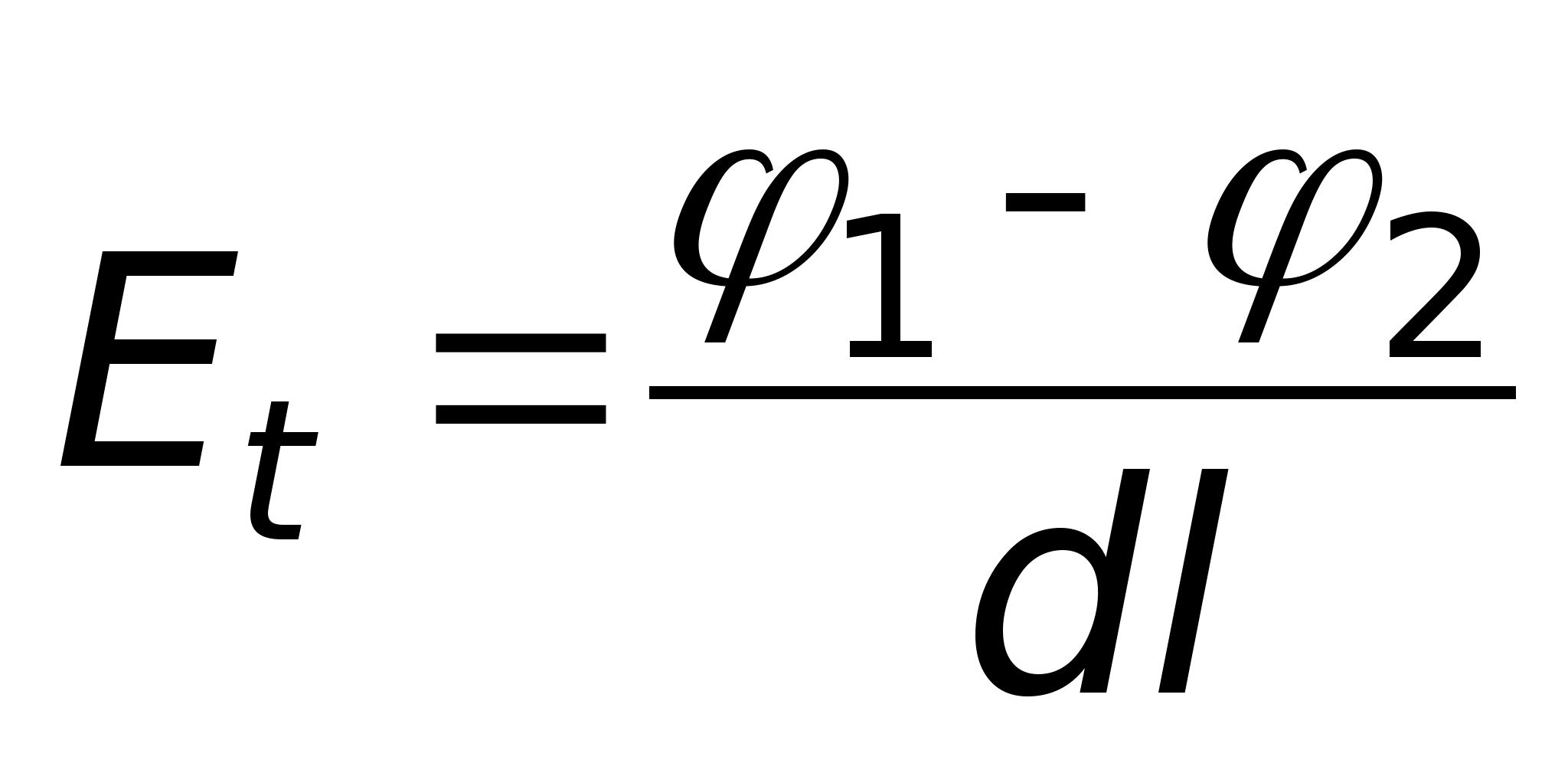 ,
но
,
но
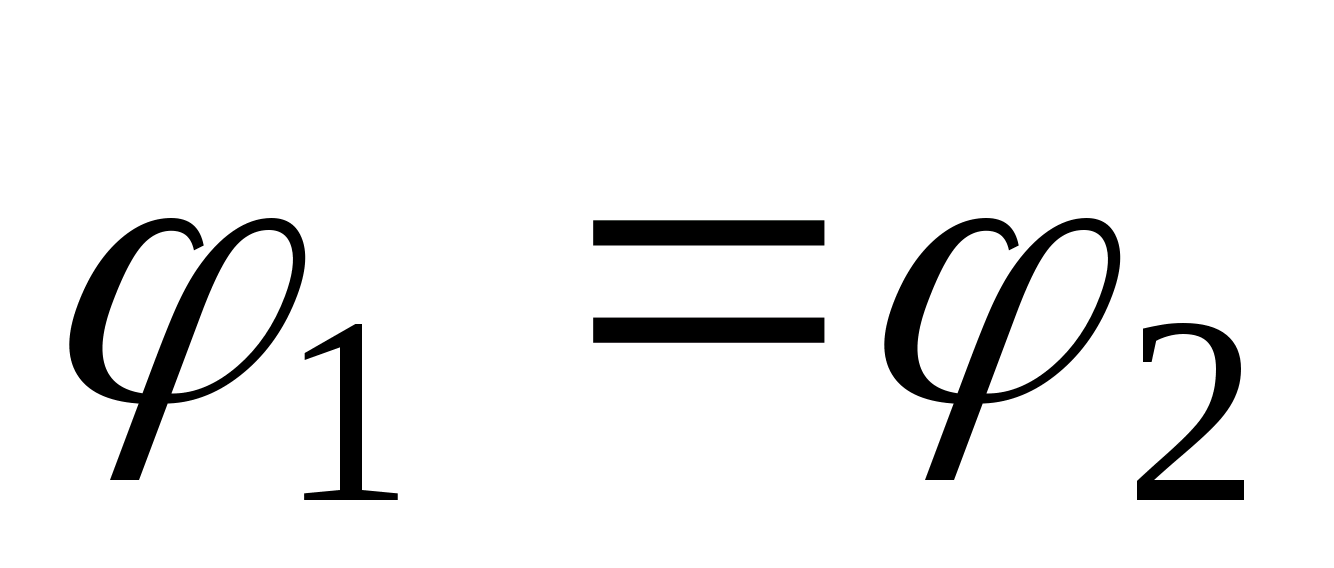 ,
т.к. точки 1 и 2 принадлежат и проводнику,
а
,
т.к. точки 1 и 2 принадлежат и проводнику,
а
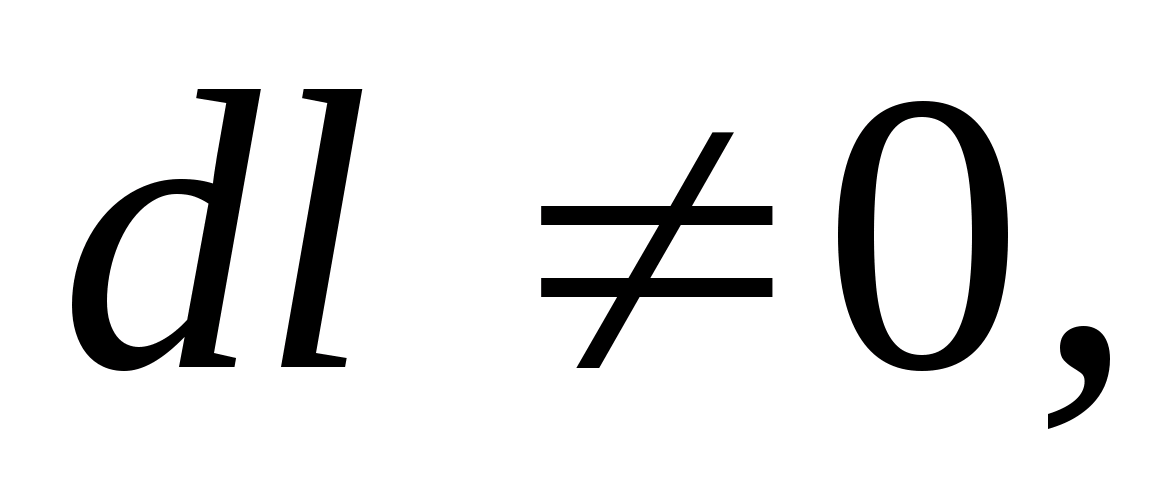 поэтому
E
t
=0,
что и требовалось доказать.
Таким образом, силовые линии
электростатического поля подходят к
поверхности проводника под прямым углом
(E
t
=0).
поэтому
E
t
=0,
что и требовалось доказать.
Таким образом, силовые линии
электростатического поля подходят к
поверхности проводника под прямым углом
(E
t
=0).
Д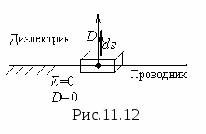 ля
доказательства второго условия возьмем
произвольную точку на границе и окружим
её бесконечно малым плоским объёмом в
виде параллелепипеда (рис.11.12) и применим
к нему теорему Гаусса в интегральной
форме
ля
доказательства второго условия возьмем
произвольную точку на границе и окружим
её бесконечно малым плоским объёмом в
виде параллелепипеда (рис.11.12) и применим
к нему теорему Гаусса в интегральной
форме
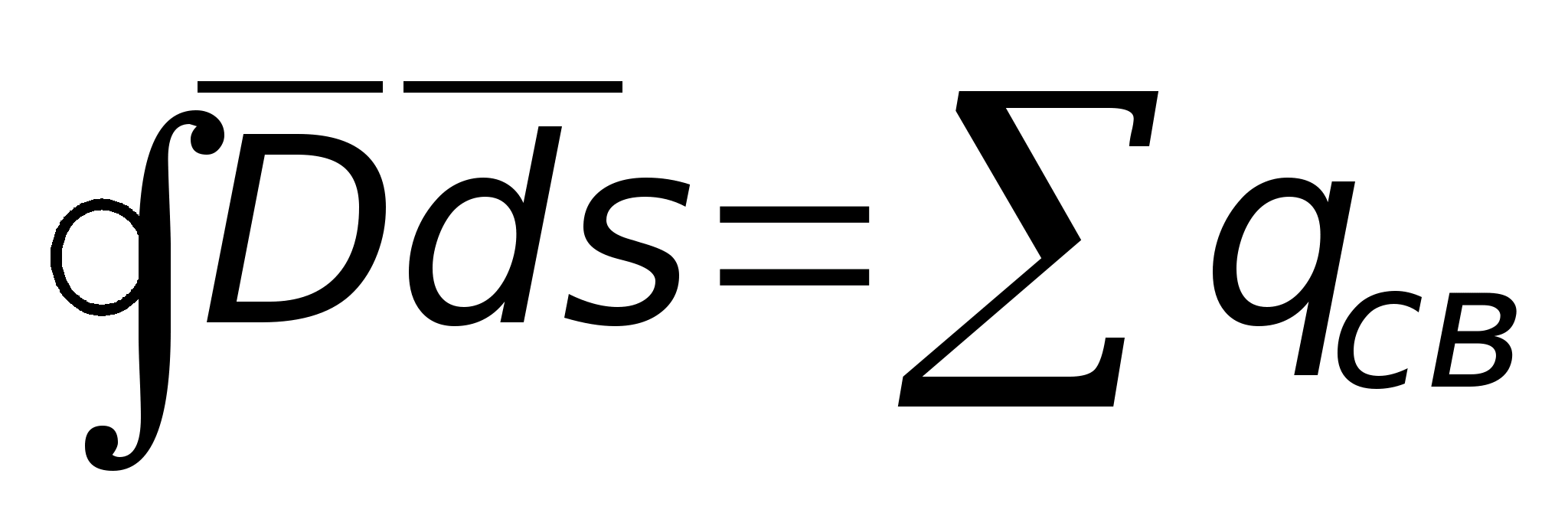 .
Поскольку нижняя грань находится в
проводящей среде, то через неё поток
вектора D
равен нулю, также как и через боковые
грани (эти грани бесконечно малы, кроме
того вектор D
скользит вдоль них). Поток
вектора D
через верхнюю грань равен
.
Поскольку нижняя грань находится в
проводящей среде, то через неё поток
вектора D
равен нулю, также как и через боковые
грани (эти грани бесконечно малы, кроме
того вектор D
скользит вдоль них). Поток
вектора D
через верхнюю грань равен
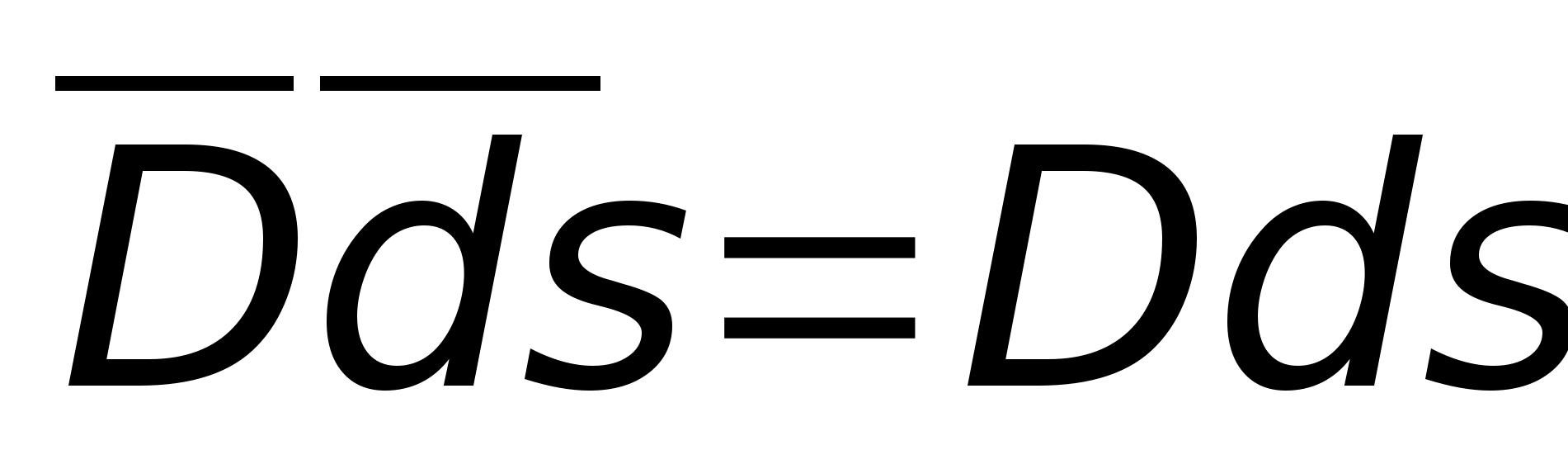 ,
т.к. векторы D
и
ds
совпадают по направлению.
Внутри поверхности
интегрирования находятся только
индуктированные заряды и их количество
равно
,
т.к. векторы D
и
ds
совпадают по направлению.
Внутри поверхности
интегрирования находятся только
индуктированные заряды и их количество
равно
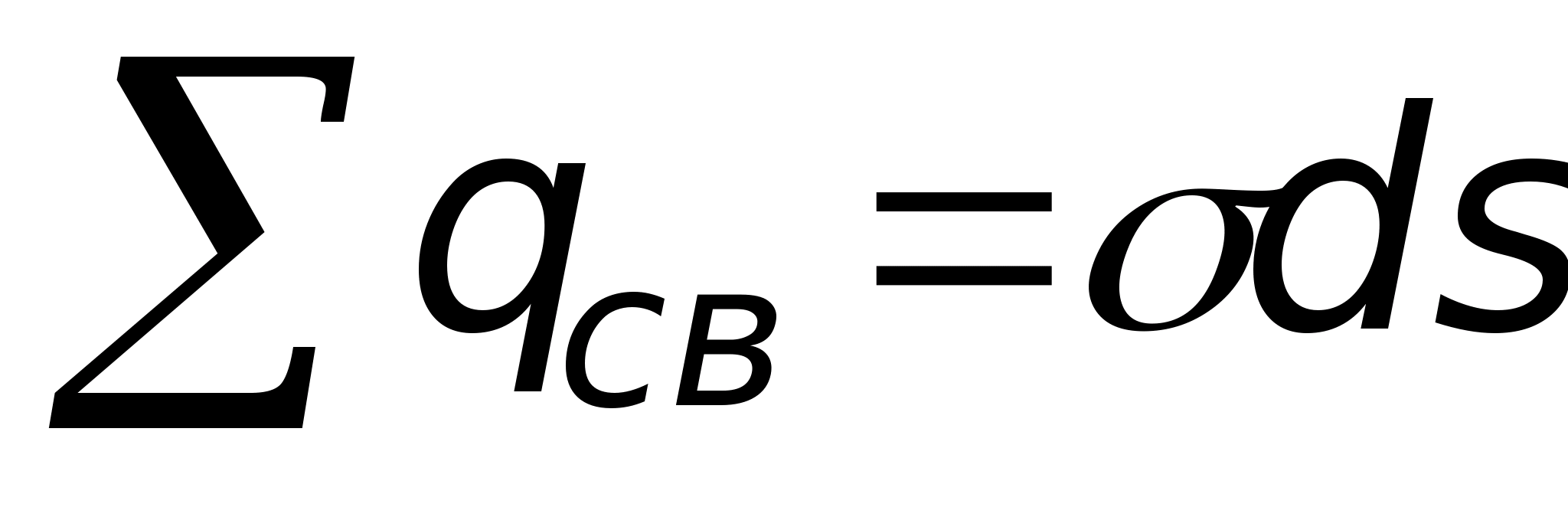 ,
где
,
где
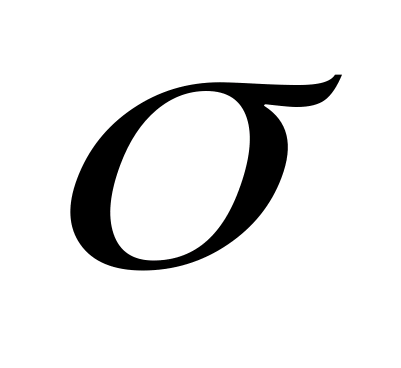 - поверхностная плотность индуктированного
заряда. Тогда
- поверхностная плотность индуктированного
заряда. Тогда
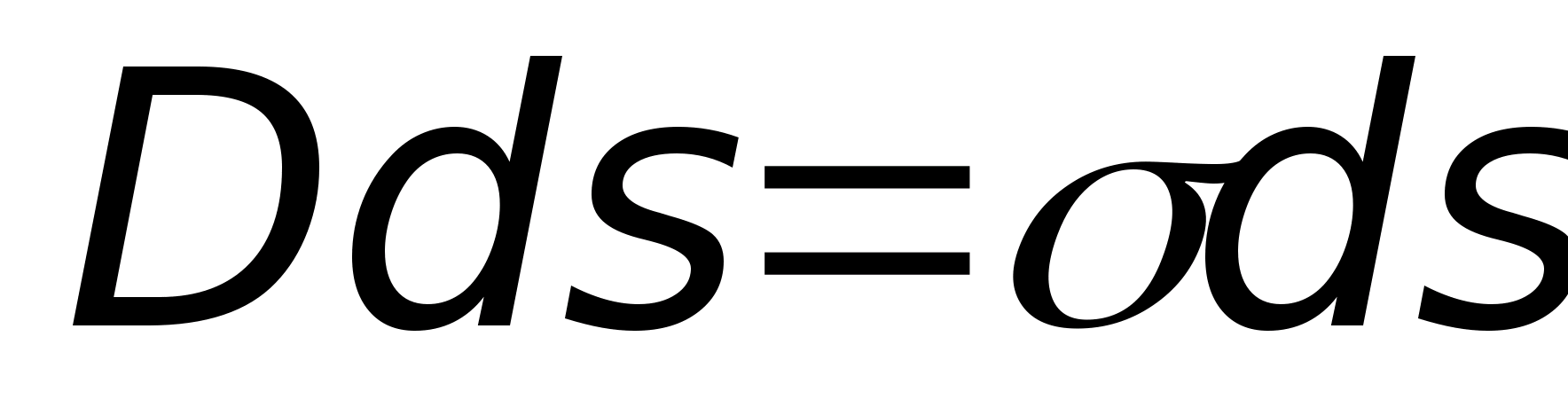 или
или
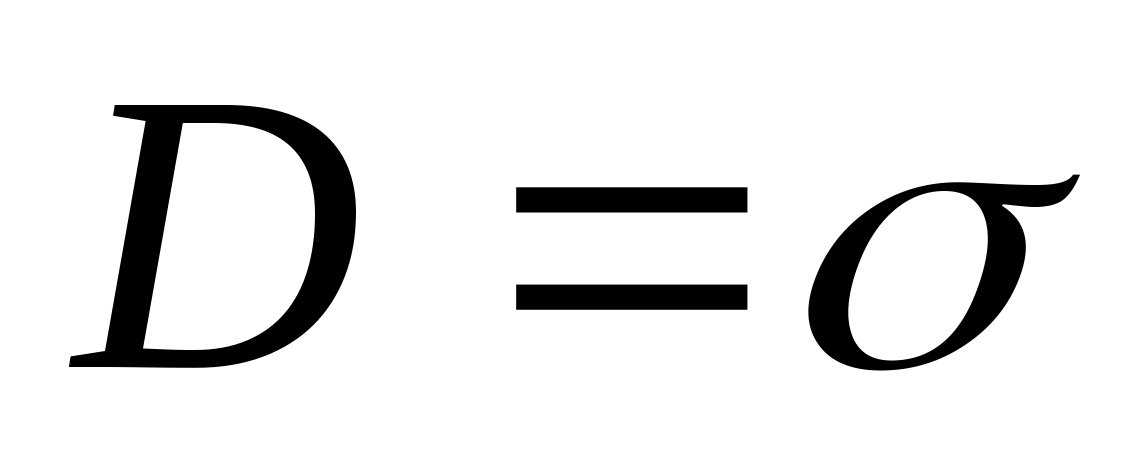 .
.
У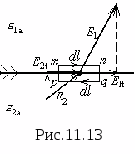 словия
на границе раздела двух различных
диэлектриков.
На такой
границе выполняются два условия: для
всех точек, являющихся общими для двух
различных диэлектриков, равны по величине
тангенциальные составляющие вектора
Е
(Е
1 t =Е
2 t)и
нормальные
составляющие вектора D
(D
1n
=D
2n
).
словия
на границе раздела двух различных
диэлектриков.
На такой
границе выполняются два условия: для
всех точек, являющихся общими для двух
различных диэлектриков, равны по величине
тангенциальные составляющие вектора
Е
(Е
1 t =Е
2 t)и
нормальные
составляющие вектора D
(D
1n
=D
2n
).
Покажем справедливость первого
условия для чего возьмём произвольную
точку на границе раздела двух различных
диэлектриков и окружим её бесконечно
малым (длина
- dl
mnpq
(рис.11.13).
Составим
выражение циркуляции вектора
E
вдоль этого контура.
Сторона mn
находится
в верхней среде и, если контур обходить
по часовой стрелке, то составляющая
циркуляции вдоль этой стороны
.
Аналогично для стороны pq
,
находящейся во второй среде
.
В последнем выражении минус стоит
потому, что тангенциальная составляющая
Е
2t
и вектор dl
направлены в противоположные
стороны. Составляющими циркуляции
вектора Е
вдоль сторон pm
и nq
можно пренебречь в силу
малости этих сторон. Для потенциального
поля, которым является электростатическое,
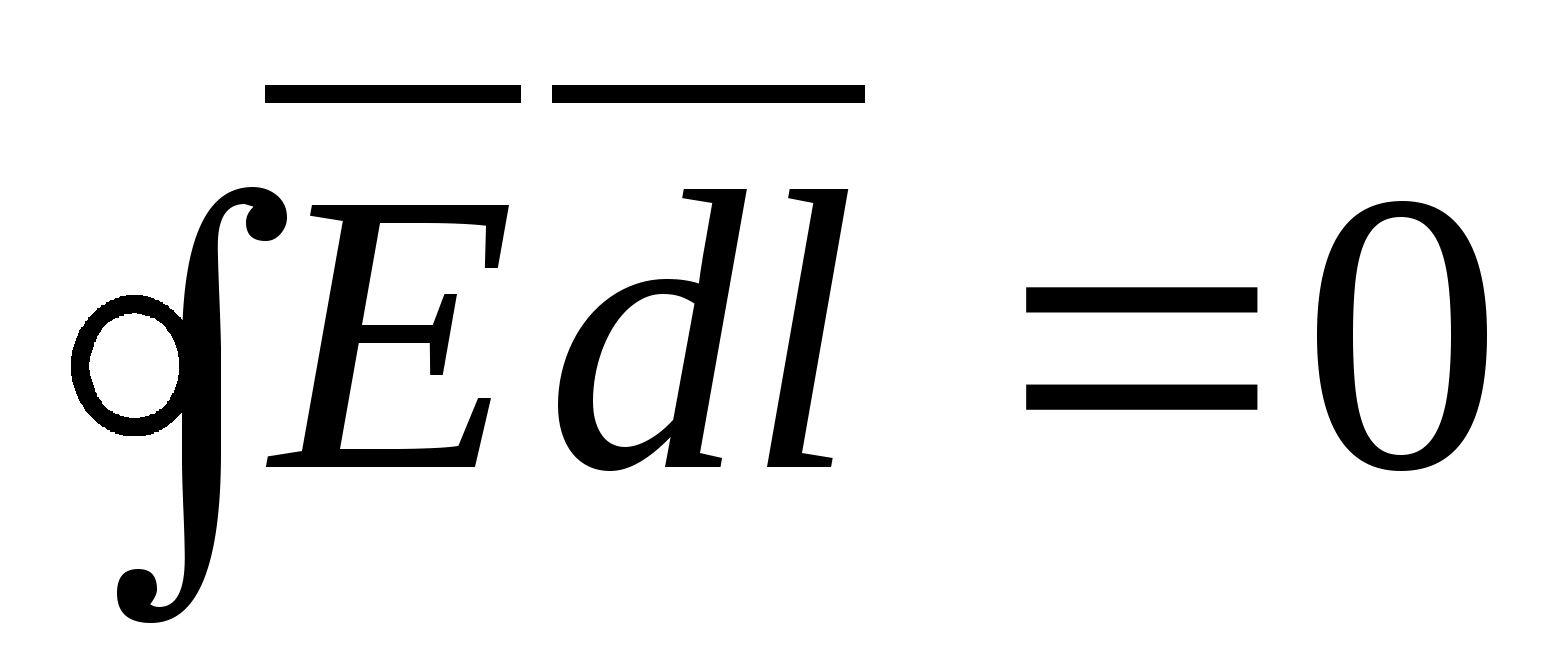 .
Тогда
.
Тогда
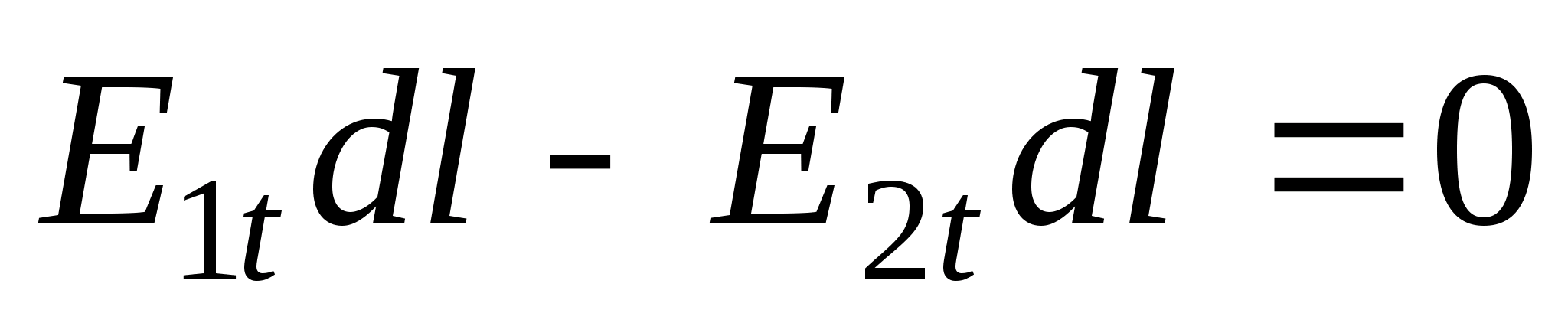 или
или
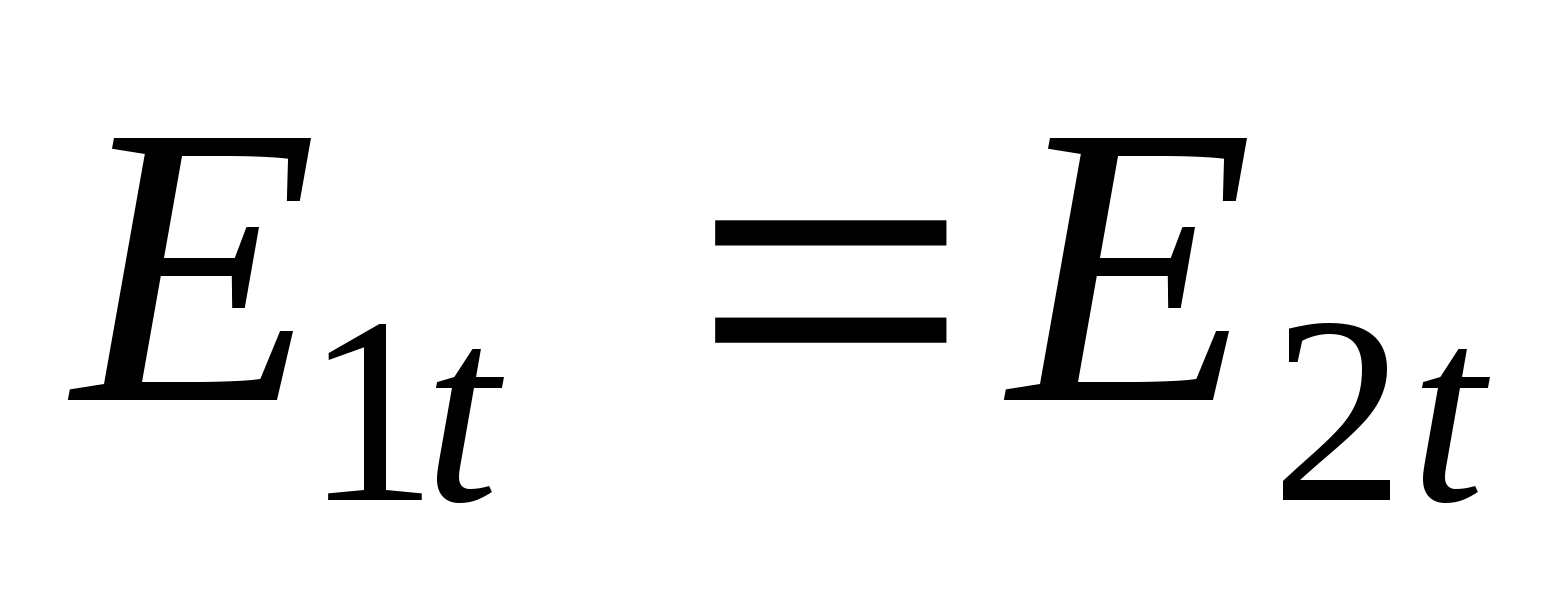 ,
что и требовалось доказать.
,
что и требовалось доказать.
Д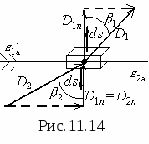 ля
доказательства второго условия возьмем
произвольную точку на границе и окружим
её бесконечно малым плоским объёмом в
виде параллелепипеда (рис.11.14) и применим
к нему теорему Гаусса в интегральной
форме
.
Через боковые грани потоком вектора D
можно
пренебречь из-за малости этих граней,
а через верхнюю и нижнюю – соответственно
и
.
Следовательно,
ля
доказательства второго условия возьмем
произвольную точку на границе и окружим
её бесконечно малым плоским объёмом в
виде параллелепипеда (рис.11.14) и применим
к нему теорему Гаусса в интегральной
форме
.
Через боковые грани потоком вектора D
можно
пренебречь из-за малости этих граней,
а через верхнюю и нижнюю – соответственно
и
.
Следовательно,
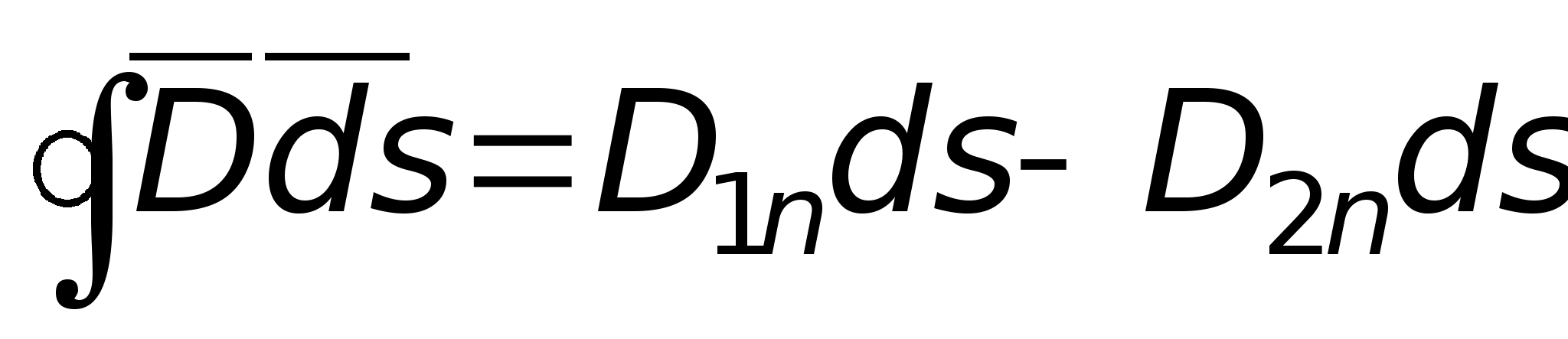 .
Внутри выделенного объёма нет свободных
зарядов, т.е.
.
Внутри выделенного объёма нет свободных
зарядов, т.е.
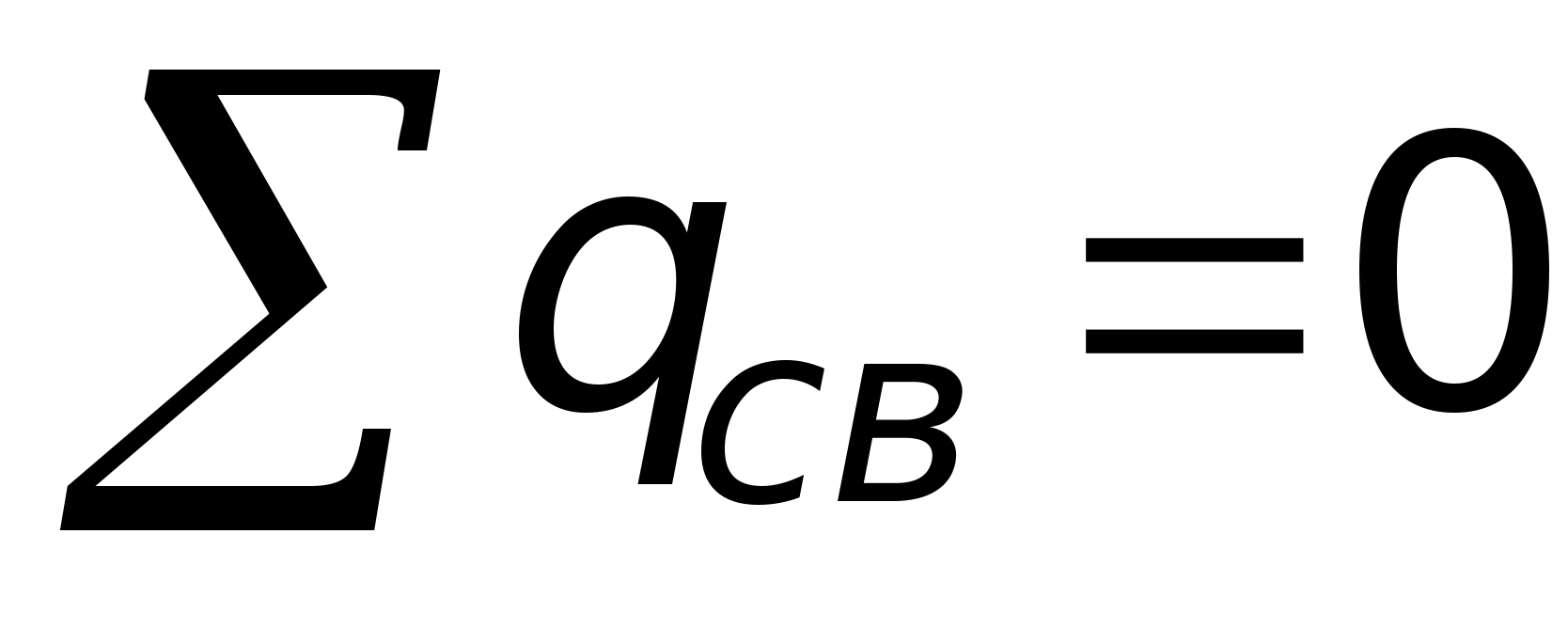 .
Тогда
.
Тогда
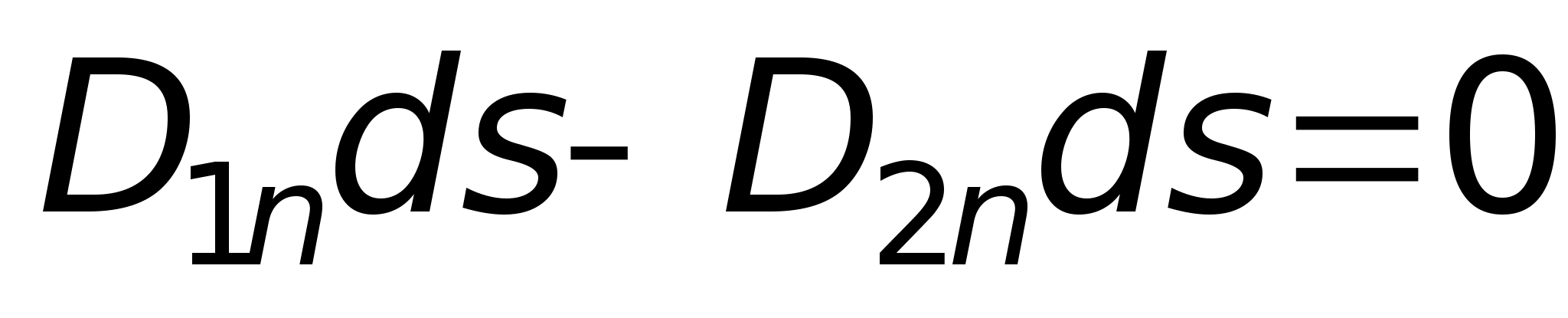 или
или
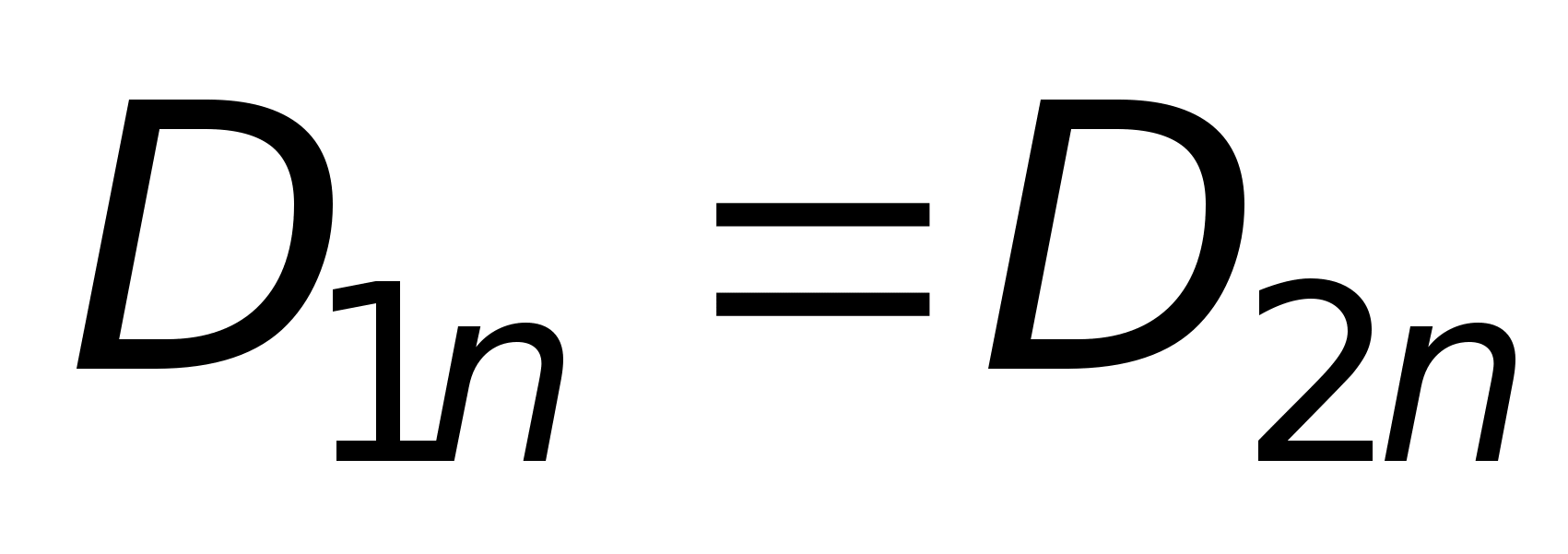 .
Если на границе раздела двух диэлектриков
присутствуют свободные заряды с
поверхностной плотностью σ (встречается
очень редко), то
.
Если на границе раздела двух диэлектриков
присутствуют свободные заряды с
поверхностной плотностью σ (встречается
очень редко), то
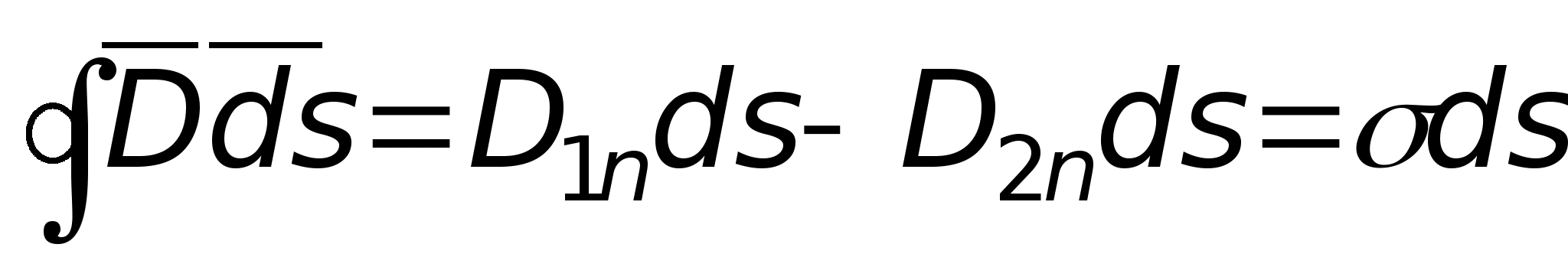 или
или
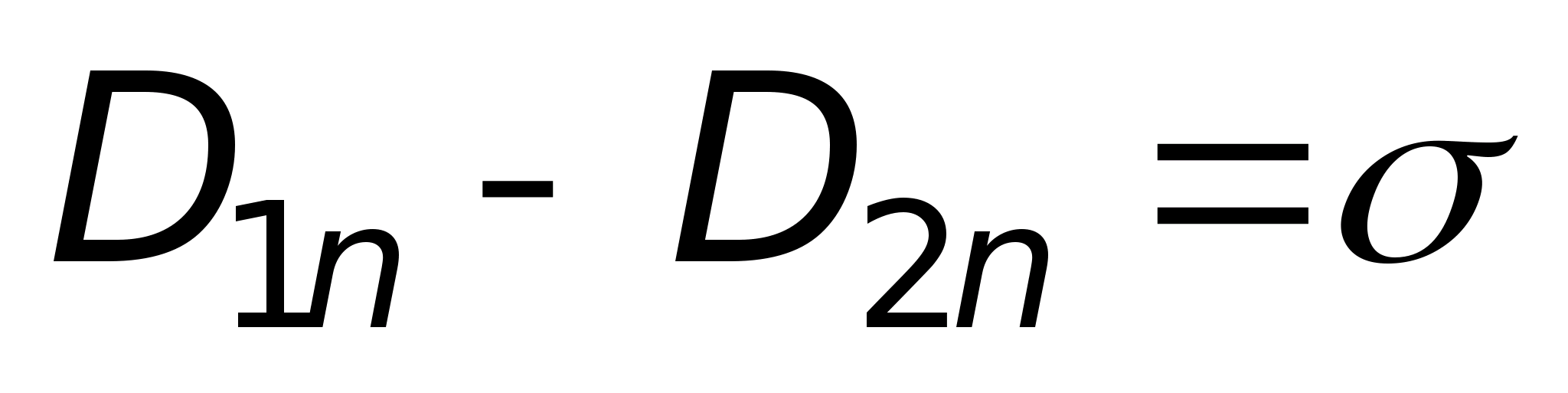 ,
т.е. при наличии на границе раздела
свободных зарядов нормальная составляющая
вектора D
претерпевает скачок на
величину поверхностной плотности
свободного заряда.
,
т.е. при наличии на границе раздела
свободных зарядов нормальная составляющая
вектора D
претерпевает скачок на
величину поверхностной плотности
свободного заряда.
Электростатическое поле заряженной оси
З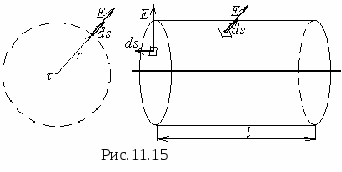 аряженной
осью называется очень тонкий, теоретически
бесконечно длинный проводник, несущий
на себе заряд. Весь заряд оси указать
невозможно (он равен бесконечности),
поэтому указывается линейный заряд
аряженной
осью называется очень тонкий, теоретически
бесконечно длинный проводник, несущий
на себе заряд. Весь заряд оси указать
невозможно (он равен бесконечности),
поэтому указывается линейный заряд
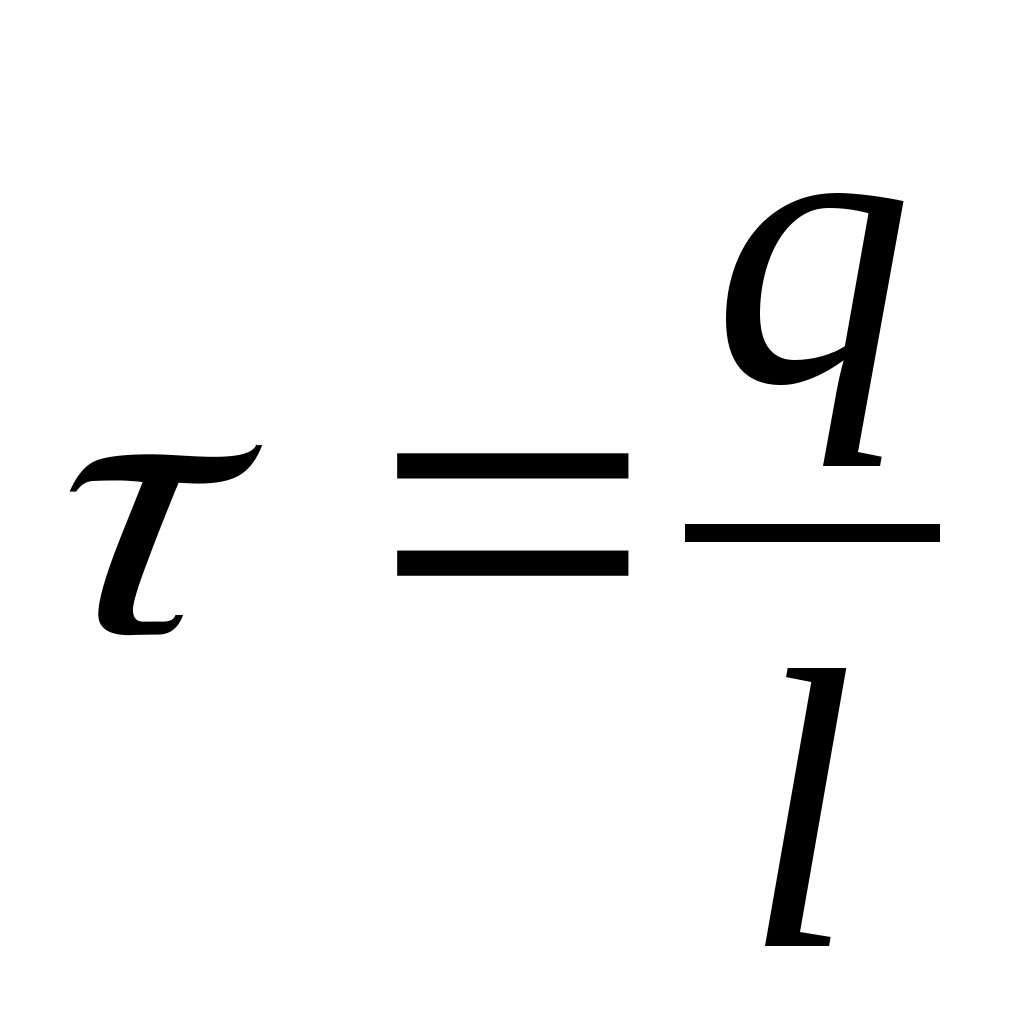 ,
т.е. заряд, приходящийся на единицу длины
оси. Пусть ось с положительным зарядом
τ
находится
в среде с проницаемостью ε
а
(рис.11.15). Используя
интегральную форму теоремы Гаусса,
произведем расчет напряженности поля
в произвольной точке, удаленной на
расстояние r
от оси. С этой целью
проведем через данную точку замкнутую
поверхность в виде цилиндра длиной l
.
Поток вектора Е
имеет место только через боковую
поверхность этого цилиндра,
поскольку в точках,
расположенных на его донышках векторы
Е
и ds
перпендикулярны и их
произведение равно нулю.
В точках же боковой
поверхности векторы Е
и ds
совпадают по направлению
и их произведение равно произведению
модулей, а модуль Е
одинаков во всех этих точках в силу
симметрии. С учетом сказанного имеем
Внутри поверхности интегрирования
заряд
,
т.е. заряд, приходящийся на единицу длины
оси. Пусть ось с положительным зарядом
τ
находится
в среде с проницаемостью ε
а
(рис.11.15). Используя
интегральную форму теоремы Гаусса,
произведем расчет напряженности поля
в произвольной точке, удаленной на
расстояние r
от оси. С этой целью
проведем через данную точку замкнутую
поверхность в виде цилиндра длиной l
.
Поток вектора Е
имеет место только через боковую
поверхность этого цилиндра,
поскольку в точках,
расположенных на его донышках векторы
Е
и ds
перпендикулярны и их
произведение равно нулю.
В точках же боковой
поверхности векторы Е
и ds
совпадают по направлению
и их произведение равно произведению
модулей, а модуль Е
одинаков во всех этих точках в силу
симметрии. С учетом сказанного имеем
Внутри поверхности интегрирования
заряд
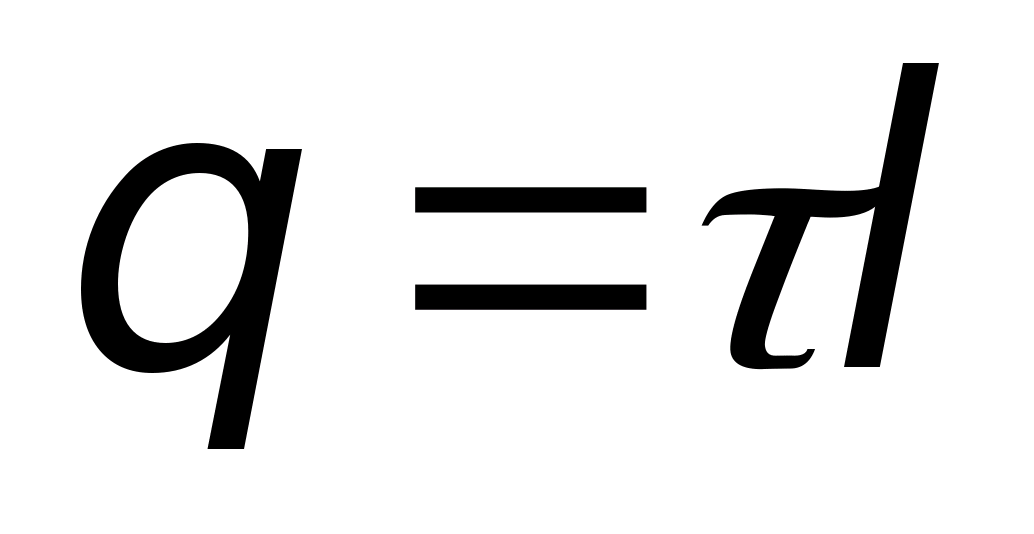 .
Поэтому
.
Поэтому
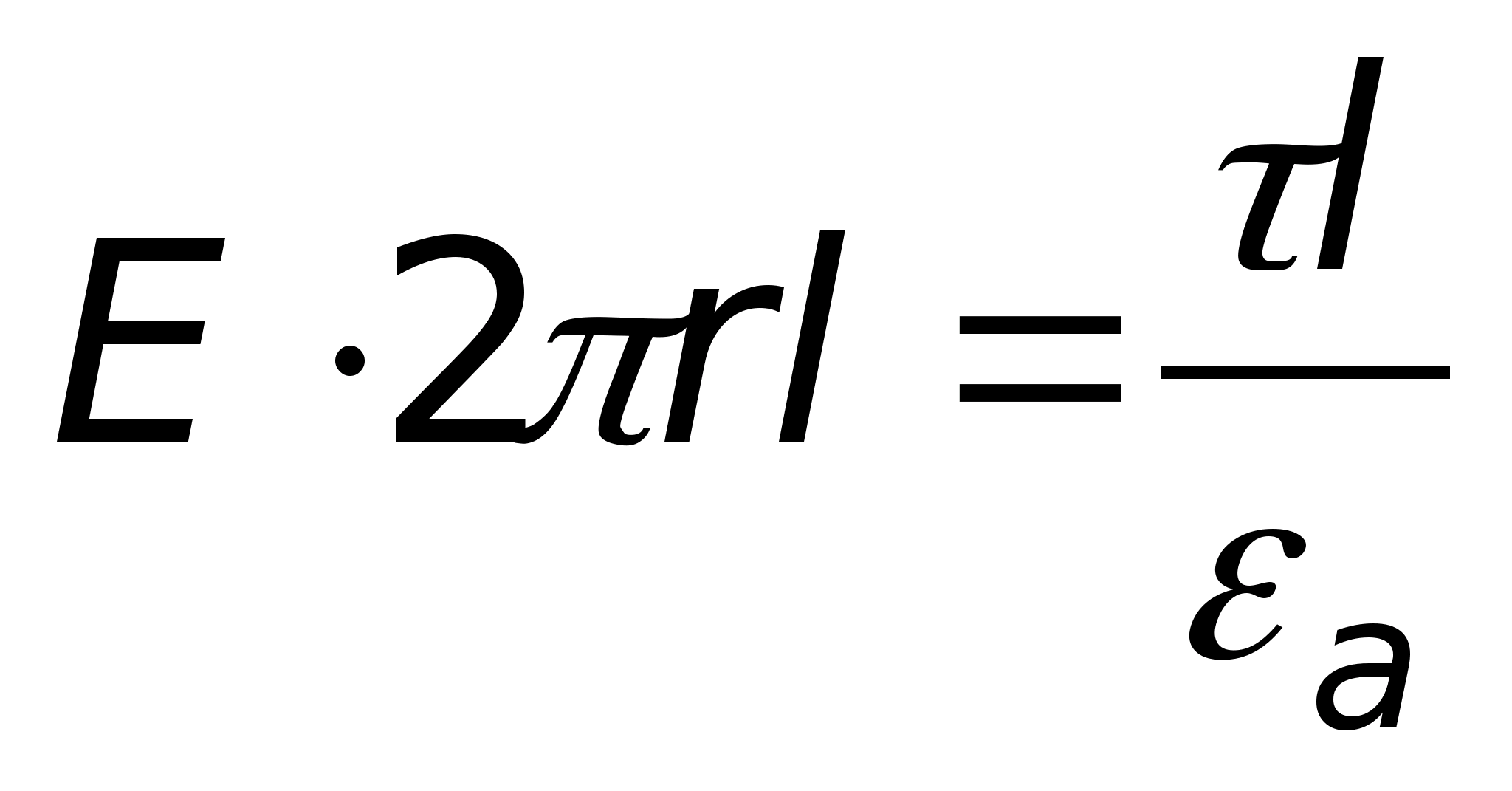 или
или
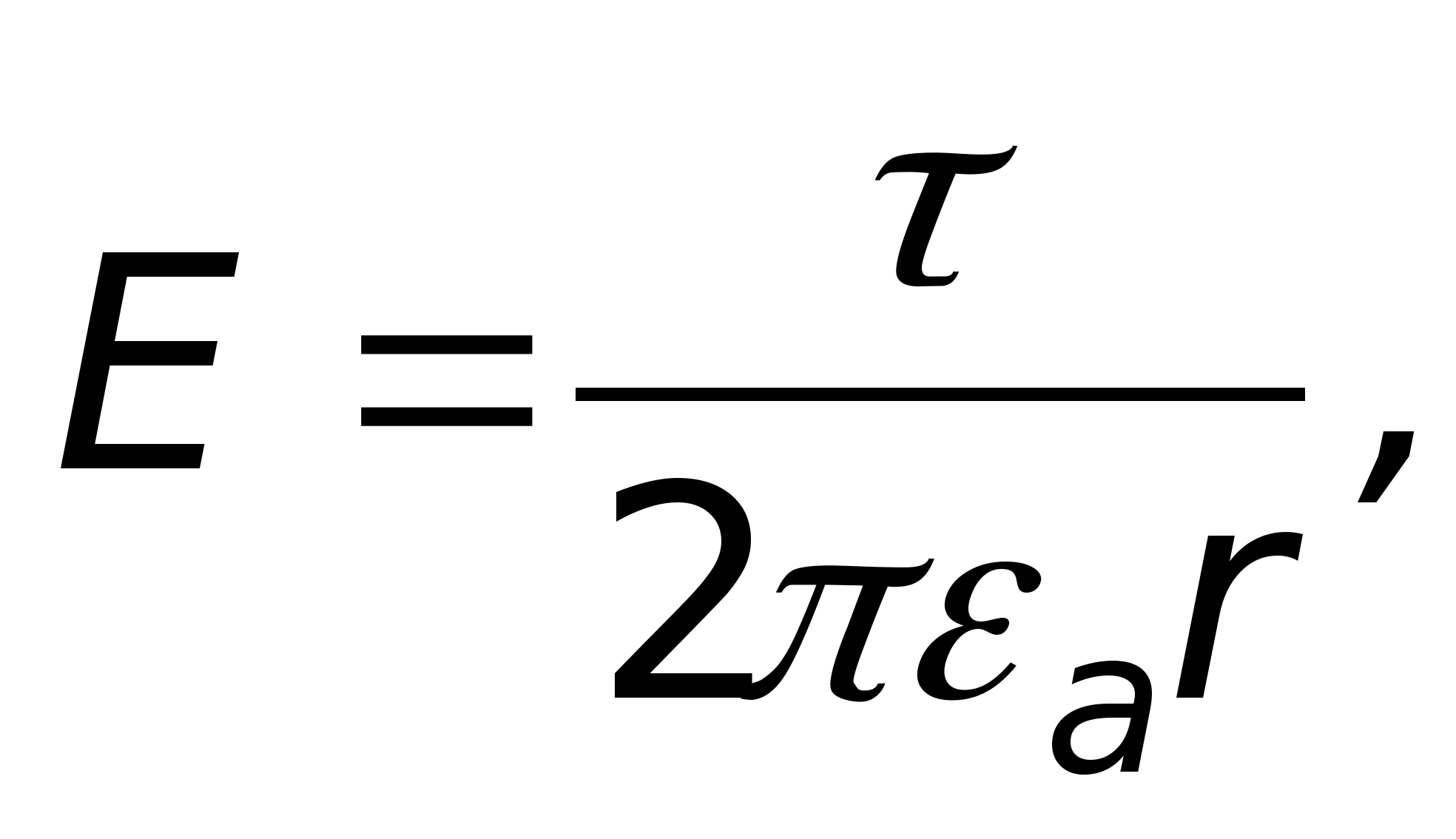 т.е. напряженность в данном поле изменяется
обратно пропорционально расстоянию от
оси.
т.е. напряженность в данном поле изменяется
обратно пропорционально расстоянию от
оси.
Потенциал Постоянная интегрирования А зависит от того, где расположить точку с нулевым потенциалом. Следовательно, в данном поле потенциал изменяется по логарифмическому закону.
Электростатическое поле двух заряженных осей
Н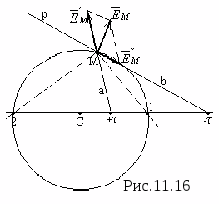 а
практике чаще всего две заряженные оси
несут на себе равные по величине и
противоположные по знаку заряды +E
ds l r
τ
и -τ
. Именно такой случай и рассмотрим
(рис.11.16). Возьмем в поле произвольную
точку М
, положение которой будем
характеризовать расстоянием а
до
положительной оси и расстоянием b
до отрицательной оси и в первую очередь
рассчитаем в ней напряженность поля,
используя метод наложения:
а
практике чаще всего две заряженные оси
несут на себе равные по величине и
противоположные по знаку заряды +E
ds l r
τ
и -τ
. Именно такой случай и рассмотрим
(рис.11.16). Возьмем в поле произвольную
точку М
, положение которой будем
характеризовать расстоянием а
до
положительной оси и расстоянием b
до отрицательной оси и в первую очередь
рассчитаем в ней напряженность поля,
используя метод наложения:
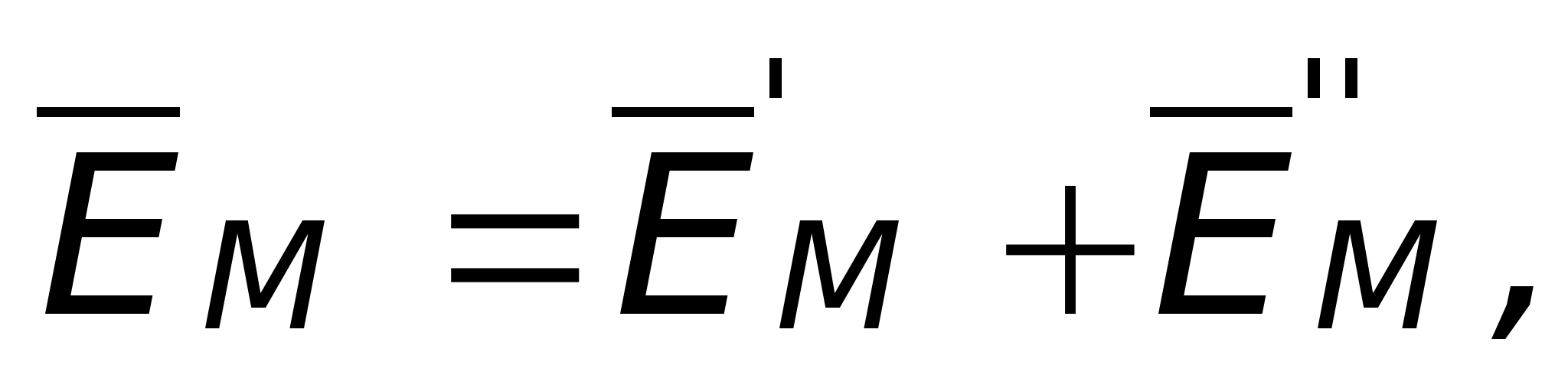 где
где
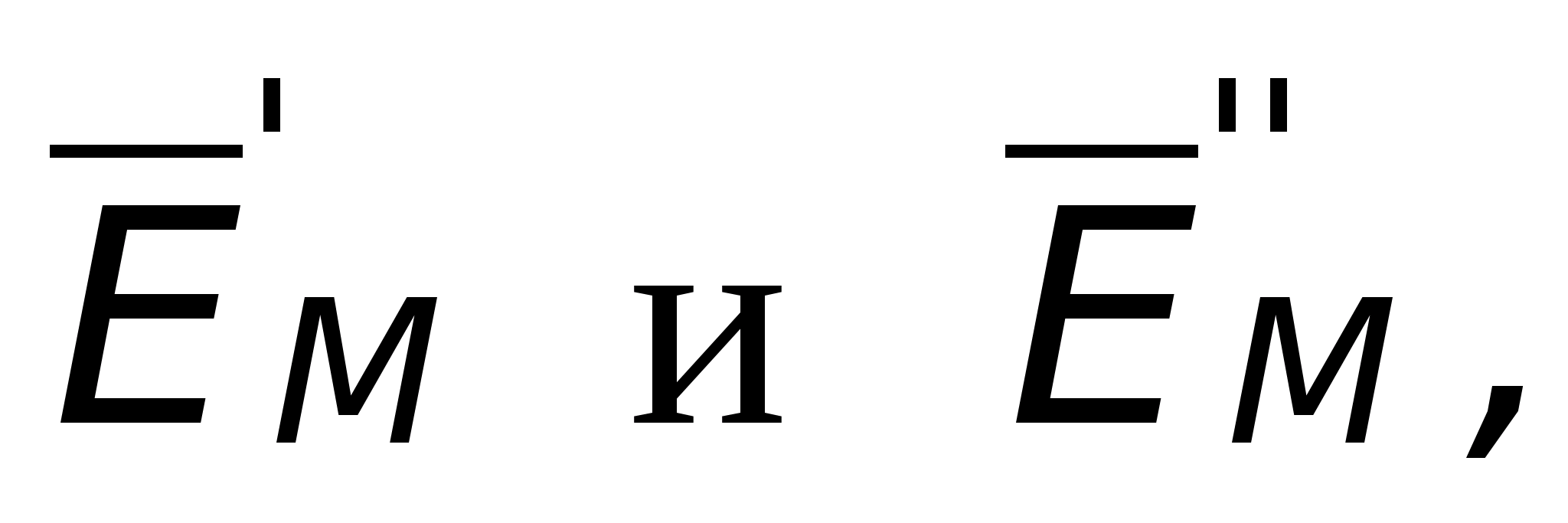 -
составляющие, создаваемые положительно
и отрицательно заряженной осью
соответственно. Величины
этих составляющих могут быть
определены по формулам, взятым из
предыдущей темы, а именно:
-
составляющие, создаваемые положительно
и отрицательно заряженной осью
соответственно. Величины
этих составляющих могут быть
определены по формулам, взятым из
предыдущей темы, а именно:
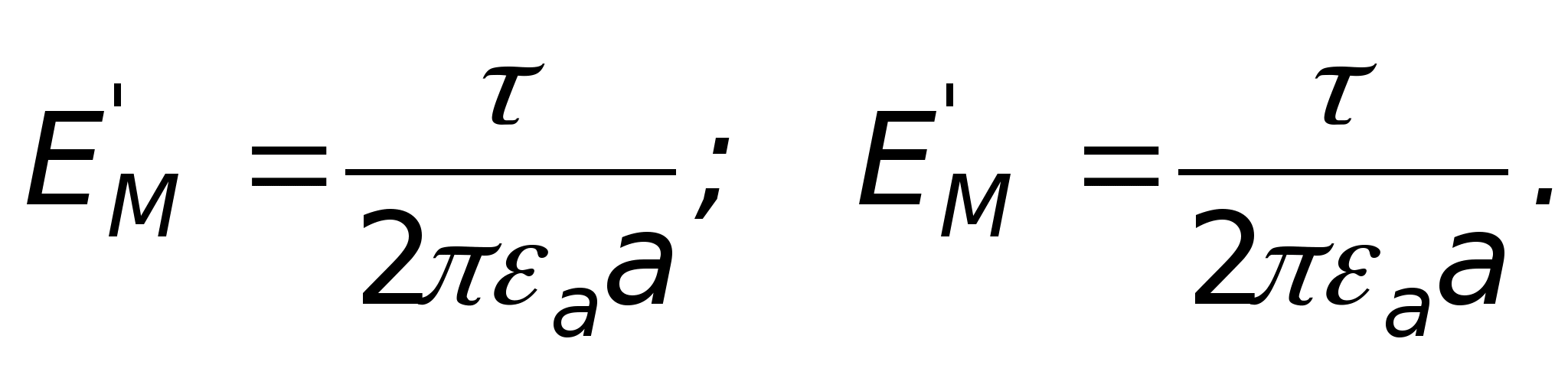 Аналогично для потенциала
Аналогично для потенциала
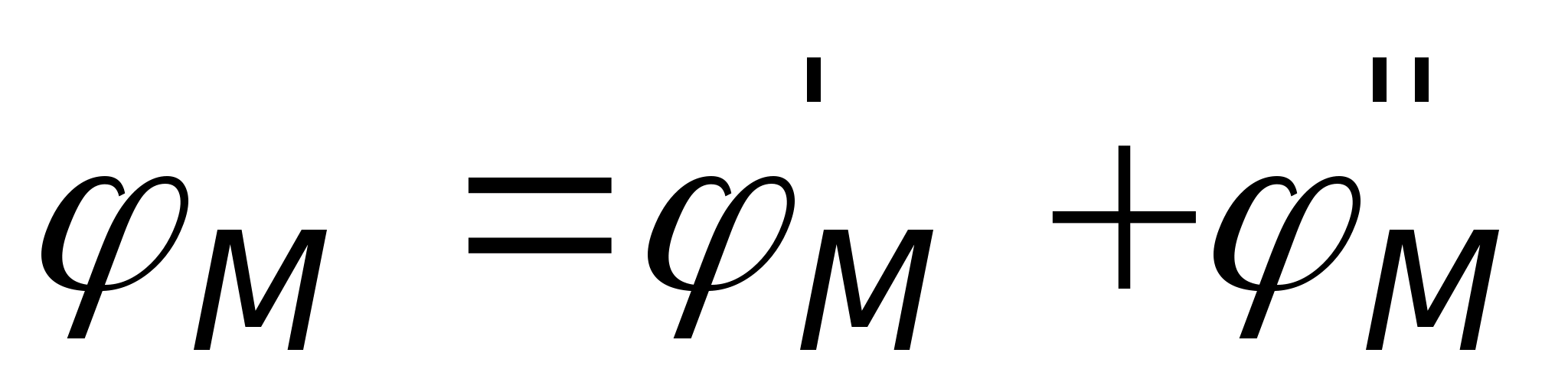 ,
где
.
Тогда
Из последнего выражения следует, что
совокупность точек, для которых
,
где
.
Тогда
Из последнего выражения следует, что
совокупность точек, для которых
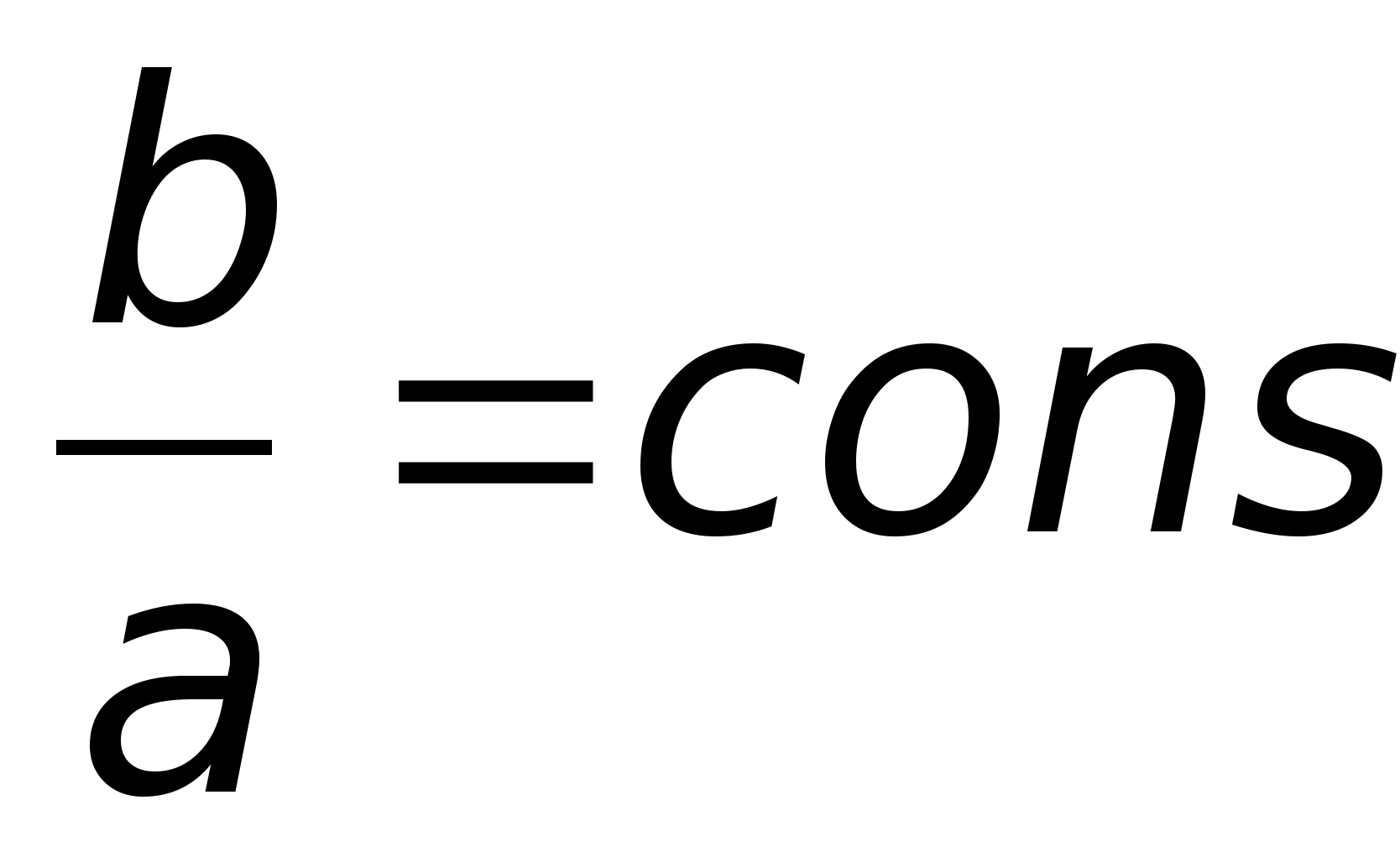 ,
представляет собой эквипотенциаль. Из
геометрии известно, что геометрическим
местом точек, отношение расстояний от
которых до двух заданных точек является
величиной постоянной, есть окружность
(теорема Аполлония). Поэтому эквипотенциали
в поле двух заряженных осей являются
окружностями. Для построения
эквипотенциальной линии, проходящей
через точку М
, проводим биссектрисы
внутреннего аМ
b
н внешнего рМа
углов. Точки пересечения
этих биссектрис с линией, проведенной
через оси, (т.1 и т.2), а также т. М
являются тремя точками этой эквипотенциали.
Центр этой окружности находится в точке,
расположенной посредине между т.1 и т.2.
,
представляет собой эквипотенциаль. Из
геометрии известно, что геометрическим
местом точек, отношение расстояний от
которых до двух заданных точек является
величиной постоянной, есть окружность
(теорема Аполлония). Поэтому эквипотенциали
в поле двух заряженных осей являются
окружностями. Для построения
эквипотенциальной линии, проходящей
через точку М
, проводим биссектрисы
внутреннего аМ
b
н внешнего рМа
углов. Точки пересечения
этих биссектрис с линией, проведенной
через оси, (т.1 и т.2), а также т. М
являются тремя точками этой эквипотенциали.
Центр этой окружности находится в точке,
расположенной посредине между т.1 и т.2.
Электростатическое поле и ёмкость двухпроводной линии электропередачи (ЛЭП)
П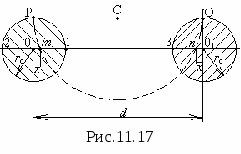 усть
провода ЛЭП имеют одинаковый радиус
r
о
,
расположены на
расстоянии d
друг от друга и находятся в среде
с проницаемостью ε а (рис.11.17).
Если левому проводу сообщен заряд
τ
на единицу длины, правому -τ
,
то в пространстве между проводами
возникнет электростатическое поле,
которое можно представить в виде части
поля двух заряденных осей. Действительно,
поскольку провода металлические, то
внутри них поля нет (Е
=0), а потенциал
всех точек каждого провода одинаков,
т.е. поверхность каждого провода является
эквипотенциальной. Поэтому две заряженные
оси, расположенные в т. m
и n,
создадут
такую же картину поля как и двухпроводная
ЛЭП, если т. m
и n
расположить
так, чтобы поверхности проводов
были для них эквипотенциалями. Точки
m
и n
принято называть
электрическими осями в отличие от
геометрических осей (точки О и О 1).
Смещение электрических и геометрических
осей (x
) в силу симметрии
одинаково в левом и правом проводе. Для
определения величины x
возьмём точки 1 и 2 и запишем выражения
потенциалов этих точек в поле двух
заряженных осей, расположенных в т. m
и n
.
усть
провода ЛЭП имеют одинаковый радиус
r
о
,
расположены на
расстоянии d
друг от друга и находятся в среде
с проницаемостью ε а (рис.11.17).
Если левому проводу сообщен заряд
τ
на единицу длины, правому -τ
,
то в пространстве между проводами
возникнет электростатическое поле,
которое можно представить в виде части
поля двух заряденных осей. Действительно,
поскольку провода металлические, то
внутри них поля нет (Е
=0), а потенциал
всех точек каждого провода одинаков,
т.е. поверхность каждого провода является
эквипотенциальной. Поэтому две заряженные
оси, расположенные в т. m
и n,
создадут
такую же картину поля как и двухпроводная
ЛЭП, если т. m
и n
расположить
так, чтобы поверхности проводов
были для них эквипотенциалями. Точки
m
и n
принято называть
электрическими осями в отличие от
геометрических осей (точки О и О 1).
Смещение электрических и геометрических
осей (x
) в силу симметрии
одинаково в левом и правом проводе. Для
определения величины x
возьмём точки 1 и 2 и запишем выражения
потенциалов этих точек в поле двух
заряженных осей, расположенных в т. m
и n
.
Так как т. 1 и 2 расположены на
поверхности одного и того же провода,
то φ 1 =φ 2 , следовательно,
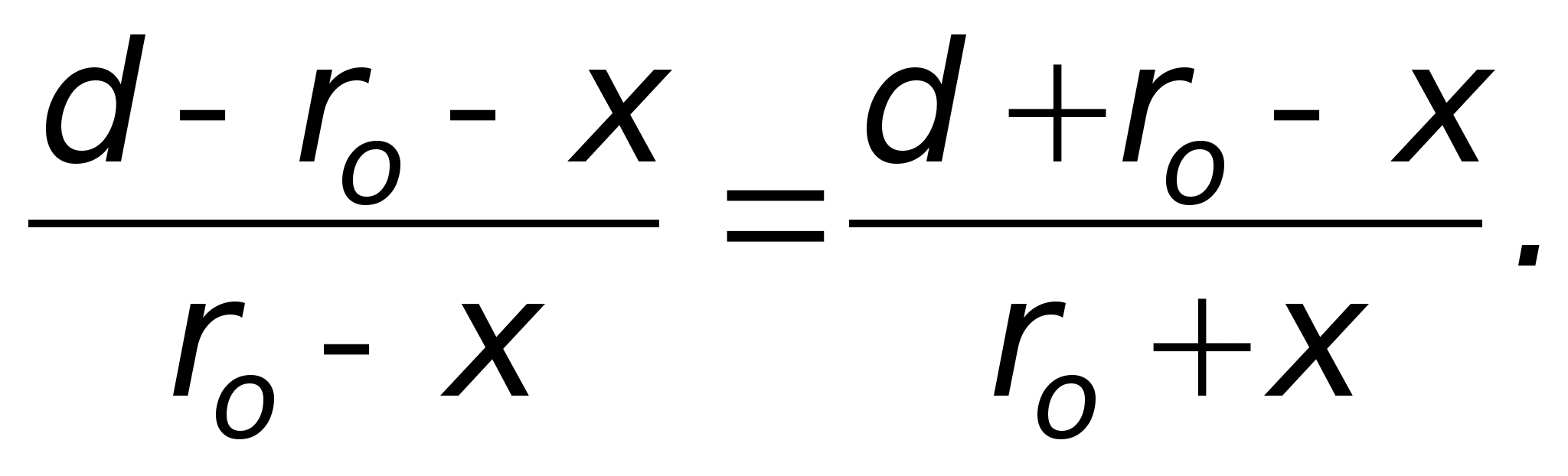 Решая это равенство относительно x
,
получим
Решая это равенство относительно x
,
получим
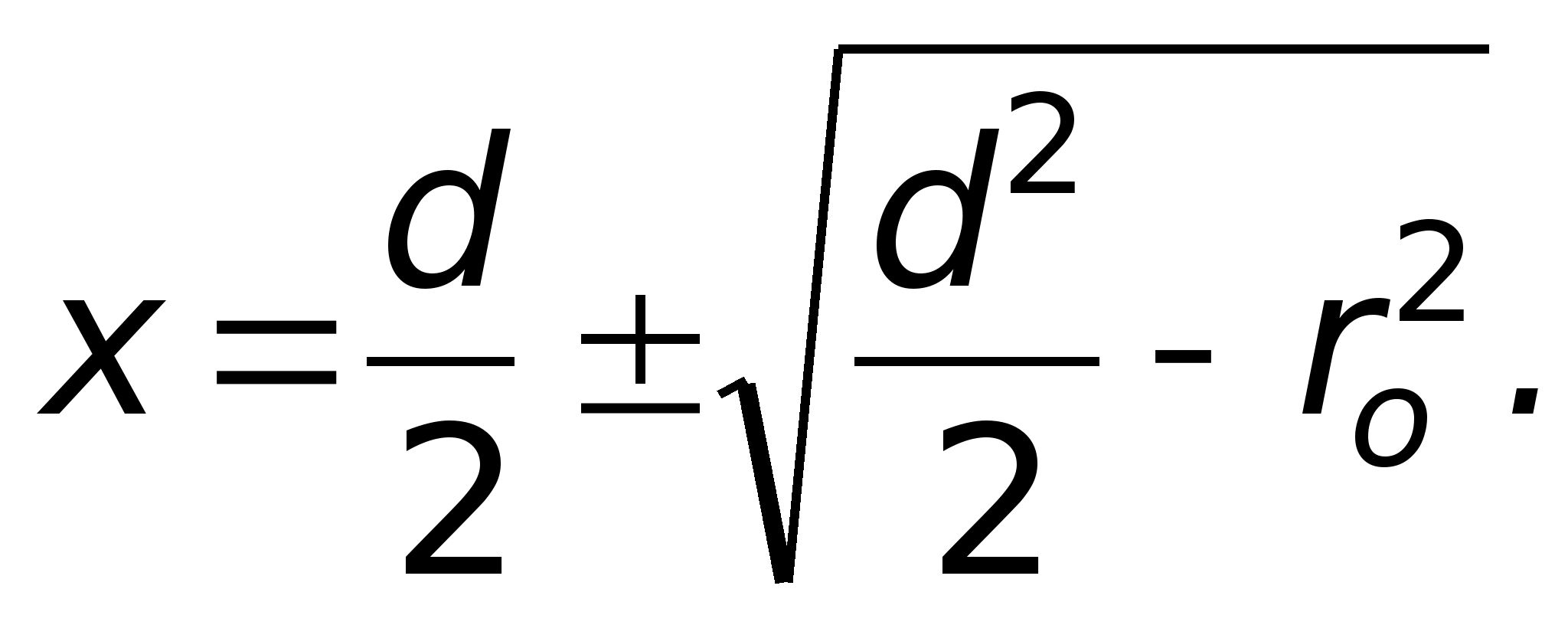 В этом выражении при отсчете x
от т.О плюс определяет положение т.
n
, а минус –
положение т. m
.
Если d>>r
o
,
то x
1 =0,
x
2 =d
,
т.е. электрические и геометрические
оси совпадают (нет смещения осей). Часто
x
не вычисляют
по полученной выше формуле, а получают
графическим путем. Для этого проводят
общую касательную к поверхности
проводников, делят расстояние между
точками касания (P и Q)
пополам (т. С) и проводят дугу окружности,
проходящей через т. Р и Q и
имеющей центр в т. С. Точки пересечения
этой окружности с линией О 1 О дают
положение электрических осей. Из
геометрического определения положения
электрических осей так же видно, что
при d>>r
o
т.
m
и n
сольются с т. О и О 1 .
В этом выражении при отсчете x
от т.О плюс определяет положение т.
n
, а минус –
положение т. m
.
Если d>>r
o
,
то x
1 =0,
x
2 =d
,
т.е. электрические и геометрические
оси совпадают (нет смещения осей). Часто
x
не вычисляют
по полученной выше формуле, а получают
графическим путем. Для этого проводят
общую касательную к поверхности
проводников, делят расстояние между
точками касания (P и Q)
пополам (т. С) и проводят дугу окружности,
проходящей через т. Р и Q и
имеющей центр в т. С. Точки пересечения
этой окружности с линией О 1 О дают
положение электрических осей. Из
геометрического определения положения
электрических осей так же видно, что
при d>>r
o
т.
m
и n
сольются с т. О и О 1 .
После того, как определено смещение осей, задача сведена к предыдущей.
Перейдем к вопросу о
ёмкости двухпроводной линии. Если два
проводника разделены диэлектриком и
несут на себе равные по величине и
противоположные по знаку заряды, то в
пространстве между ними создается
электростатическое поле. Пусть напряжение
между проводниками равно U
.
Тогда ёмкостью между проводниками
называется отношение абсолютной величины
заряда на одном из тел к напряжению
между ними:
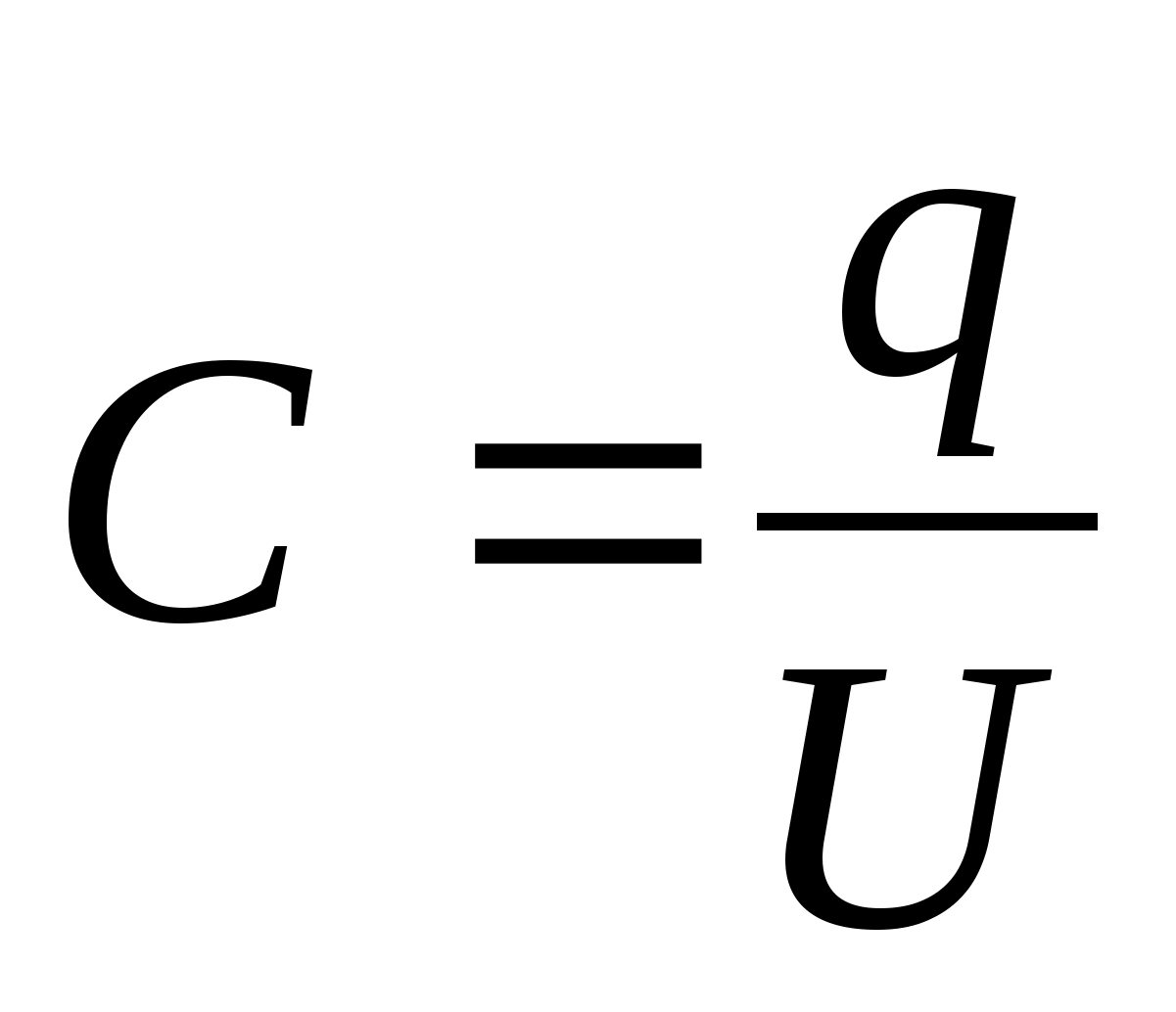 .
Единица измерения ёмкости – Фарада
(
.
Единица измерения ёмкости – Фарада
(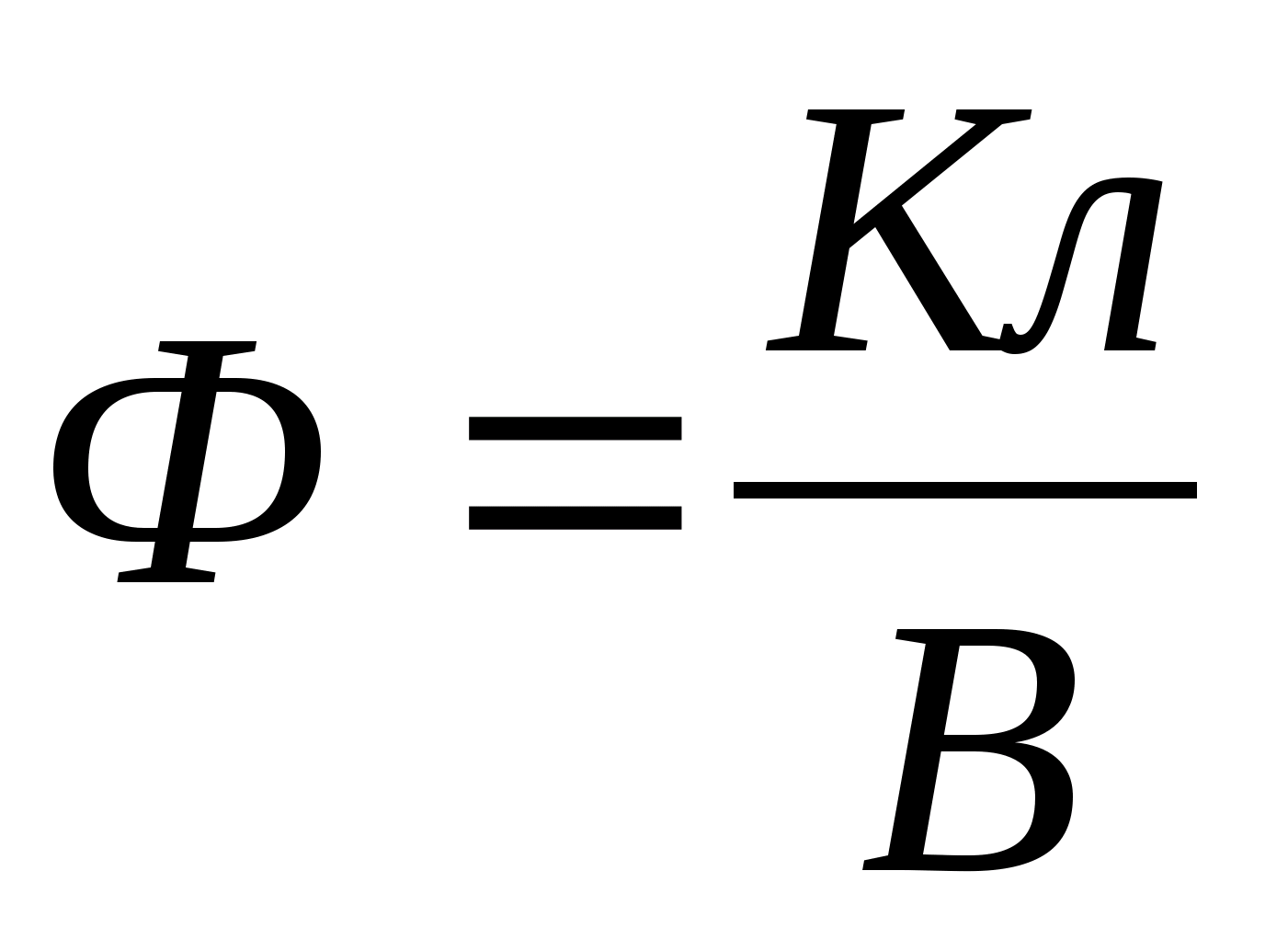 ).
Так как напряжение между телами
пропорционально заряду на них, то ёмкость
ни от заряда, ни от напряжения не зависит,
а зависит она от конфигурации и
геометрических размеров тел, их взаимного
расположения и от свойств диэлектрика,
в котором они находятся. Существуют
устройства, предназначенные для получения
определенной величины ёмкости – это
конденсаторы, однако ёмкостью обладают
не только конденсаторы, а всякие два
тела, способные нести на себе равные по
величине и противоположные по знаку
заряды.
).
Так как напряжение между телами
пропорционально заряду на них, то ёмкость
ни от заряда, ни от напряжения не зависит,
а зависит она от конфигурации и
геометрических размеров тел, их взаимного
расположения и от свойств диэлектрика,
в котором они находятся. Существуют
устройства, предназначенные для получения
определенной величины ёмкости – это
конденсаторы, однако ёмкостью обладают
не только конденсаторы, а всякие два
тела, способные нести на себе равные по
величине и противоположные по знаку
заряды.
Определим ёмкость двухпроводной
линии. Напряжение между проводами
Заряд одного из проводов q=τl
.
Тогда
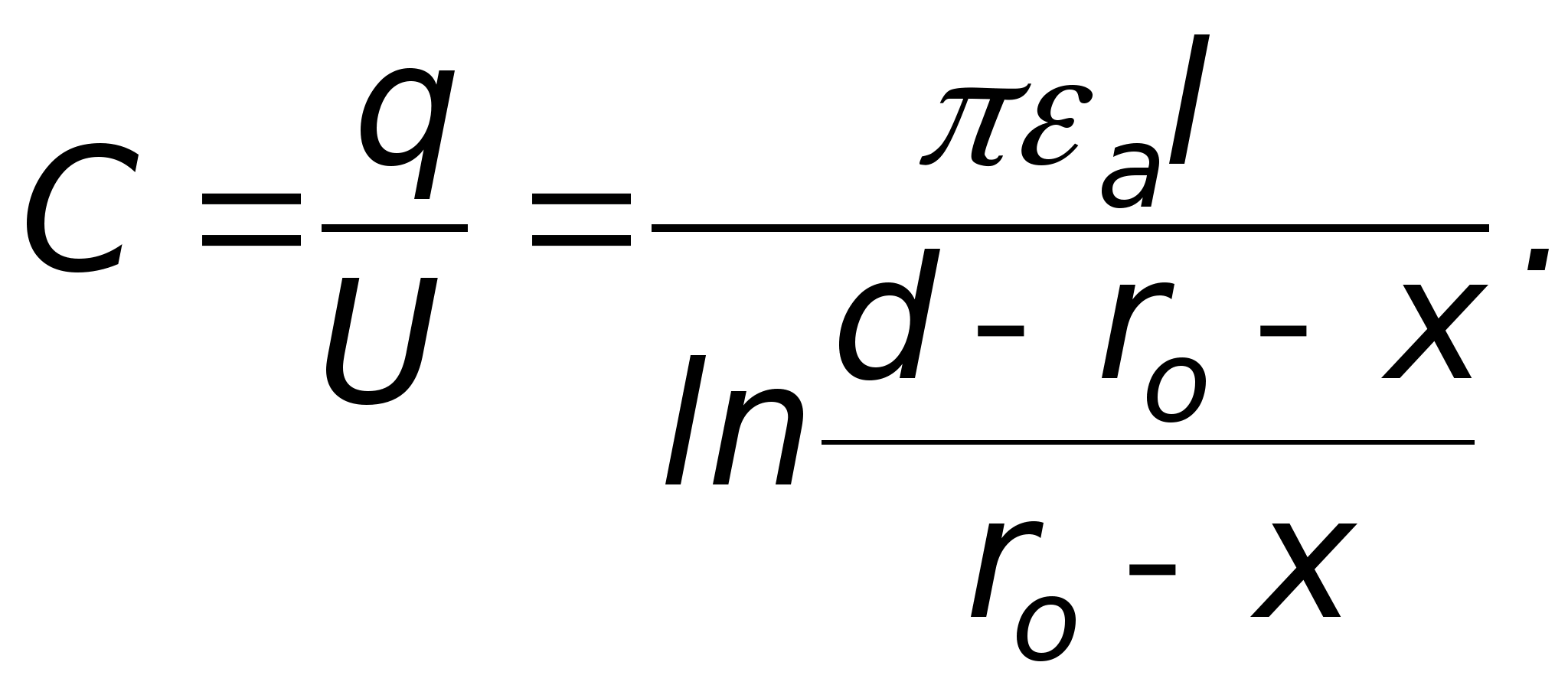 Часто определяют ёмкость единицы длины
линии
Часто определяют ёмкость единицы длины
линии
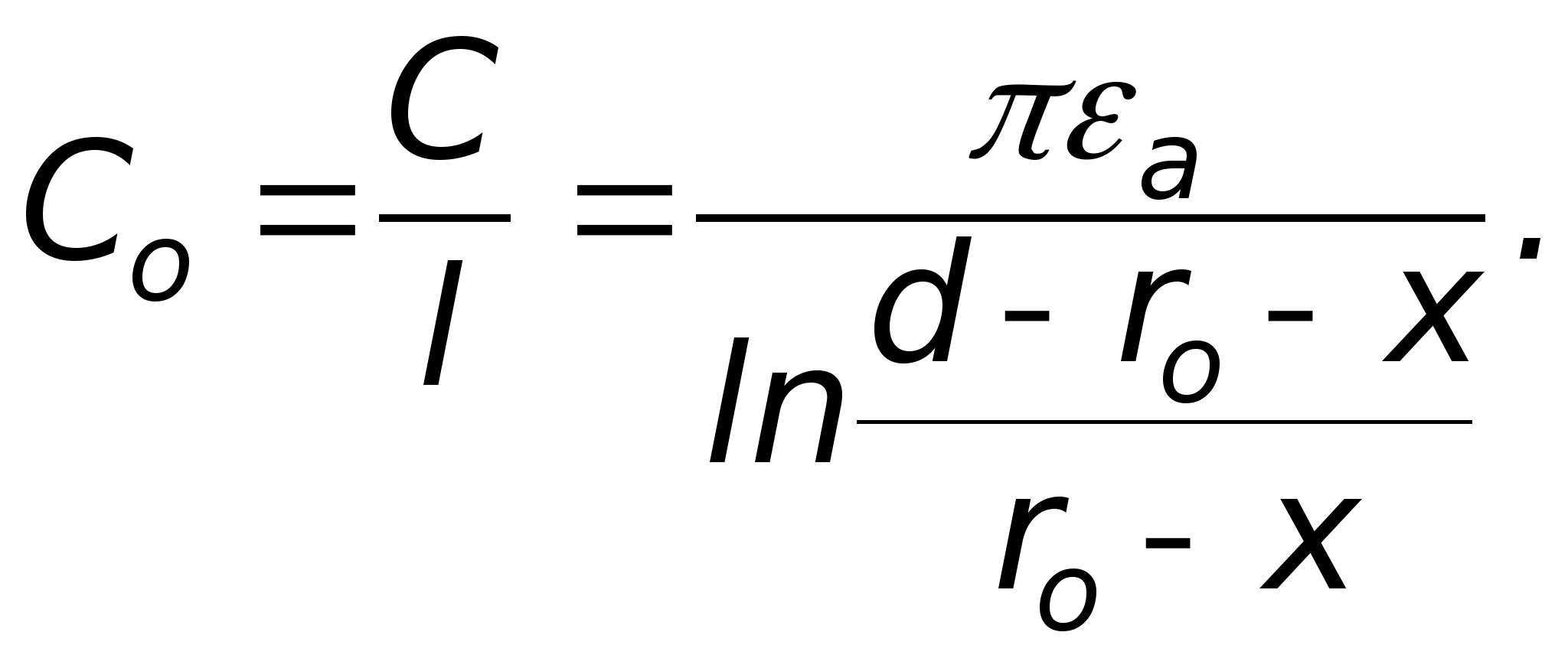 А если d>>r
o ,
то x
=0
и
А если d>>r
o ,
то x
=0
и
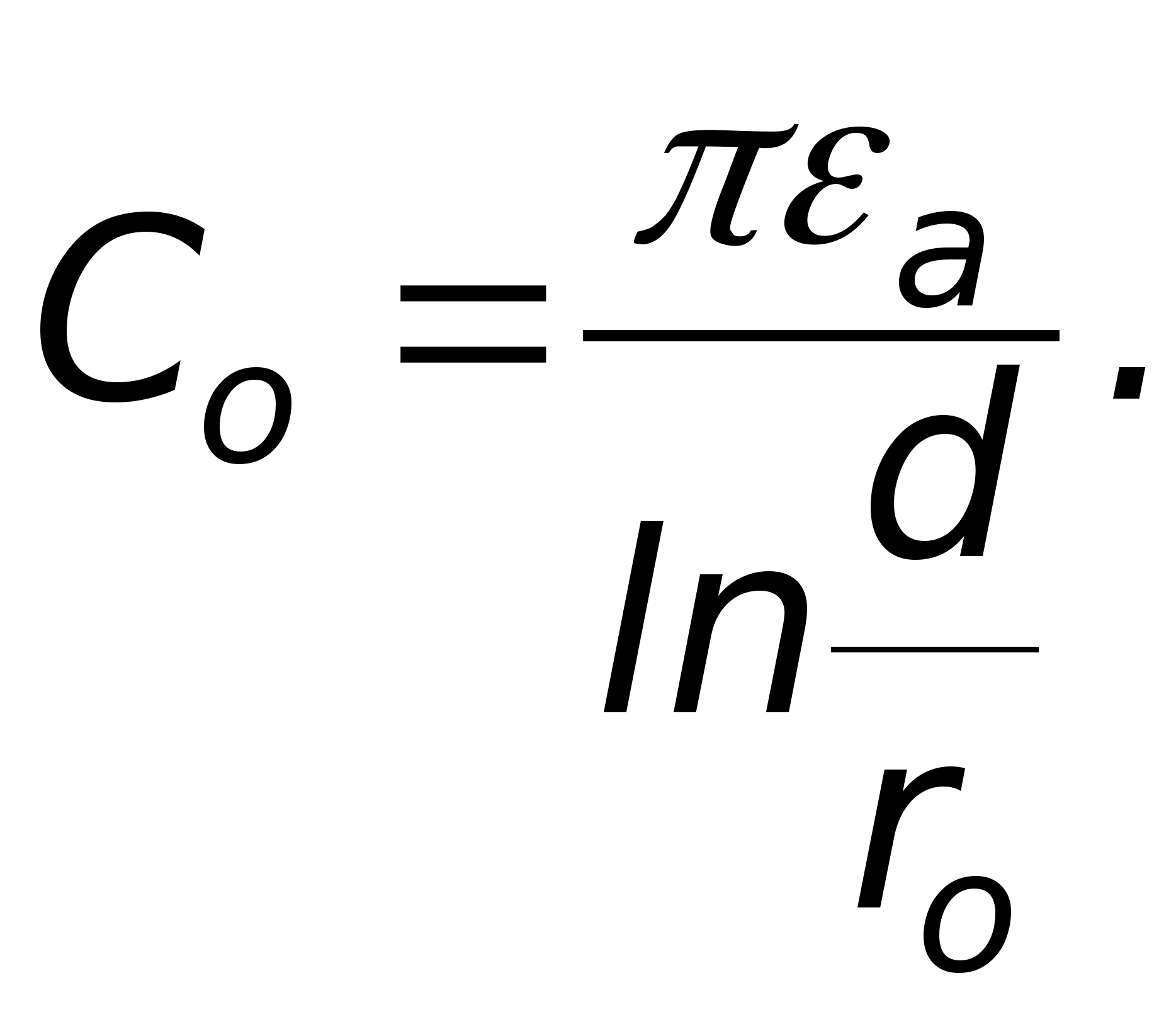 Из полученных формул видно, что ёмкость
действительно зависит от размеров линии
и свойств среды, в которой находятся
провода, в частности, если увеличивать
расстояние d
между проводами, то ёмкость будет
уменьшаться.
Из полученных формул видно, что ёмкость
действительно зависит от размеров линии
и свойств среды, в которой находятся
провода, в частности, если увеличивать
расстояние d
между проводами, то ёмкость будет
уменьшаться.
Электростатическое поле и ёмкость коаксиального кабеля
К оаксиальный
кабель представляет собой два металлических
соосных цилиндра, расположенных один
внутри другого и изолированных друг от
друга диэлектриком с проницаемостью
ε
а
(рис.11.18). Такой
кабель широко применяется на высоких
частотах. Пусть внутренний цилиндр,
который называется жилой, несёт на себе
заряд +τ
, а наружный цилиндр (оболочка)
– заряд –τ
. Тогда возникнет
электростатическое поле, расчёт которого
произведём для отдельных областей
кабеля. Внутри жилы (0>r>r
1)
поля нет, так как жила проводящая,
т.е. E
=0,
φ
=const.
Для определения напряжённости поля
в пространстве между жилой и оболочкой
воспользуемся теоремой Гаусса:
оаксиальный
кабель представляет собой два металлических
соосных цилиндра, расположенных один
внутри другого и изолированных друг от
друга диэлектриком с проницаемостью
ε
а
(рис.11.18). Такой
кабель широко применяется на высоких
частотах. Пусть внутренний цилиндр,
который называется жилой, несёт на себе
заряд +τ
, а наружный цилиндр (оболочка)
– заряд –τ
. Тогда возникнет
электростатическое поле, расчёт которого
произведём для отдельных областей
кабеля. Внутри жилы (0>r>r
1)
поля нет, так как жила проводящая,
т.е. E
=0,
φ
=const.
Для определения напряжённости поля
в пространстве между жилой и оболочкой
воспользуемся теоремой Гаусса:
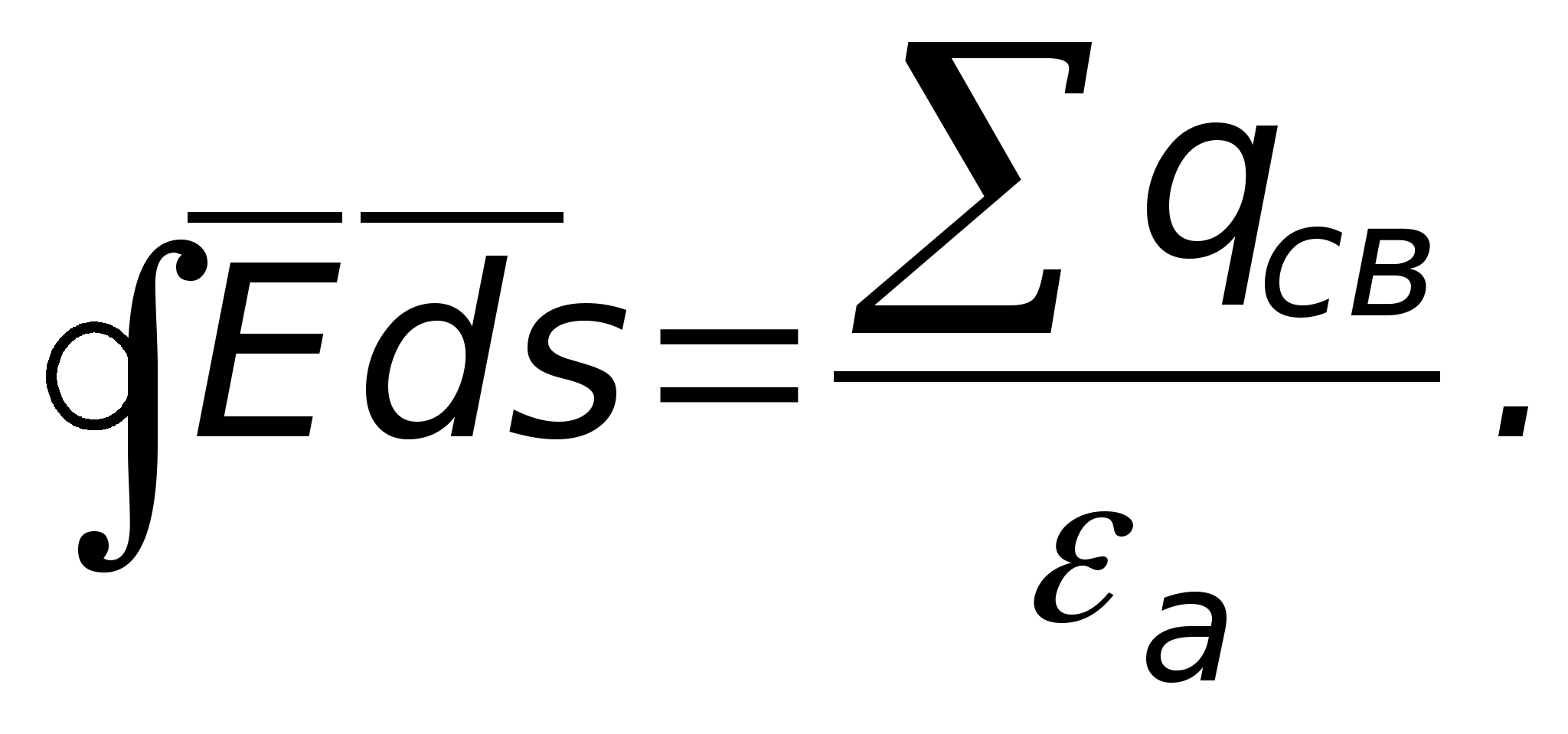 В качестве поверхности интегрирования
возьмём цилиндр радиуса r
и длиной l
.
Поток вектора Е
через донышки
этого цилиндра равен нулю (векторы Е
и ds
перпендикулярны), а через его боковую
поверхность
В качестве поверхности интегрирования
возьмём цилиндр радиуса r
и длиной l
.
Поток вектора Е
через донышки
этого цилиндра равен нулю (векторы Е
и ds
перпендикулярны), а через его боковую
поверхность
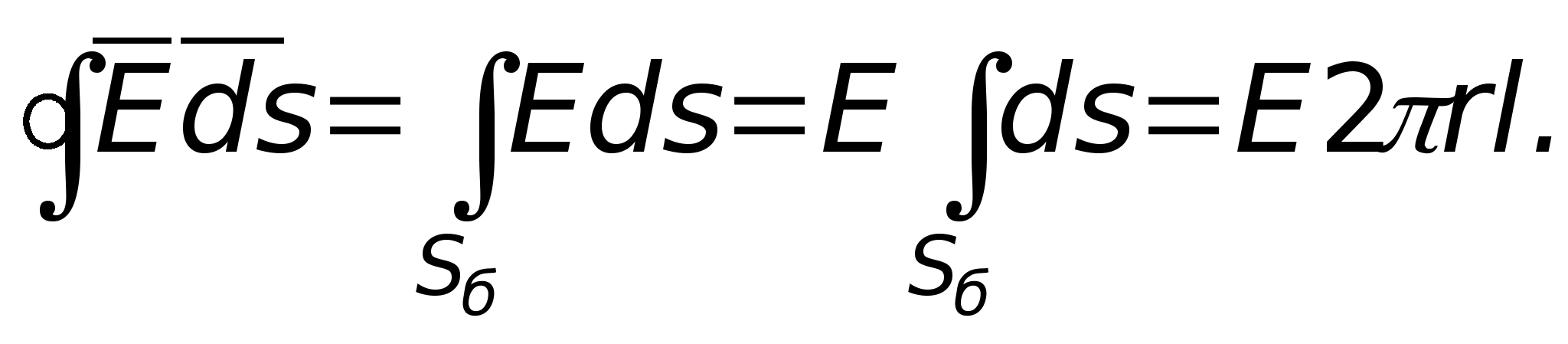
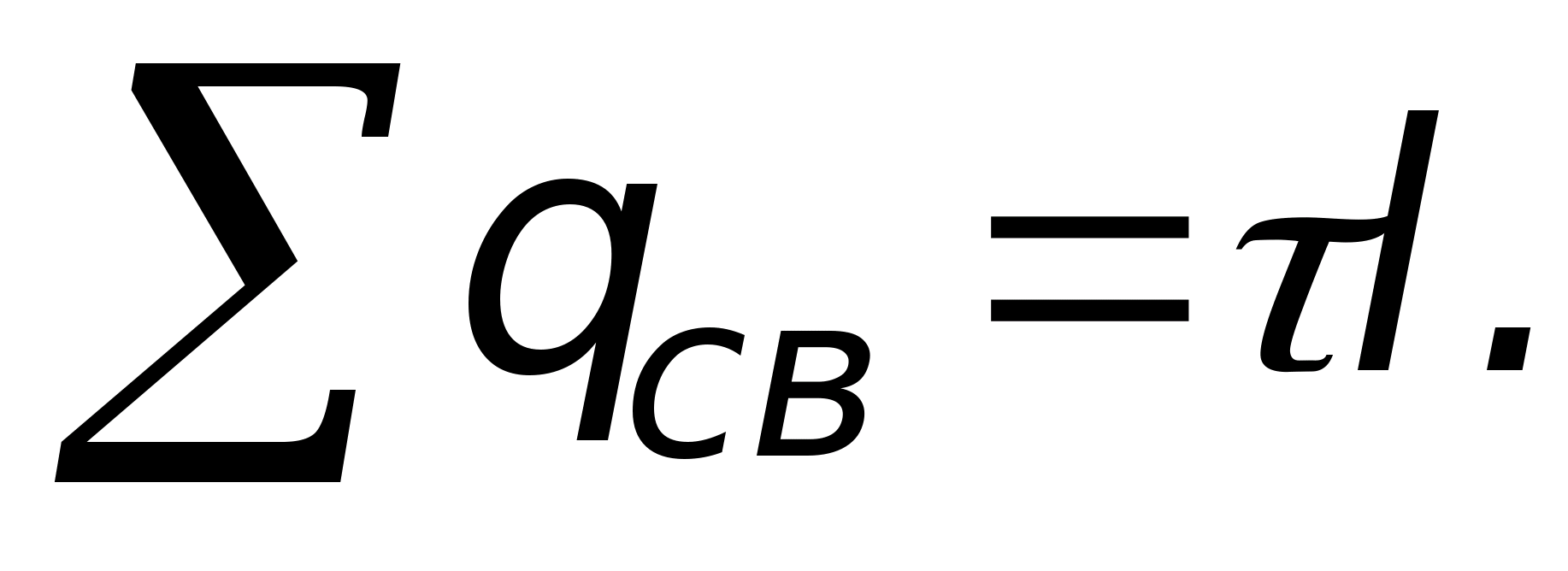 Тогда
Тогда
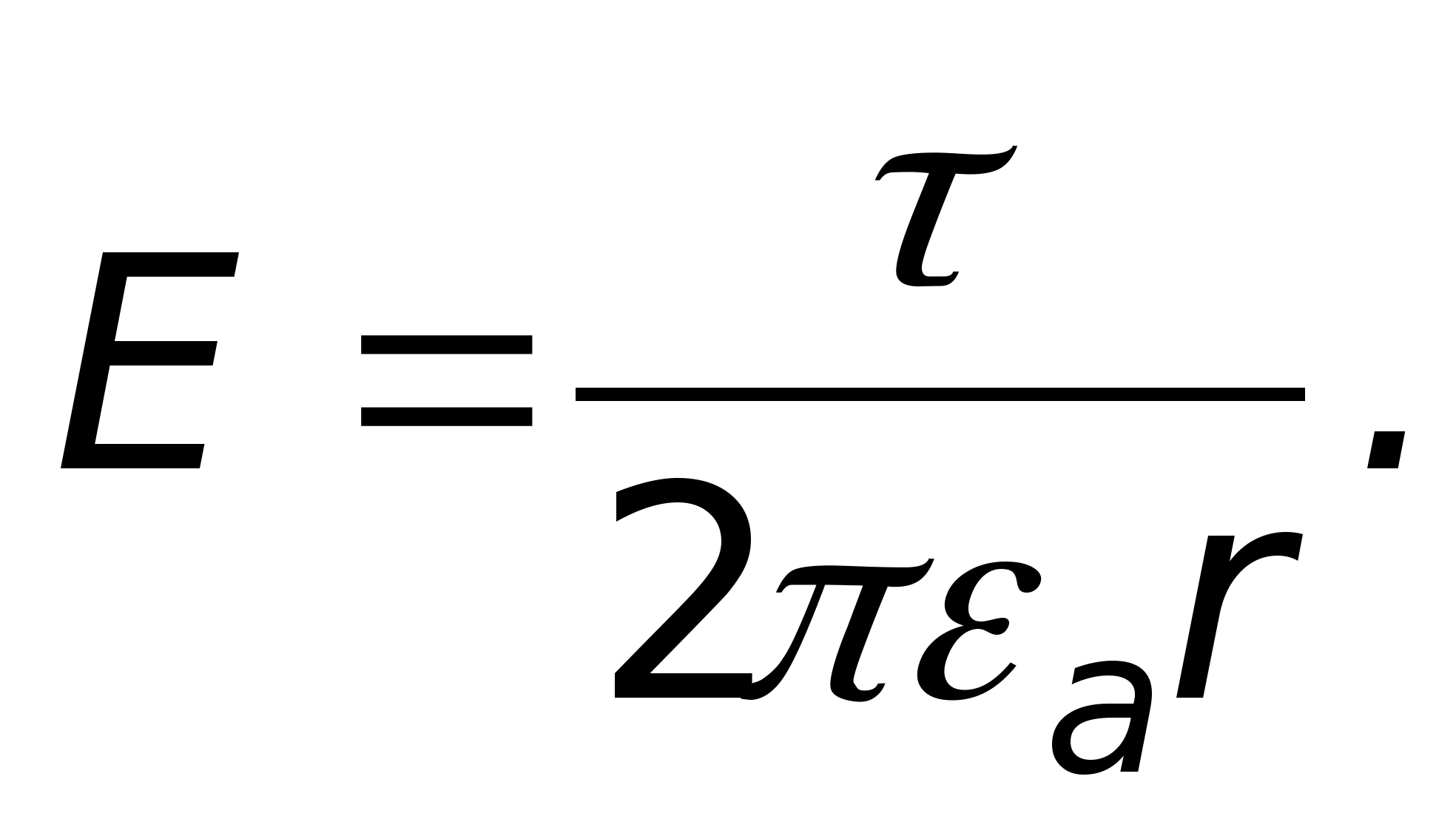 Так как Е
имеет только радиальную
составляющую, то
Так как Е
имеет только радиальную
составляющую, то
Для всех точек оболочки кабеля (r 2 3) E =0, φ =const, так как она проводящая. За пределами кабеля (r 3 поэтому E =0, φ =const. Таким образом в данном устройстве поле имеется только в пространстве между жилой и оболочкой.
Ёмкость
коаксиального кабеля С
=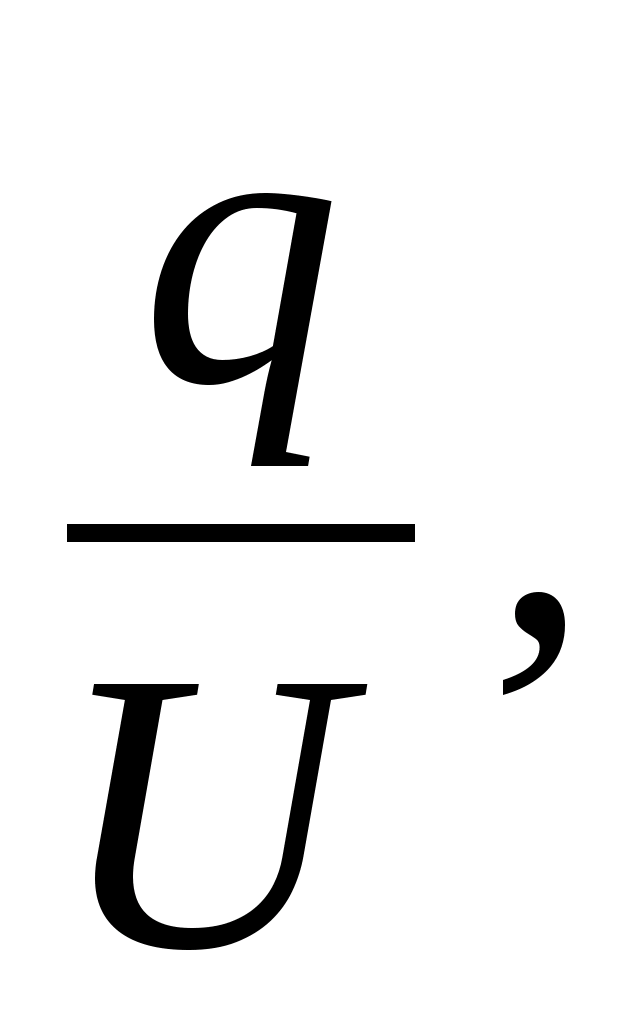 где q=τl
,
a
где q=τl
,
a
Тогда
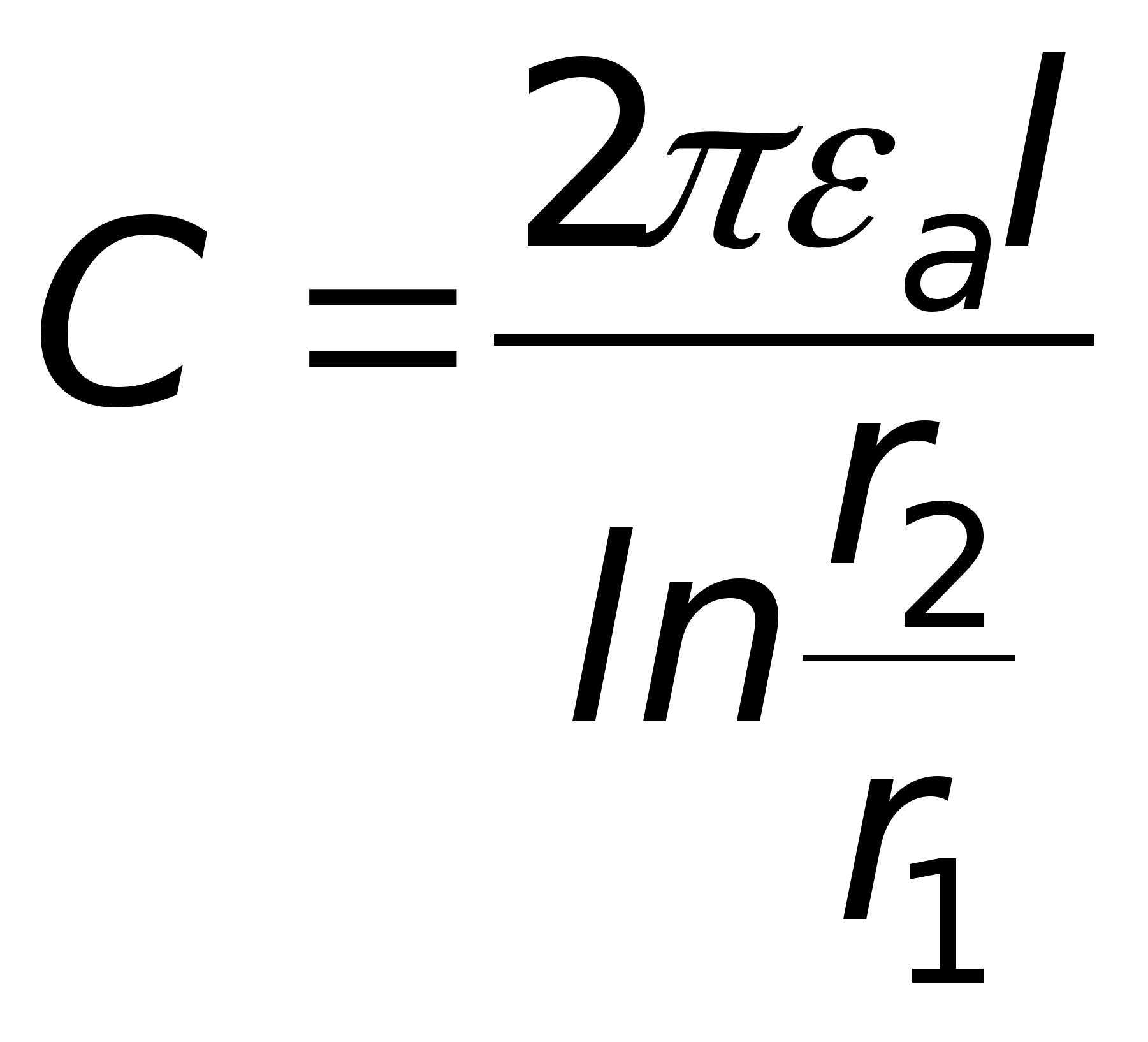 ,
а
,
а
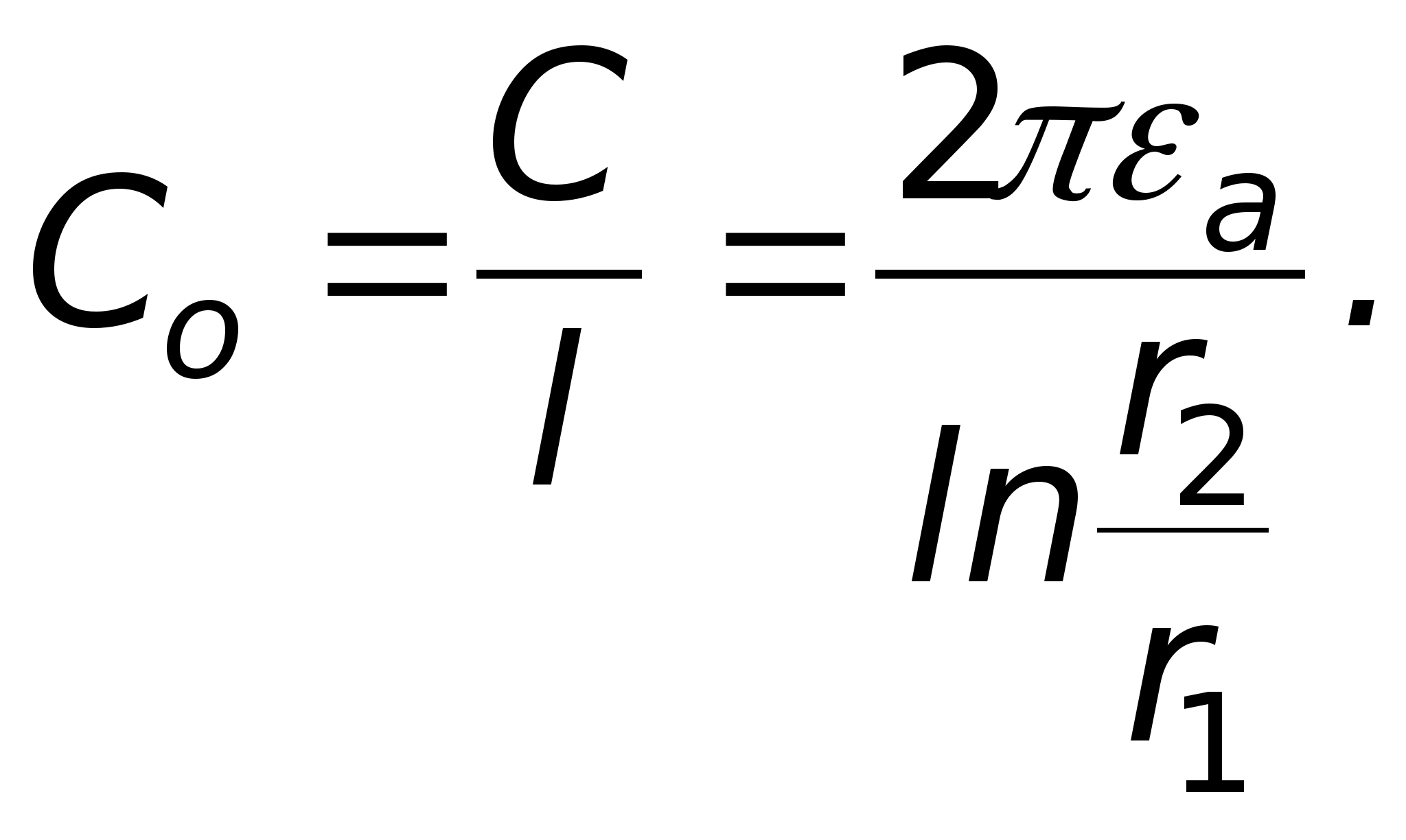
Электростатическое поле и ёмкость однослойного и двухслойного плоских конденсаторов
Однослойный плоский конденсатор
состоит из двух металлических пластин
сечением S
,
расположенных на расстоянии d
друг от друга (рис.11.19). Определим
закон изменения Е
, D
и φ
, если к нему подведено
напряжение U
.
Если размеры пластин (длина, высота)
намного больше d,
то можно пренебречь краевым эффектом
(искажением поля на краях пластин) и
считать его электростатическое поле
равномерным, т.е. при всех значениях х
напряженность поля одна и та же. Тогда
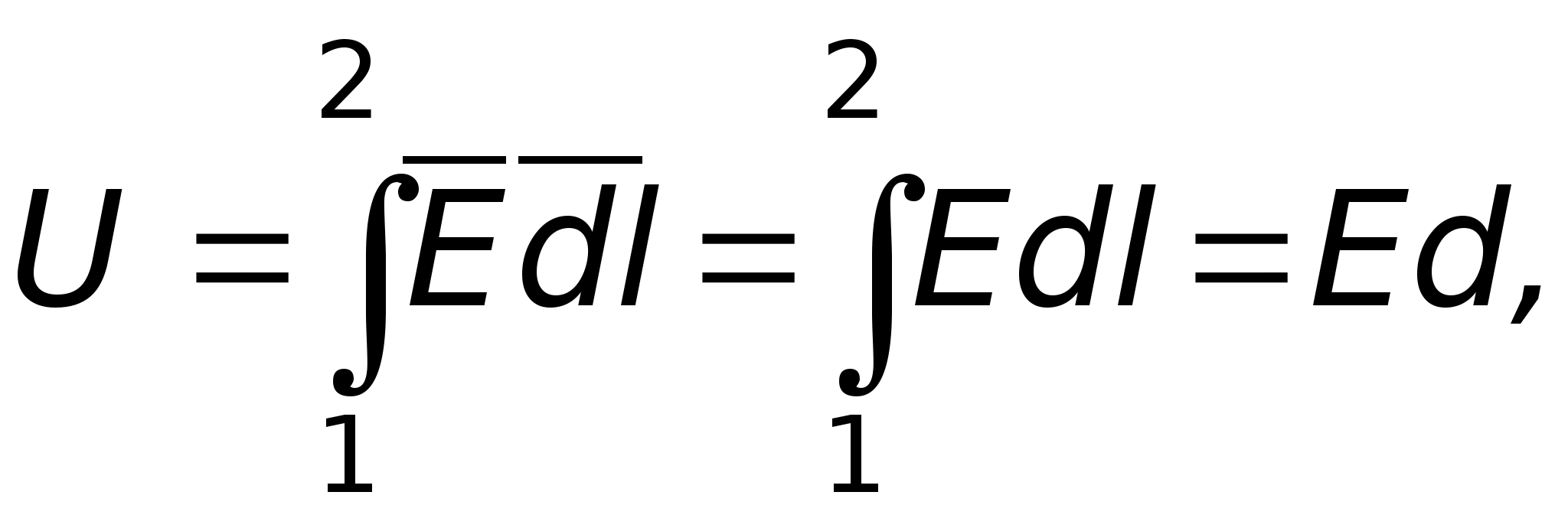 откуда
откуда
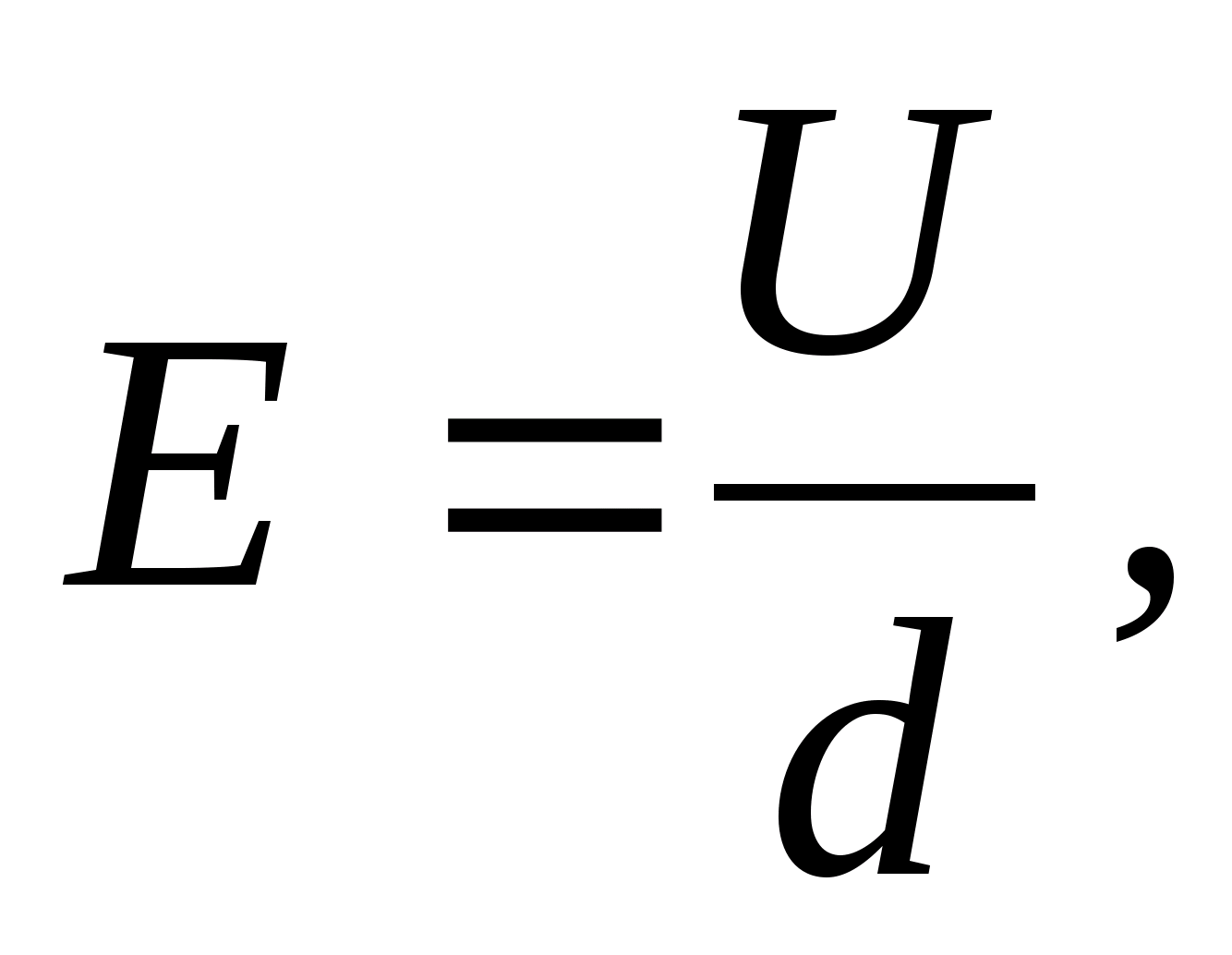 а D
=ε
a E=
а D
=ε
a E=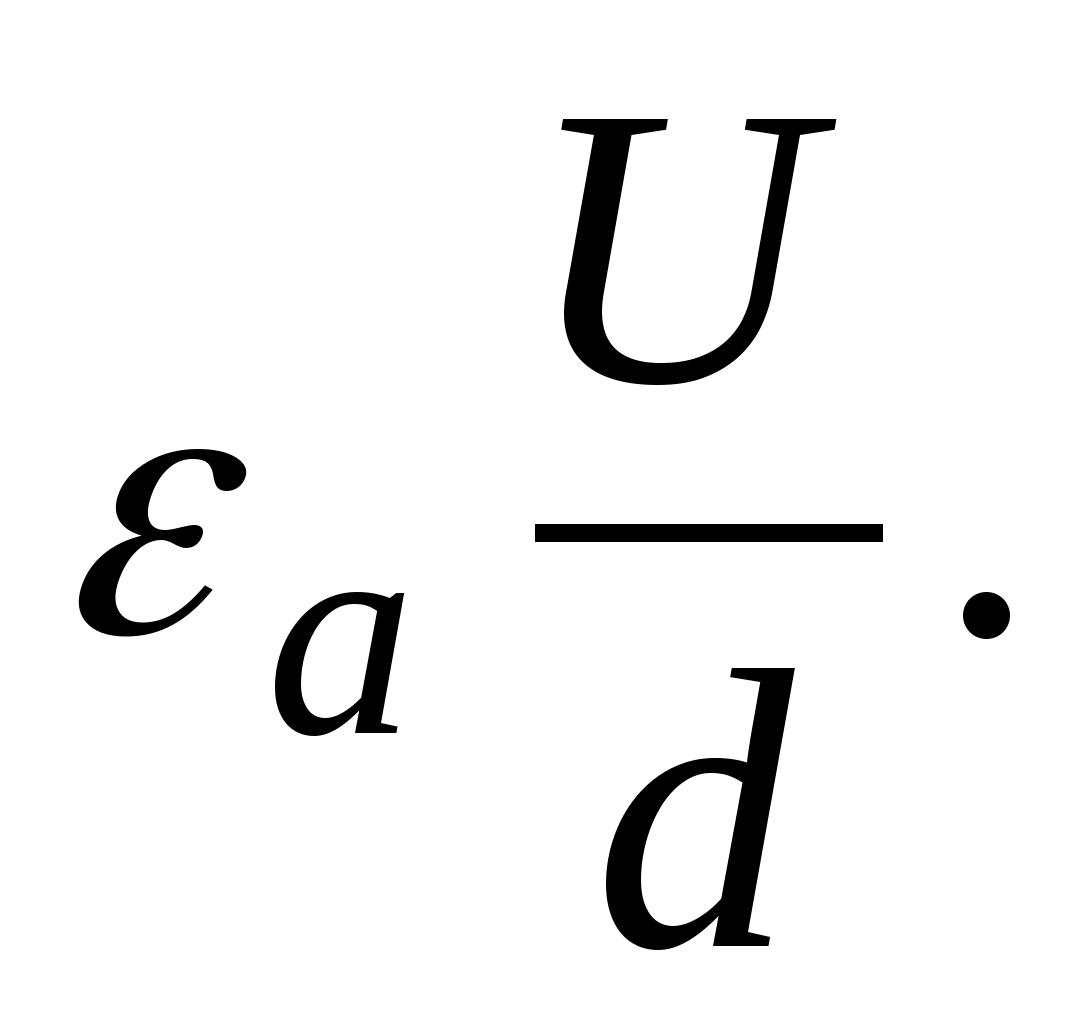 Так как
Так как
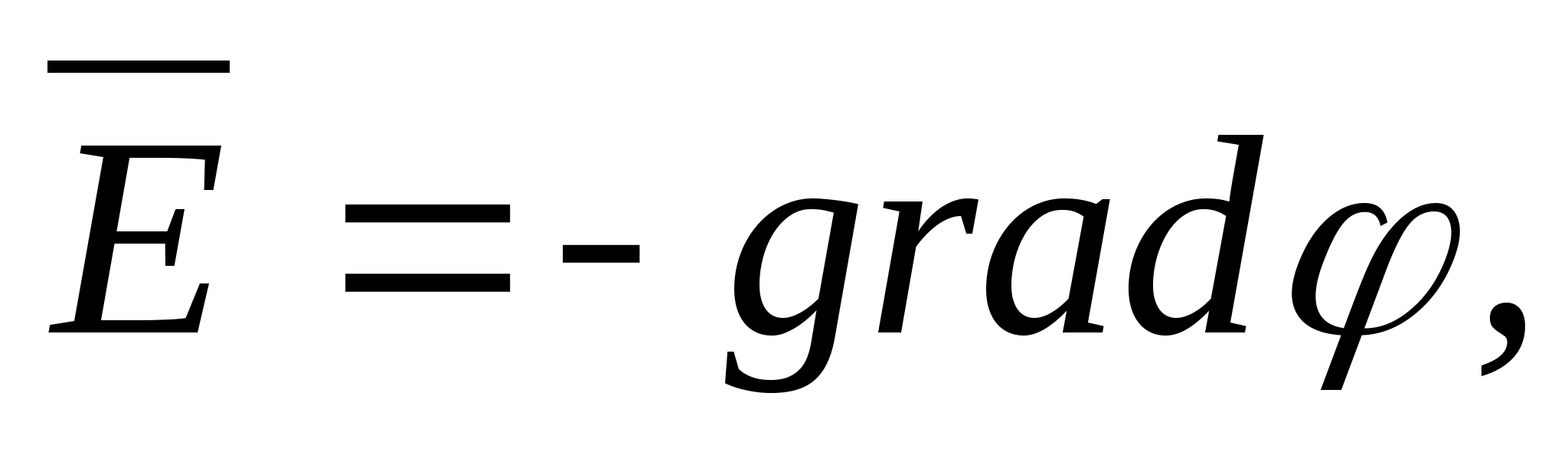 а φ
зависит только от х
(плоскость
yoz - эквипотенциаль), то
а φ
зависит только от х
(плоскость
yoz - эквипотенциаль), то
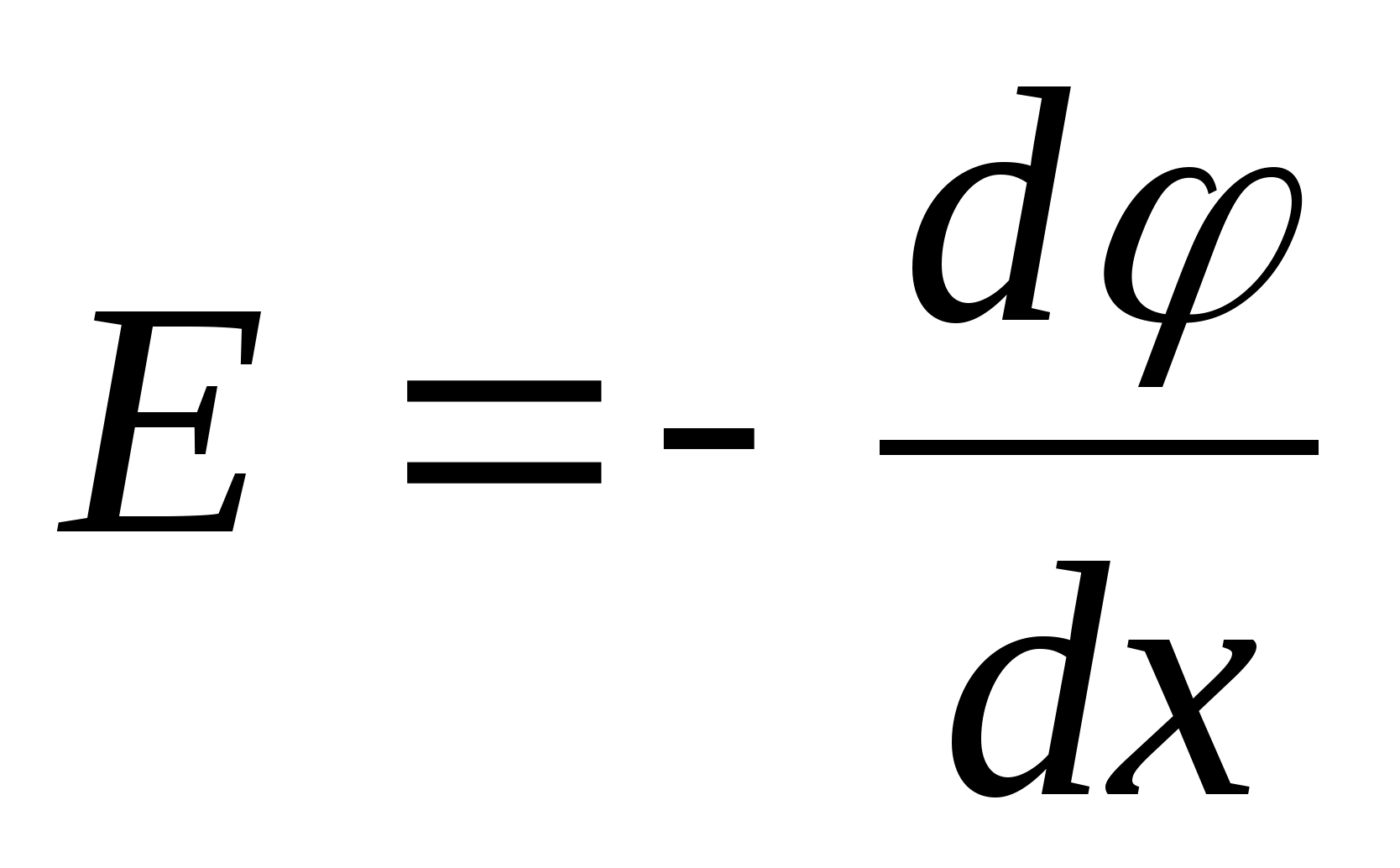 или
или
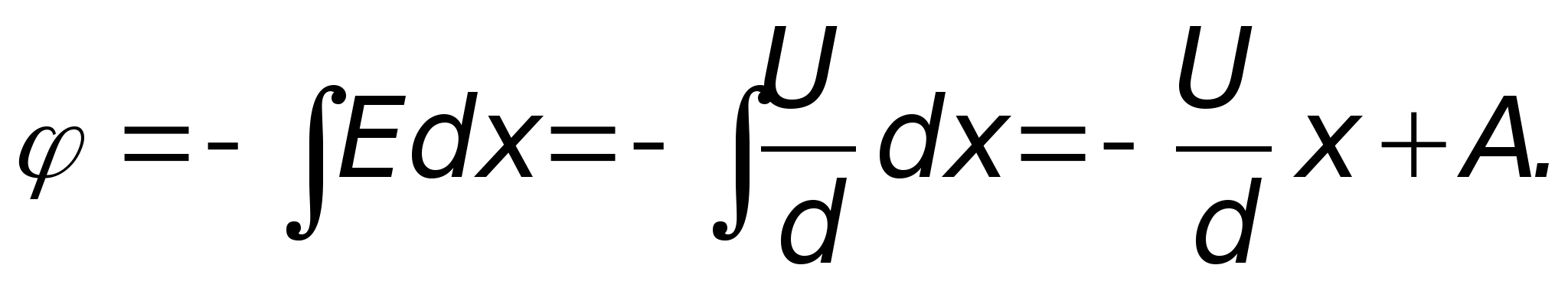 Для определения постоянной интегрирования
А
примем, что потенциал правой
пластины равен нулю, а левой равен U
,
т.е. при х
=0
φ=
U
.
Тогда А=
U
и
Для определения постоянной интегрирования
А
примем, что потенциал правой
пластины равен нулю, а левой равен U
,
т.е. при х
=0
φ=
U
.
Тогда А=
U
и
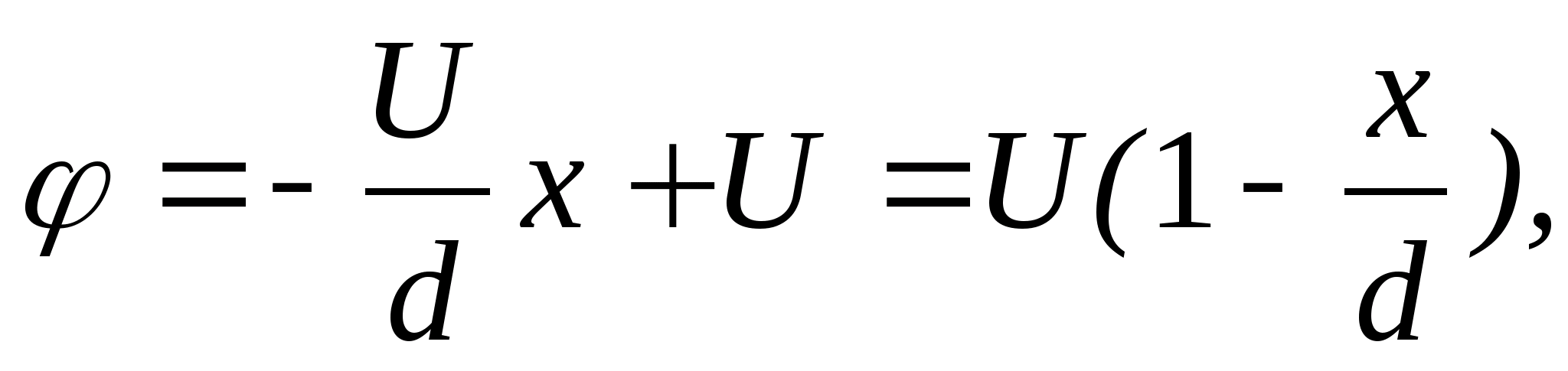 т.е. φ
изменяется по линейному закону
в зависимости от х
.
т.е. φ
изменяется по линейному закону
в зависимости от х
.
Определим ёмкость
плоского конденсатора
С
=
где U=Ed.
Для определения заряда, например,
левой пластины воспользуемся теоремой
Гаусса:
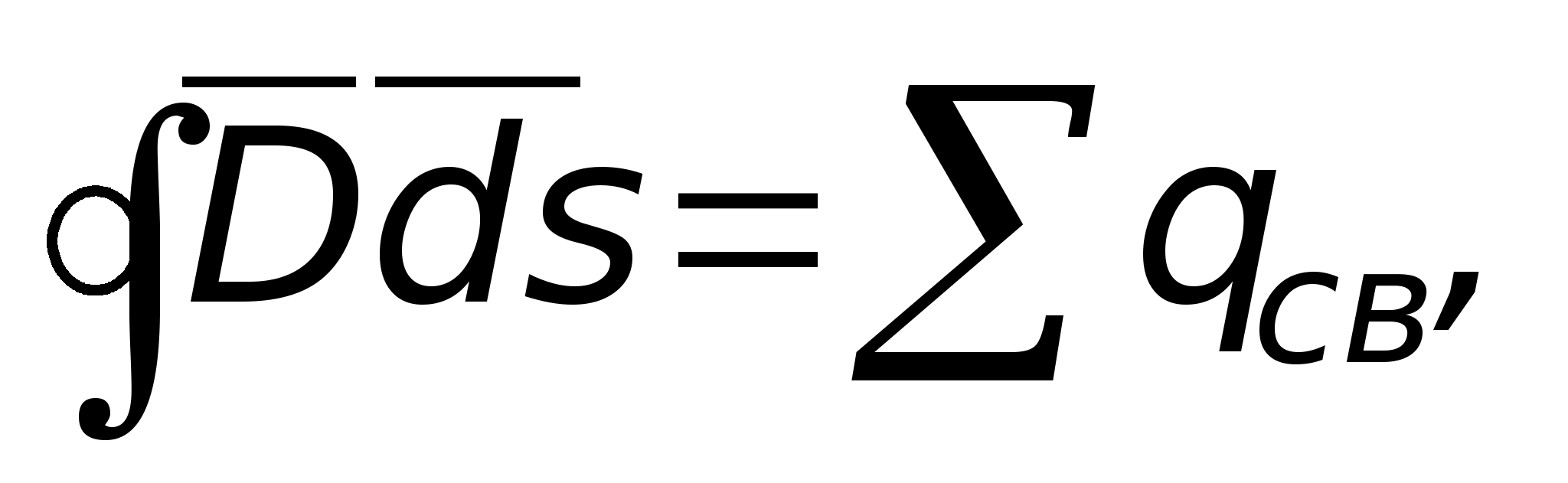 причем
причем
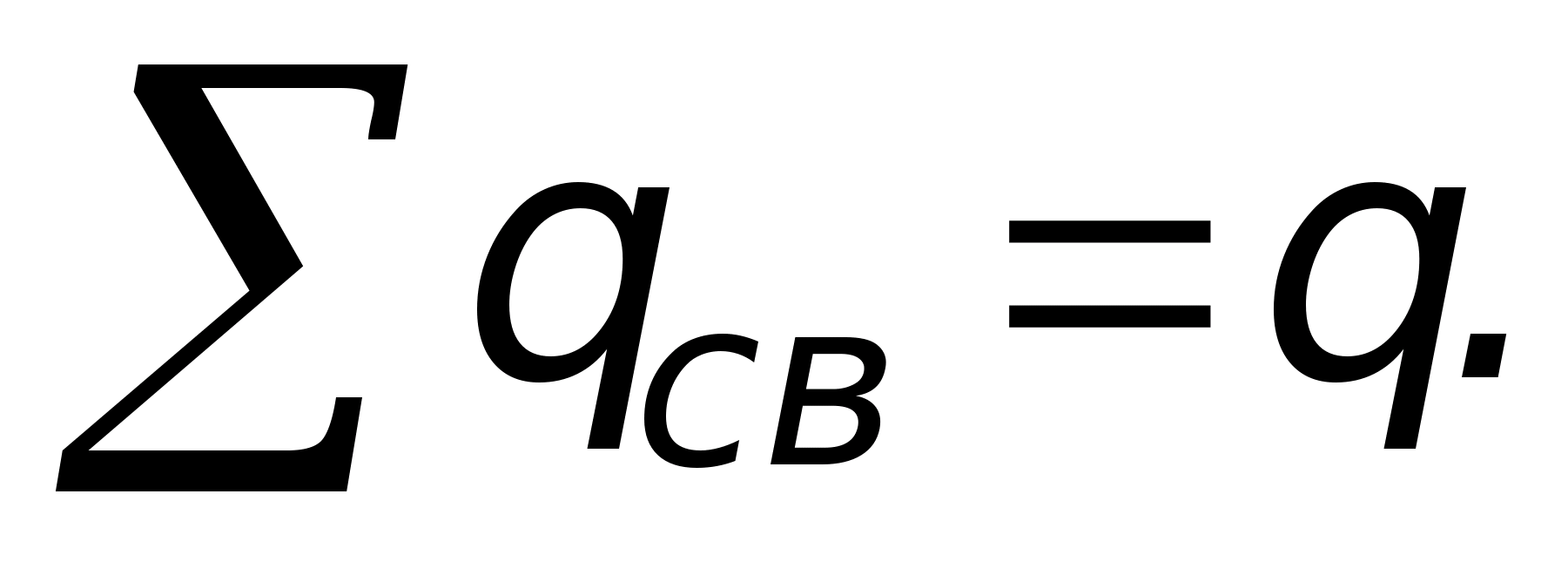 Определим поток вектора
D
через замкнутую поверхность,
охватывающую эту пластину (рис.11.19)
Определим поток вектора
D
через замкнутую поверхность,
охватывающую эту пластину (рис.11.19)
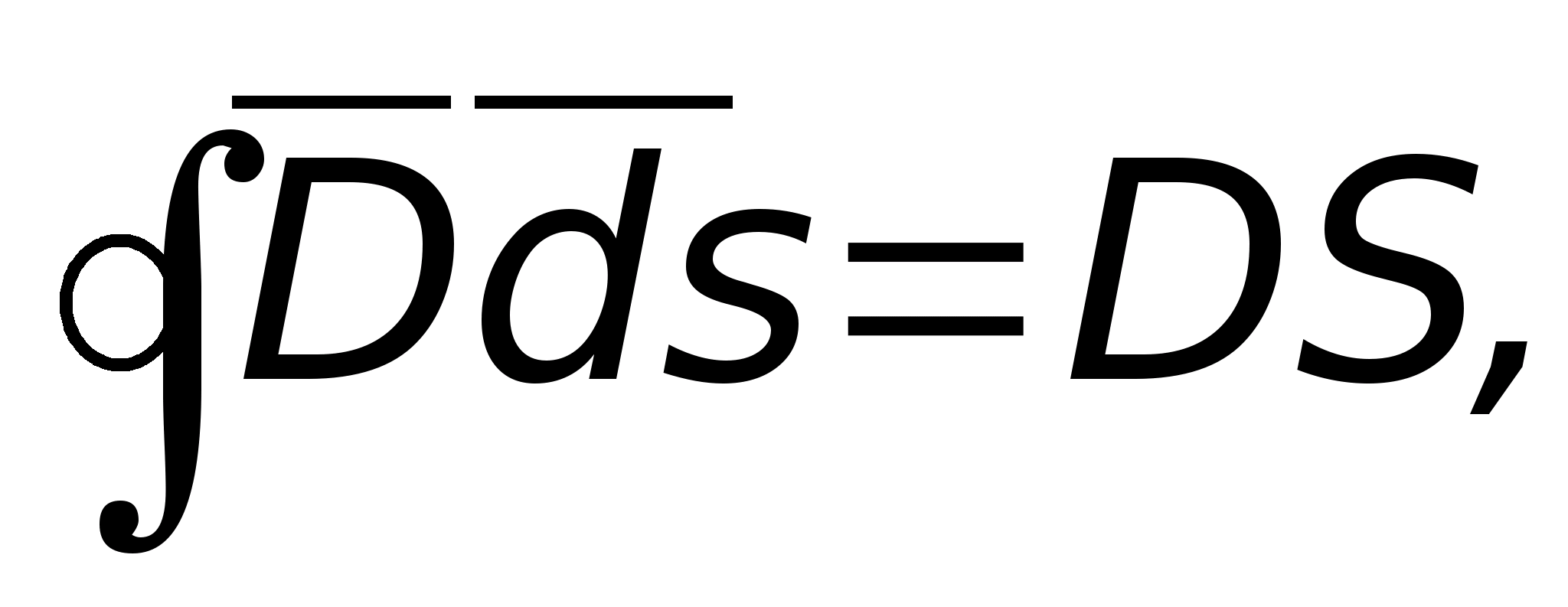 так как векторы D
и ds
совпадают по направлению
и D
имеет одно и тоже значение
во всех точках, находящихся внутри
конденсатора. Следовательно, q=DS=
ε
a
ES
и
так как векторы D
и ds
совпадают по направлению
и D
имеет одно и тоже значение
во всех точках, находящихся внутри
конденсатора. Следовательно, q=DS=
ε
a
ES
и
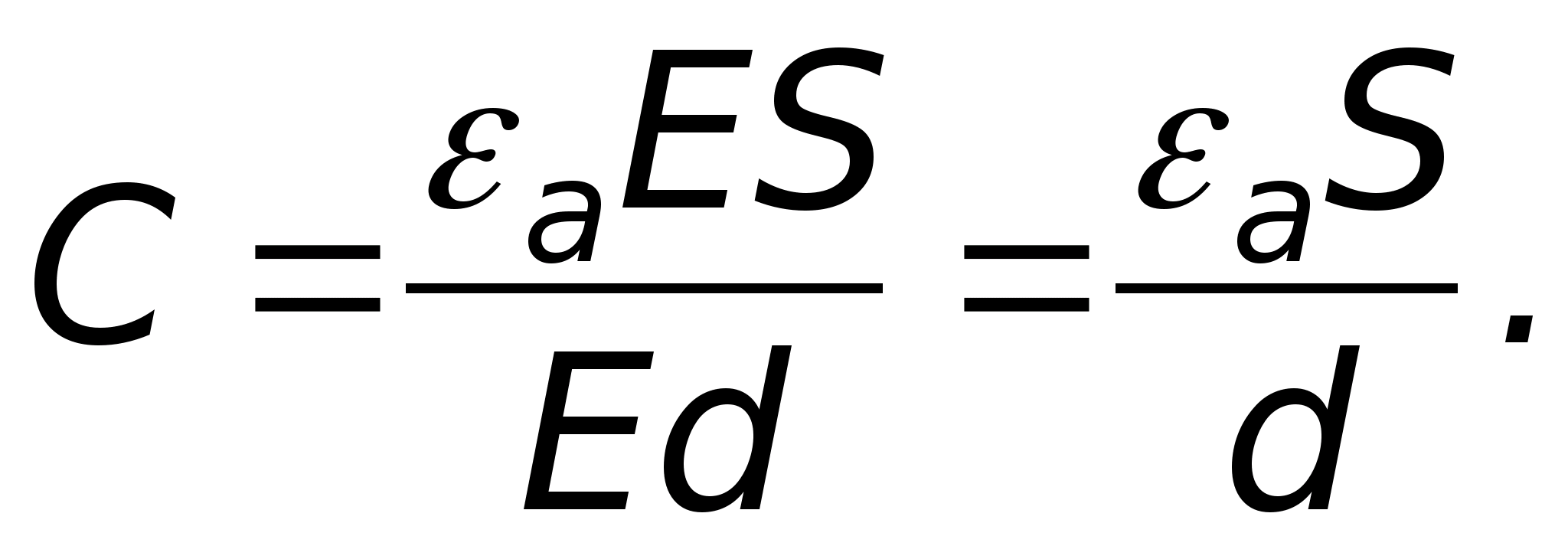
Д вухслойный
конденсатор (рис.11.20) отличается от
предыдущего тем, что изоляция между
пластинами состоит из двух слоёв с
проницаемостями ε 1а
и ε 2а. Если
по-прежнему пренебречь краевым эффектом,
то поле такого конденсатора характерно
тем, что в каждом слое
оно является однородным с напряженностями
Е
1
и Е
2
соответственно. Тогда
вухслойный
конденсатор (рис.11.20) отличается от
предыдущего тем, что изоляция между
пластинами состоит из двух слоёв с
проницаемостями ε 1а
и ε 2а. Если
по-прежнему пренебречь краевым эффектом,
то поле такого конденсатора характерно
тем, что в каждом слое
оно является однородным с напряженностями
Е
1
и Е
2
соответственно. Тогда
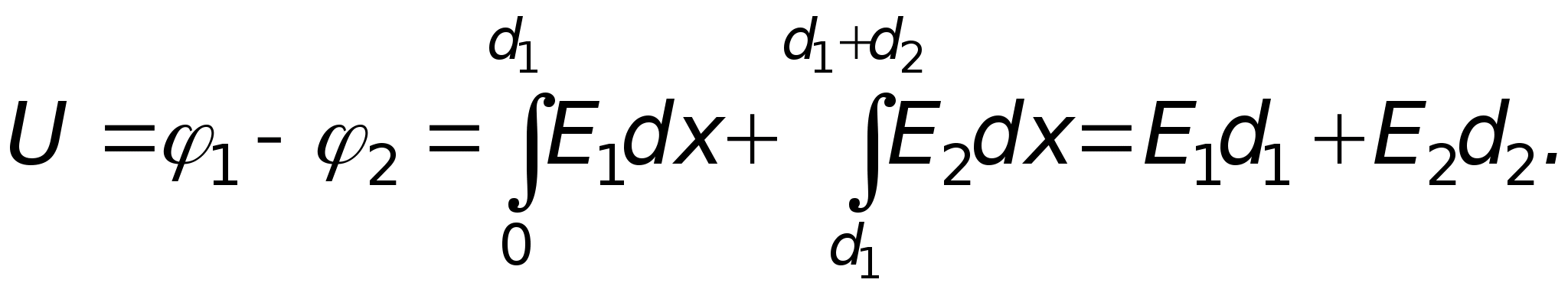 Однако этого уравнения недостаточно
для определения Е
1
и Е
2 .
Для составления второго
уравнения используем граничные условия.
Известно, что на границе раздела двух
разных диэлектриков равны нормальные
составляющие вектора электростатической
индукции (D
1 n
=D
2 n
).
Если учесть, что в нашем
случае эти векторы перпендикулярны к
границе, то это равенство примет вид
D
1 =D
2
или ε
1 а
Е
1 =
ε
2 а
Е
2 .
Это и будет второе уравнение. Решая
совместно эти уравнения, получим
Однако этого уравнения недостаточно
для определения Е
1
и Е
2 .
Для составления второго
уравнения используем граничные условия.
Известно, что на границе раздела двух
разных диэлектриков равны нормальные
составляющие вектора электростатической
индукции (D
1 n
=D
2 n
).
Если учесть, что в нашем
случае эти векторы перпендикулярны к
границе, то это равенство примет вид
D
1 =D
2
или ε
1 а
Е
1 =
ε
2 а
Е
2 .
Это и будет второе уравнение. Решая
совместно эти уравнения, получим
Определим закон изменения потенциала:
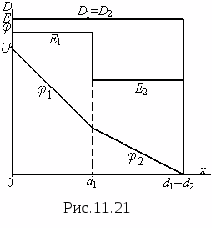
Постоянную интегрирования А 1 определим из условия, что при х =0 φ 1 = U (А 1 =U ), а А 2 – из условия, что при х =d 1 φ 1 =φ 2 (или φ 2 =0 при х =d 1 +d 2). Из полученных формул видно, что потенциал изменяется по линейному закону. На рис.11.21 показаны графики зависимости от х индукций, напряженностей и потенциалов.
Ёмкость такого конденсатора определяется как эквивалентная двух последовательно соединенных ёмкостей:
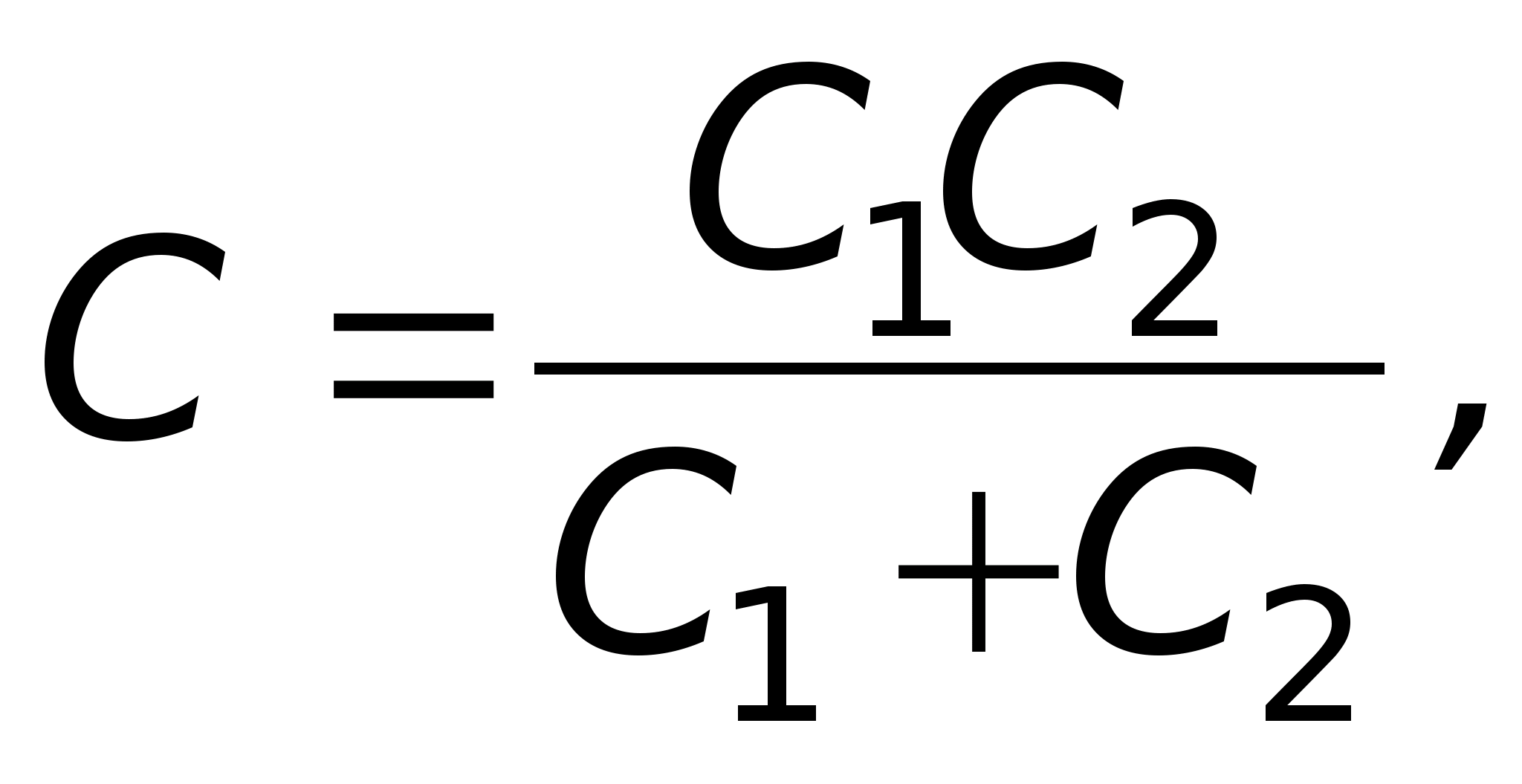 где
где
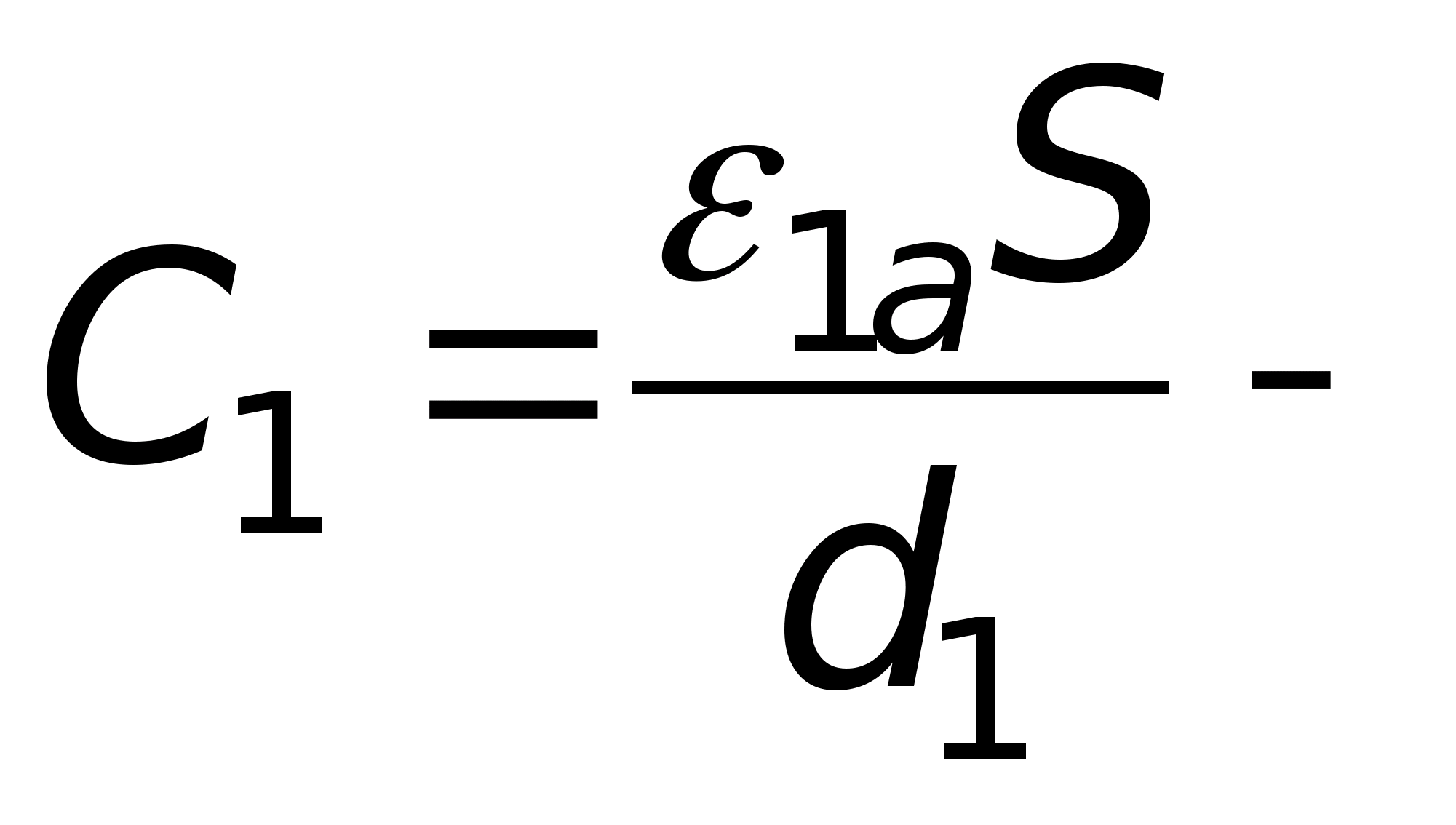 ёмкость первого слоя, а
ёмкость первого слоя, а
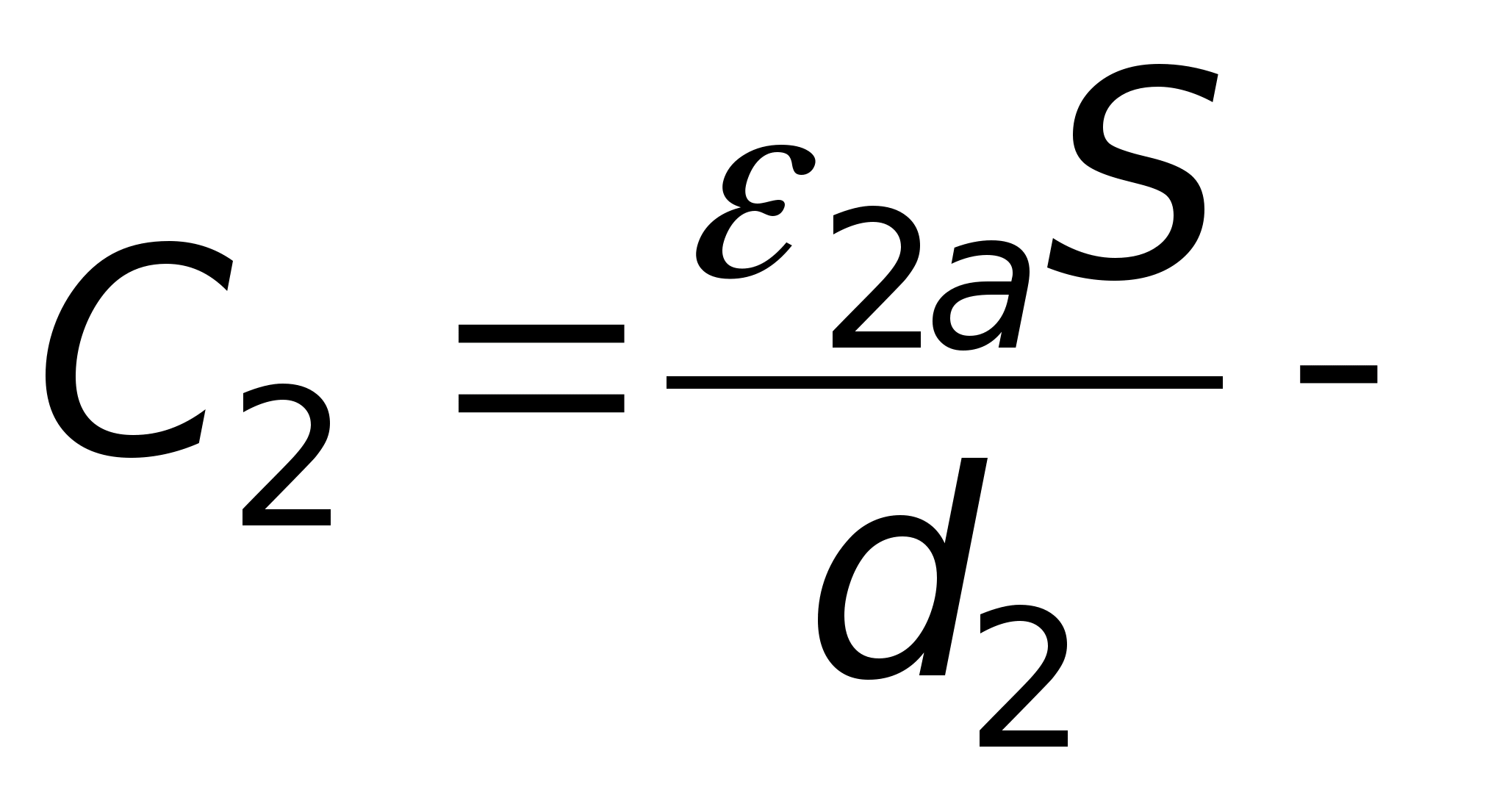 ёмкость второго слоя изоляции
конденсатора.
ёмкость второго слоя изоляции
конденсатора.
Метод зеркальных изображений
Данный метод применяется для расчета полей, в которых имеется геометрически правильной формы граница раздела различных сред. Это искусственный расчетный метод, сущность которого заключается в том, что в расчет кроме заданных зарядов вводятся еще дополнительные или фиктивные заряды, величина и место расположения которых выбираются такими, чтобы выполнялись граничные условия. Чаще всего фиктивные заряды располагаются в точках зеркального изображения по отношению к заданным, отсюда и название метода. Дополнительные или фиктивные заряды в расчет вводятся для того, чтобы учесть влияние появляющихся в результате электростатической индукции свободные или связанные заряды.
Поле заряженной оси, расположенной вблизи проводящей поверхности
П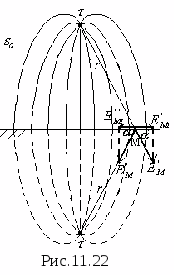 усть
заряженная ось с зарядом
расположена параллельно поверхности
проводящей среды (рис.11.22). Этой проводящей
средой может быть металлическая плита
или стенка дома, но чаще всего это земля.
Вследствие электростатической индукции
на поверхности проводящего тела наводятся
заряды, наличие которых приводит к
искажению поля по сравнению с полем
уединенной оси. Распределение
индуктированных зарядов по поверхности
проводящей среды является весьма сложным
и неизвестным. Несмотря на это задача
расчета поля в верхнем полупространстве,
заполненном диэлектриком с проницаемостью
а
(в нижнем полупространстве поля нет
поскольку там проводящая среда), может
быть достаточно просто решена методом
зеркальных изображений. Поместим в
точку, являющуюся зеркальным изображением
заданной оси относительно проводящей
поверхности, фиктивную ось с зарядом
такой же величины, но противоположного
знака, т.е. -
(заметим, что так будет не всегда,
фиктивный заряд может иметь и другие
величины и знак). Убедимся в том, что
напряженность Е
от двух заряженных осей (
и -
)
в любой точке границы раздела сред не
имеет тангенциальной составляющей.
Действительно,
так как тангенциальные составляющие
от обоих зарядов имеют противоположные
направления и в сумме дают ноль.
Следовательно, граничные условия между
диэлектриком и проводником выполняются,
что доказывает правильность выбора
величины и места расположения фиктивного
заряда. Поэтому напряженность поля и
потенциал в любой точке диэлектрика
можно определять по известным формулам
поля двух заряженных осей:
где а
– расстояние до положительно заряженной
оси, b
– расстояние до отрицательно
заряженной оси. Если бы фактическая ось
несла на себе заряд -
,
то задача решалась бы аналогично, только
фиктивная ось имела бы заряд +
.
Аналогично решается задача о поле
точечного заряда, расположенного вблизи
проводящей среды.
усть
заряженная ось с зарядом
расположена параллельно поверхности
проводящей среды (рис.11.22). Этой проводящей
средой может быть металлическая плита
или стенка дома, но чаще всего это земля.
Вследствие электростатической индукции
на поверхности проводящего тела наводятся
заряды, наличие которых приводит к
искажению поля по сравнению с полем
уединенной оси. Распределение
индуктированных зарядов по поверхности
проводящей среды является весьма сложным
и неизвестным. Несмотря на это задача
расчета поля в верхнем полупространстве,
заполненном диэлектриком с проницаемостью
а
(в нижнем полупространстве поля нет
поскольку там проводящая среда), может
быть достаточно просто решена методом
зеркальных изображений. Поместим в
точку, являющуюся зеркальным изображением
заданной оси относительно проводящей
поверхности, фиктивную ось с зарядом
такой же величины, но противоположного
знака, т.е. -
(заметим, что так будет не всегда,
фиктивный заряд может иметь и другие
величины и знак). Убедимся в том, что
напряженность Е
от двух заряженных осей (
и -
)
в любой точке границы раздела сред не
имеет тангенциальной составляющей.
Действительно,
так как тангенциальные составляющие
от обоих зарядов имеют противоположные
направления и в сумме дают ноль.
Следовательно, граничные условия между
диэлектриком и проводником выполняются,
что доказывает правильность выбора
величины и места расположения фиктивного
заряда. Поэтому напряженность поля и
потенциал в любой точке диэлектрика
можно определять по известным формулам
поля двух заряженных осей:
где а
– расстояние до положительно заряженной
оси, b
– расстояние до отрицательно
заряженной оси. Если бы фактическая ось
несла на себе заряд -
,
то задача решалась бы аналогично, только
фиктивная ось имела бы заряд +
.
Аналогично решается задача о поле
точечного заряда, расположенного вблизи
проводящей среды.
Электростатическое поле системы проводников, расположенных вблизи проводящей поверхности (частичные ёмкости)
В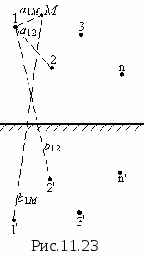 качестве системы проводников, расположенных
вблизи проводящей поверхности, рассмотрим
многопроводную линию электропередачи
(ЛЭП), состоящую из n
весьма длинных проводов, протянутых
параллельно поверхности земли (рис.11.23).
качестве системы проводников, расположенных
вблизи проводящей поверхности, рассмотрим
многопроводную линию электропередачи
(ЛЭП), состоящую из n
весьма длинных проводов, протянутых
параллельно поверхности земли (рис.11.23).
Пусть известны заряды каждого провода к (будем считать их положительными), их радиусы r к, высоты подвеса h к, взаимное расположение и свойства среды ( а ), в которой они находятся. Вследствие электростатической индукции на поверхности земли появятся свободные заряды, которые окажут влияние на результирующее электростатическое поле. Для учета этого влияния воспользуемся методом зеркальных изображений, для чего введём в расчет n фиктивных проводов, расположенных в точках зеркального изображения по отношению к заданным. Возьмём в диэлектрике произвольную точку М и определим её потенциал, используя метод наложения: М = М 1 ` + М 2 + М 3 +…+ М n , где М 1 – составляющая потенциала, создаваемая первым проводом и его зеркальным изображением, М 2 - составляющая, создаваемая вторым проводом и его зеркальным изображением и т.д. Будем полагать, что высоты подвеса проводов намного больше их радиусов, и тогда можно считать, что электрические и геометрические оси проводов совпадают. С учетом сказанного можно записать:
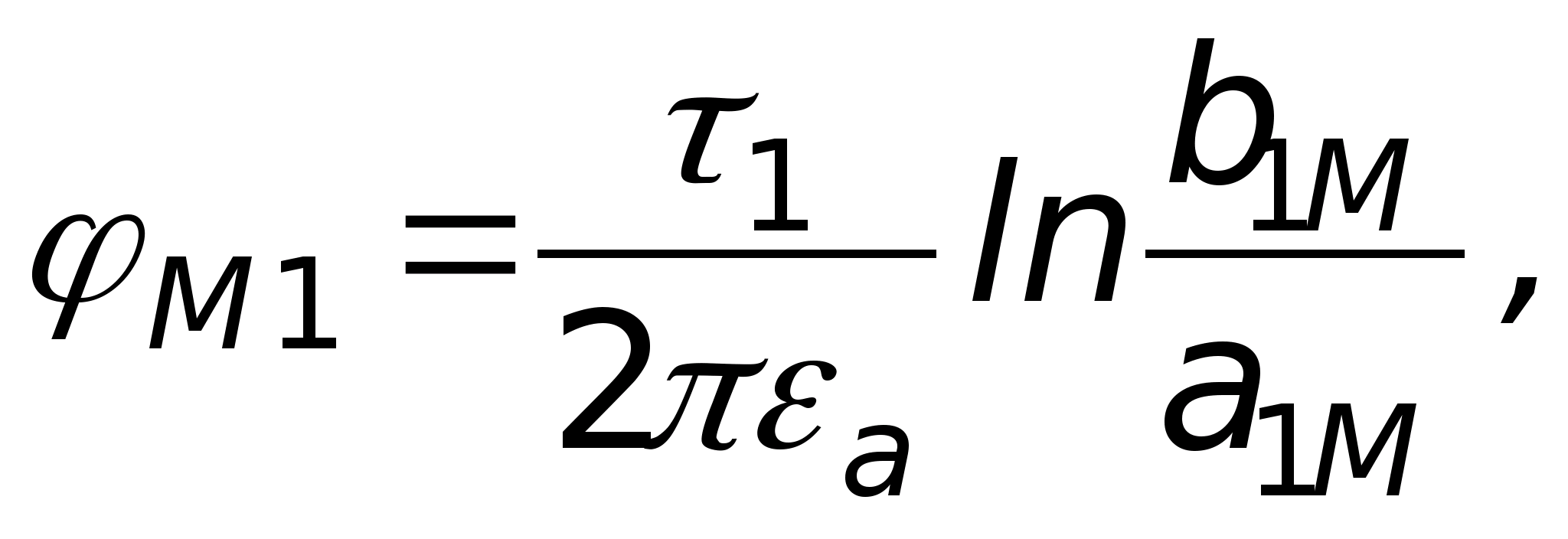 где а
1 М
- расстояние от
точки М
до оси первого провода;
b
1 M
– расстояние от точки М
до зеркального изображения первого
провода;
где а
1 М
- расстояние от
точки М
до оси первого провода;
b
1 M
– расстояние от точки М
до зеркального изображения первого
провода;
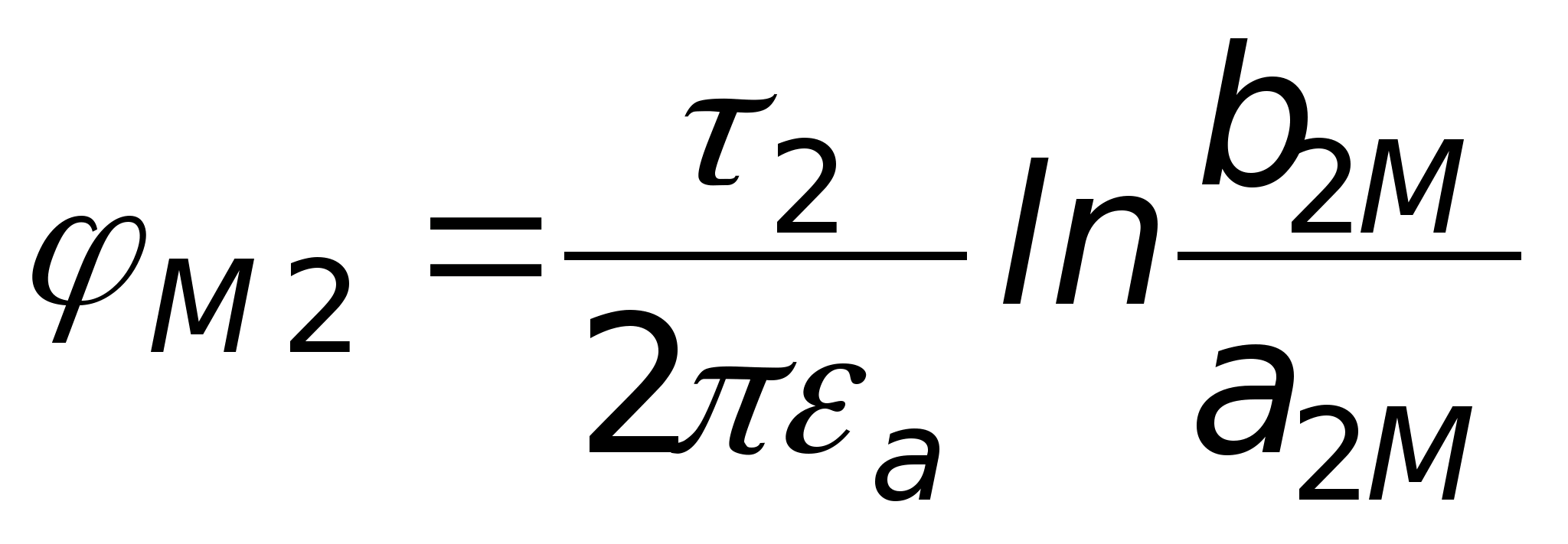 и т.д. Тогда
и т.д. Тогда
Если точку М поместить на поверхность первого провода, то его потенциал можно определить по этой формуле, если учесть, что а 1 М =r 1 , b 1 M =2h 1 , а 2 М =а 12 – расстояние между первым и вторым проводниками, b 2 M = b 12 - расстояние от первого проводника до зеркального изображения второго и т.д., то получим
Аналогично можно определить потенциалы всех проводов ЛЭП и если это сделать, то получим первую группу формул Максвелла:
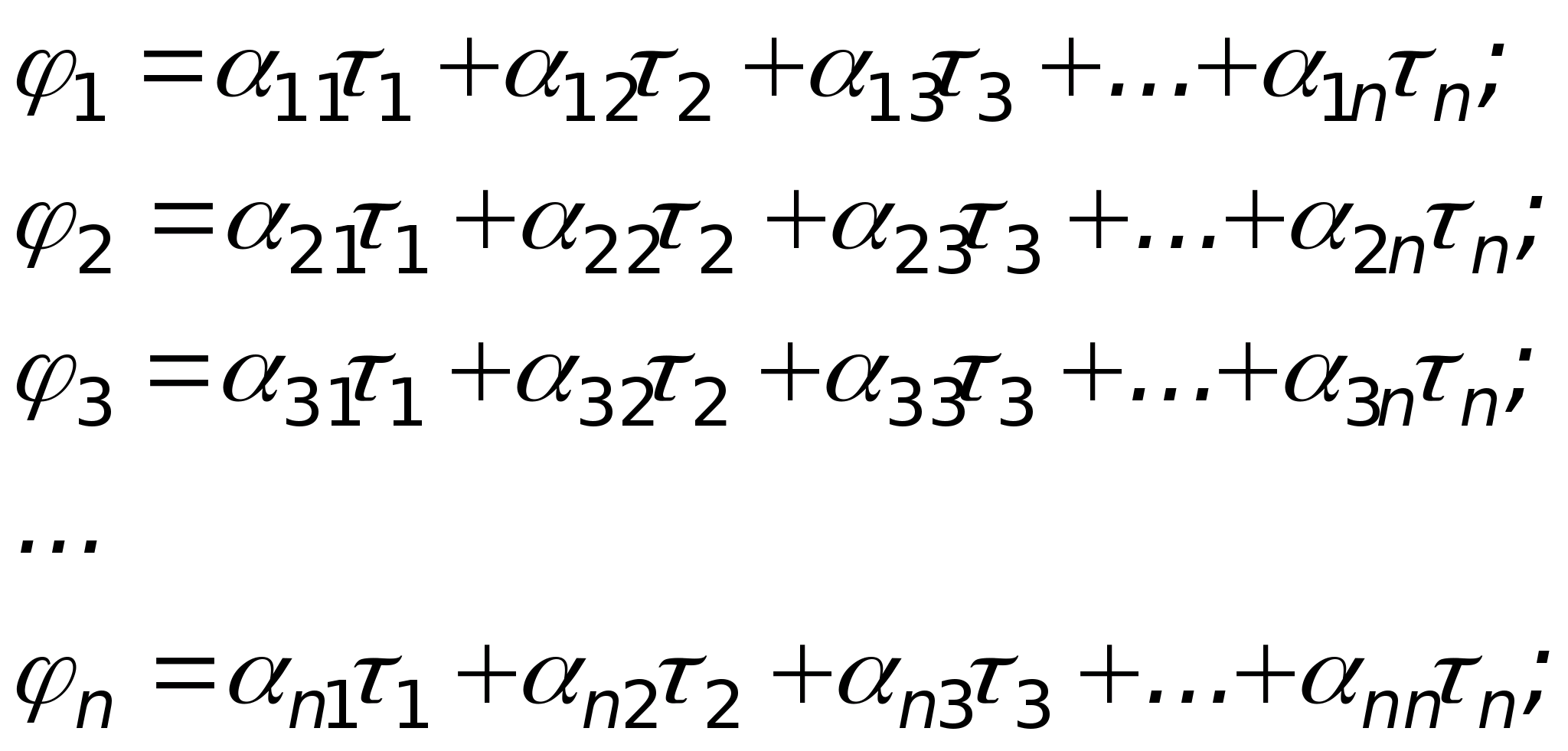
В этих уравнениях Коэффициенты кк и к m зависят только от геометрических размеров тел, их взаимного расположения и от свойств среды, в которой они находятся. Называются они потенциальными коэффициентами, измеряются в м/Ф и все являются положительными (под знаком логарифма стоит дробь, числитель которой всегда больше знаменателя). Им можно дать такое толкование. Пусть заряды всех проводов кроме первого равны нулю, а 1 =1. Тогда первая группа формул Максвелла принимает вид: 1 = 11 ; 2 = 21 ; 3 = 31 ; … n = n 1 . Следовательно, 11 равен потенциалу первого провода, если на нём заряд равен 1, а остальные провода заряда не имеют, 21 равен потенциалу второго провода в указанных условиях и т.д.
Первая группа формул Максвелла определяет потенциалы проводов по их зарядам. Однако на практике часто возникает обратная задача определения зарядов проводов по их потенциалам. Это можно сделать, если первую группу формул Максвелла решить относительно зарядов, полагая потенциалы проводов и коэффициенты известными. Тогда получим вторую группу формул Максвелла:
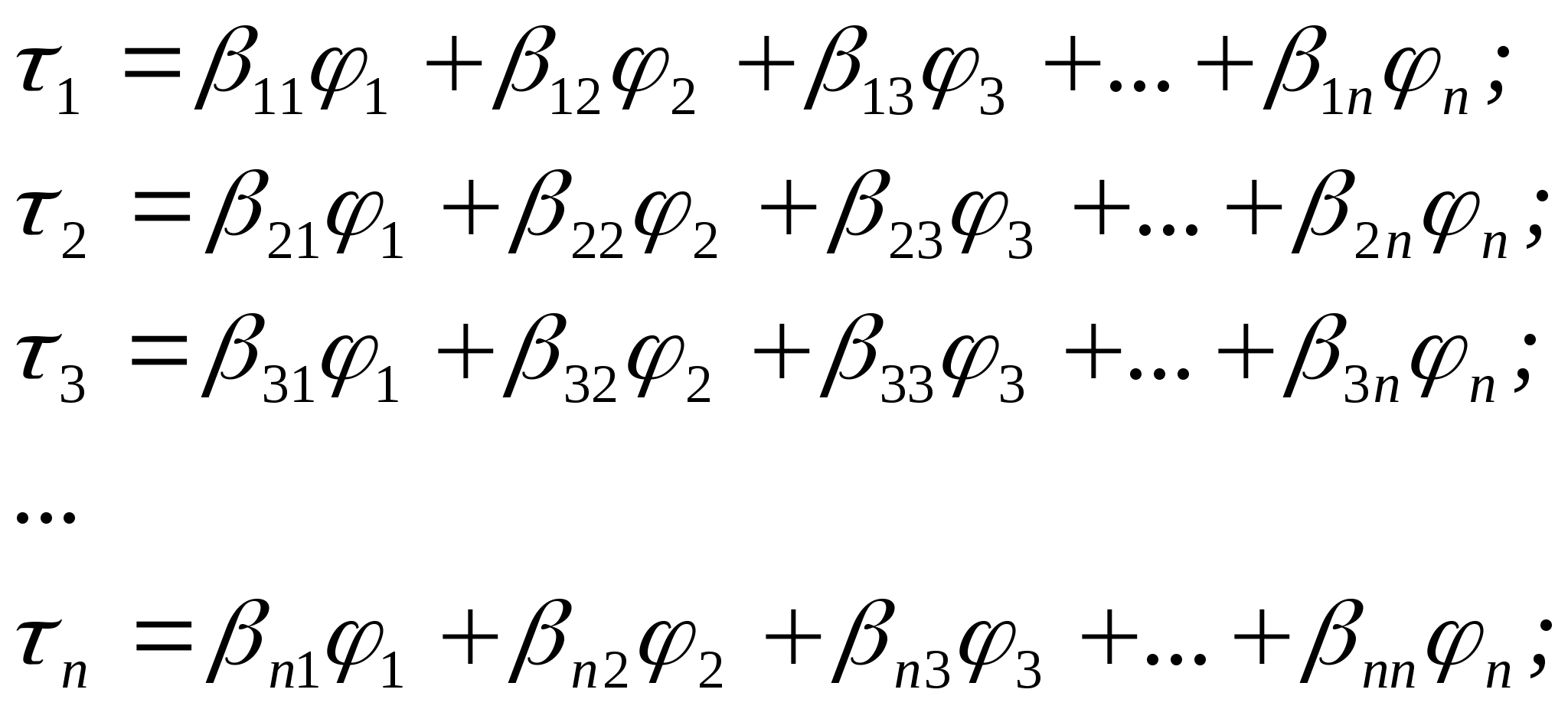
з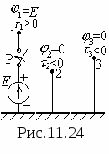 десь
десь
![]() где
- главный определитель первой группы
формул Максвелла, состоящий из
потенциальных коэффициентов
,
а к m –
алгебраическое дополнение, получаемое
из
путём вычеркивания к
-ой
строки, m
-го
столбца и умножения оставшегося
определителя на
где
- главный определитель первой группы
формул Максвелла, состоящий из
потенциальных коэффициентов
,
а к m –
алгебраическое дополнение, получаемое
из
путём вычеркивания к
-ой
строки, m
-го
столбца и умножения оставшегося
определителя на
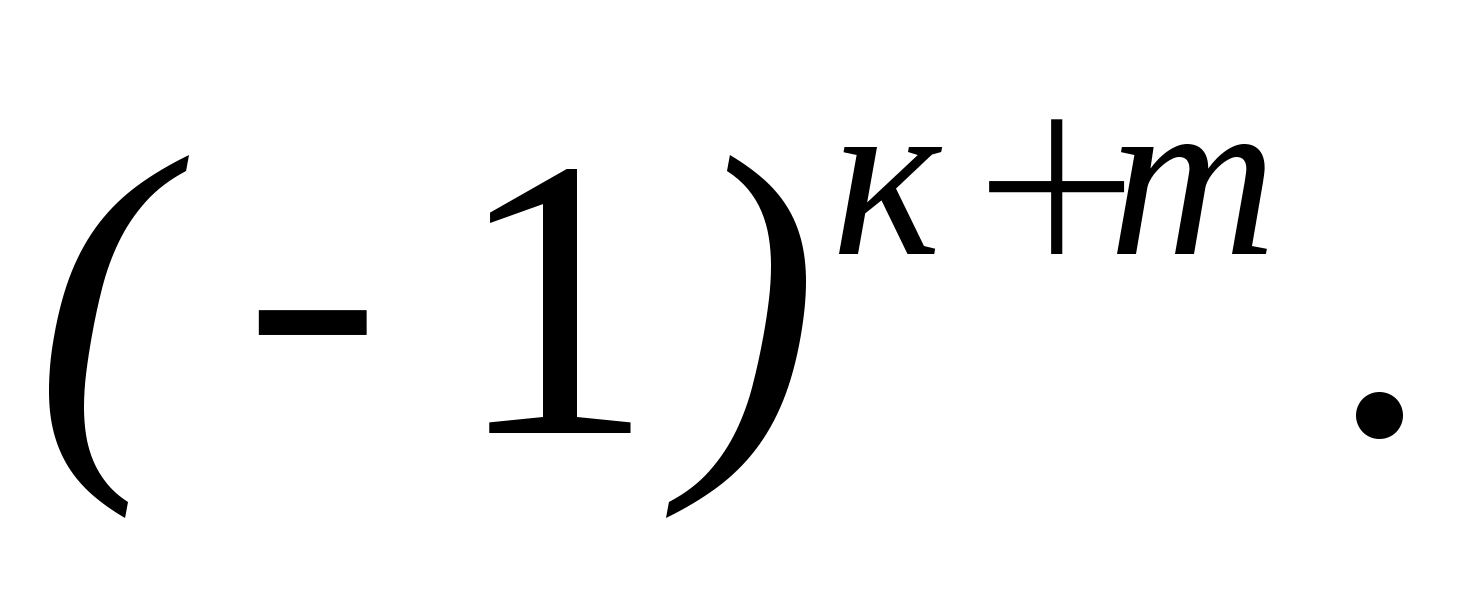 Размерность емкостных коэффициентов
обратна размерности потенциальных
коэффициентов, т.е. Ф/м
,
поскольку km
на порядок ниже
главного определителя .
Ёмкостные коэффициенты имеют различные
знаки, а именно
кк
>0,
а
к
m( к
m)
1 =Е
,
соединив его с землёй, например, через
источник постоянной ЭДС (рис.11.24). Тогда
на первом проводе накопится некоторый
положительный заряд
1 ,
а точно такой же отрицательный заряд
растечется по всей земле и телам,
соединенным с ней. Части отрицательного
заряда попадут на второй и третий
проводники. Если вторую группу формул
Максвелла переписать для этого опыта,
то получим:
1 =
11
1 ;
2 =
21
1 ;
3 =
3 1
1 ,
Размерность емкостных коэффициентов
обратна размерности потенциальных
коэффициентов, т.е. Ф/м
,
поскольку km
на порядок ниже
главного определителя .
Ёмкостные коэффициенты имеют различные
знаки, а именно
кк
>0,
а
к
m( к
m)
1 =Е
,
соединив его с землёй, например, через
источник постоянной ЭДС (рис.11.24). Тогда
на первом проводе накопится некоторый
положительный заряд
1 ,
а точно такой же отрицательный заряд
растечется по всей земле и телам,
соединенным с ней. Части отрицательного
заряда попадут на второй и третий
проводники. Если вторую группу формул
Максвелла переписать для этого опыта,
то получим:
1 =
11
1 ;
2 =
21
1 ;
3 =
3 1
1 ,
о ткуда
имеем:
Ёмкостные коэффициенты
можно определять экспериментальным
путём. Если после зарядки системы,
включить гальванометры G 1 -G 3
(рис.11.25) и замкнуть ключ, то
система разрядится и в процессе разряда
гальванометры измерят заряды
1 -
3
соответственно. Тогда
по последним формулам, зная
1 ,
можно определить
11 -
31 .
Следует заметить,
к
m
=
mк
,
поскольку к
m
= mк
из-за
симметричности
относительно главной диагонали.
ткуда
имеем:
Ёмкостные коэффициенты
можно определять экспериментальным
путём. Если после зарядки системы,
включить гальванометры G 1 -G 3
(рис.11.25) и замкнуть ключ, то
система разрядится и в процессе разряда
гальванометры измерят заряды
1 -
3
соответственно. Тогда
по последним формулам, зная
1 ,
можно определить
11 -
31 .
Следует заметить,
к
m
=
mк
,
поскольку к
m
= mк
из-за
симметричности
относительно главной диагонали.
Вторая группа формул Максвелла неудобна в том отношении, что в ней фигурируют потенциалы проводов, а не напряжения между ними. Поэтому часто эту систему переписывают так, чтобы в правой части фигурировали напряжения между рассматриваемым проводником и всеми остальными, в том числе и землёй.
Любая строка второй группы формул Максвелла может быть записана в компактной форме
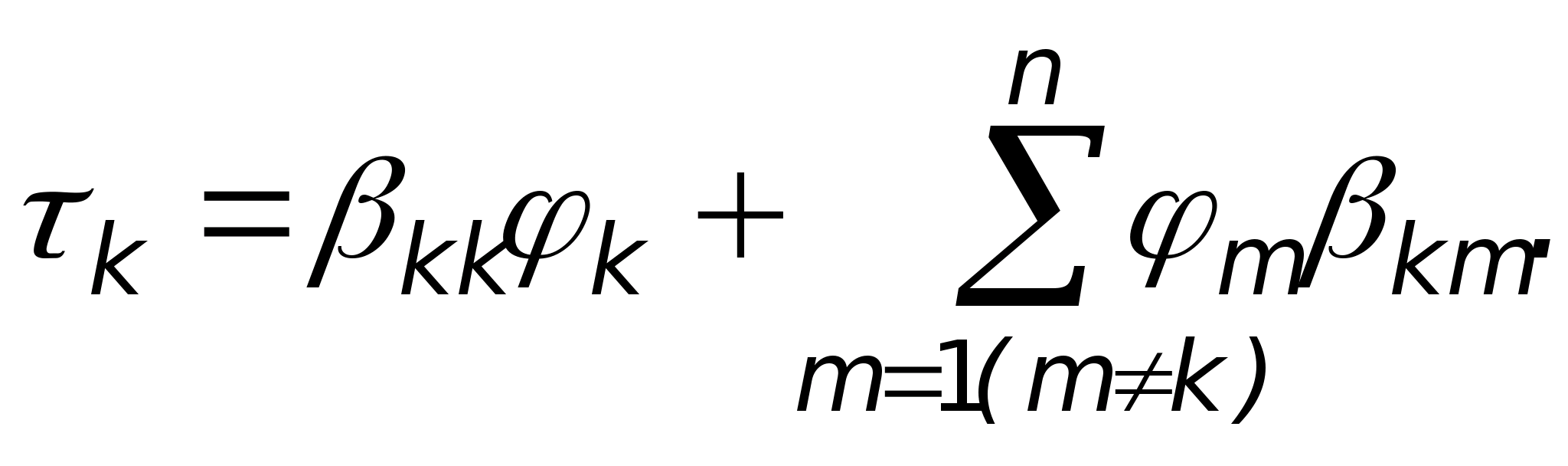 Преобразуем выражение
Преобразуем выражение
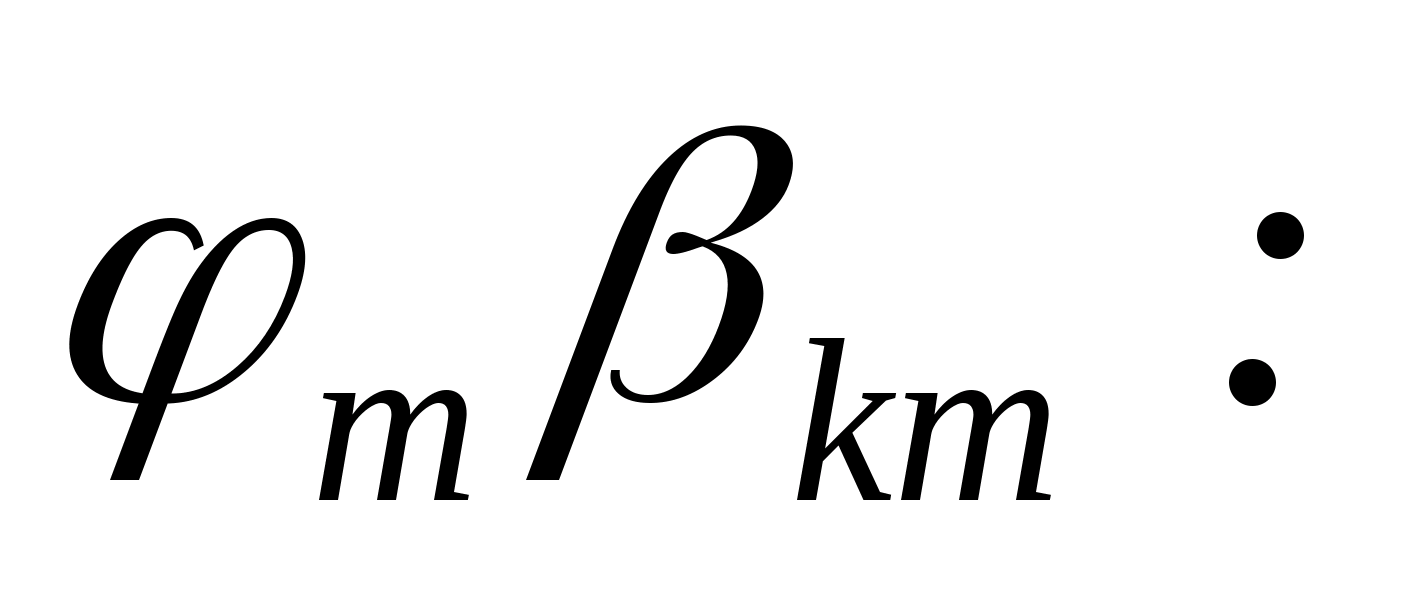 где
где
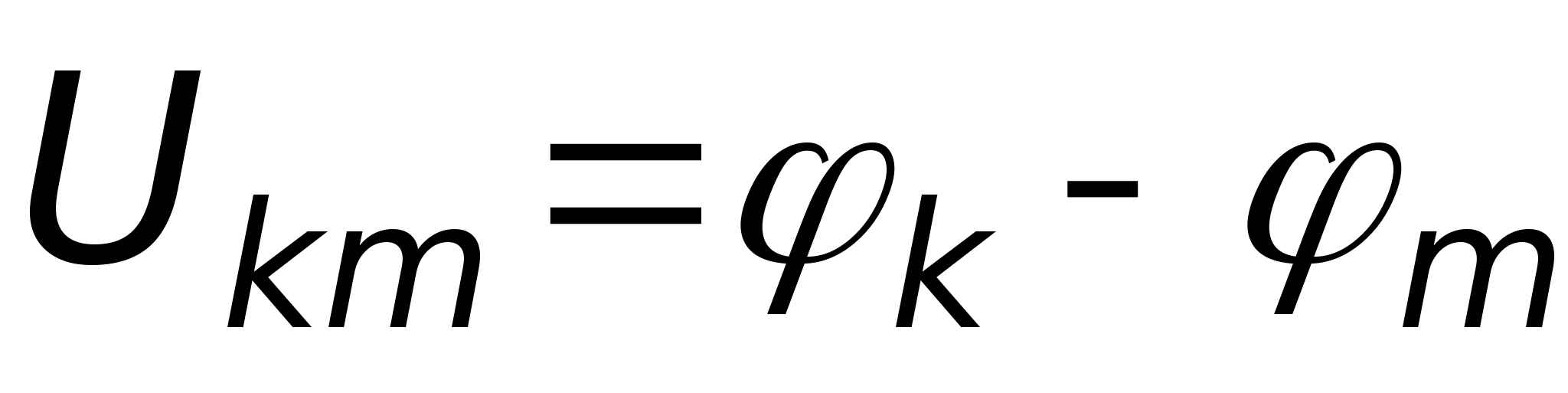 - напряжение между к
-м
и m
-м
проводами. Тогда
Обозначив
- напряжение между к
-м
и m
-м
проводами. Тогда
Обозначив
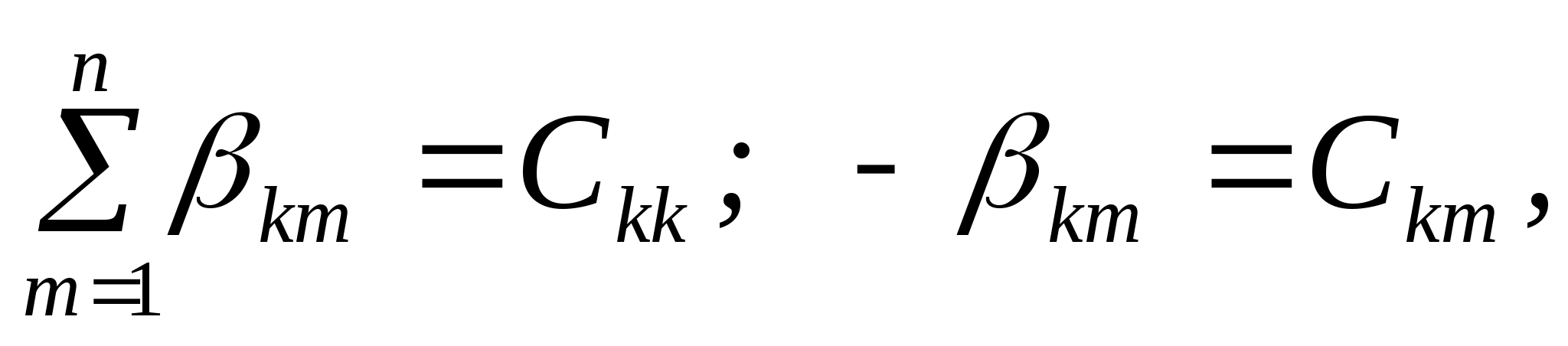 получим
получим
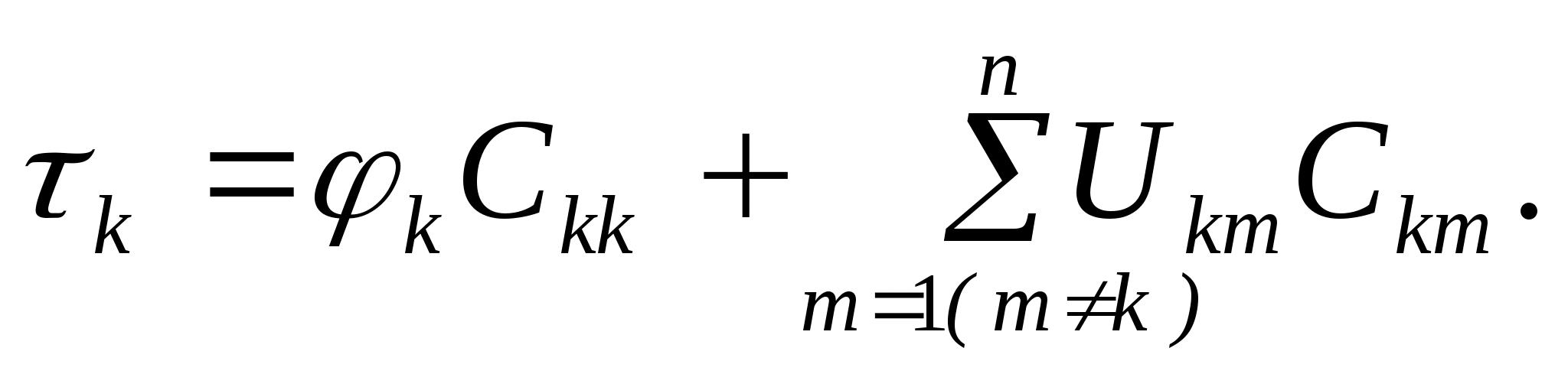 Придавая индексу k
значения от 1 до n
,
распишем систему уравнений, которая
получила название третей группы
формул Максвелла:
Придавая индексу k
значения от 1 до n
,
распишем систему уравнений, которая
получила название третей группы
формул Максвелла:
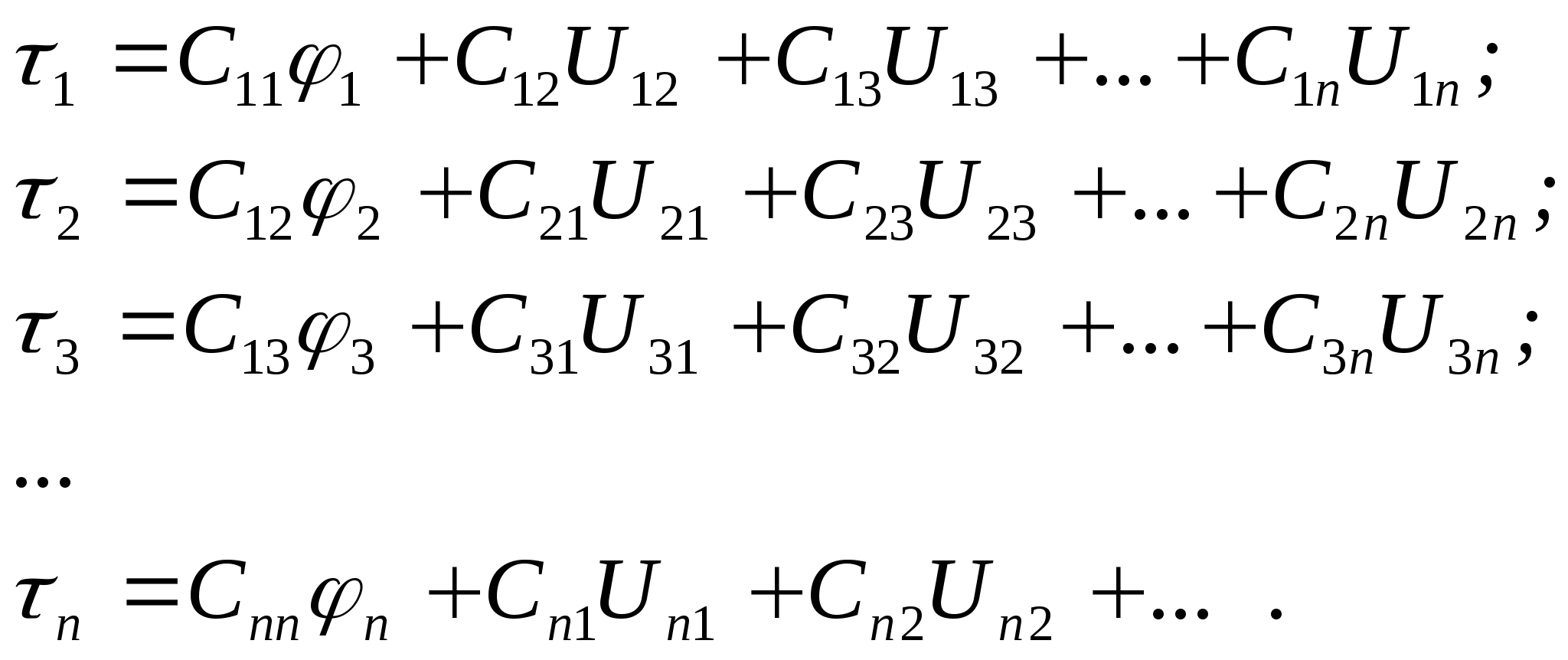
В ходящие
в эти уравнения коэффициенты С
получили название частичных ёмкостей,
причем
называется
собственной частичной ёмкостью k
-го
проводника. В указанной сумме положительным
является только одно слагаемое (
kk
),
тем не менее С
kk
всегда положительна. В этом можно
убедиться, проделав следующий опыт:
соединим (тоненькими проводочками) все
провода ЛЭП с первым и произведём
зарядку этой системы, соединив её с
землёй через источник постоянной ЭДС
(рис.11.26). Тогда на первом проводе накопится
некоторый положительный заряд
1 ,
а его потенциал
1 =Е
>0.
Первое уравнение третей
группы формул Максвелла для этого опыта
имеет вид (U
12 =0,
U
13 =0)
1 =C
11
1 ,
откуда имеем
ходящие
в эти уравнения коэффициенты С
получили название частичных ёмкостей,
причем
называется
собственной частичной ёмкостью k
-го
проводника. В указанной сумме положительным
является только одно слагаемое (
kk
),
тем не менее С
kk
всегда положительна. В этом можно
убедиться, проделав следующий опыт:
соединим (тоненькими проводочками) все
провода ЛЭП с первым и произведём
зарядку этой системы, соединив её с
землёй через источник постоянной ЭДС
(рис.11.26). Тогда на первом проводе накопится
некоторый положительный заряд
1 ,
а его потенциал
1 =Е
>0.
Первое уравнение третей
группы формул Максвелла для этого опыта
имеет вид (U
12 =0,
U
13 =0)
1 =C
11
1 ,
откуда имеем
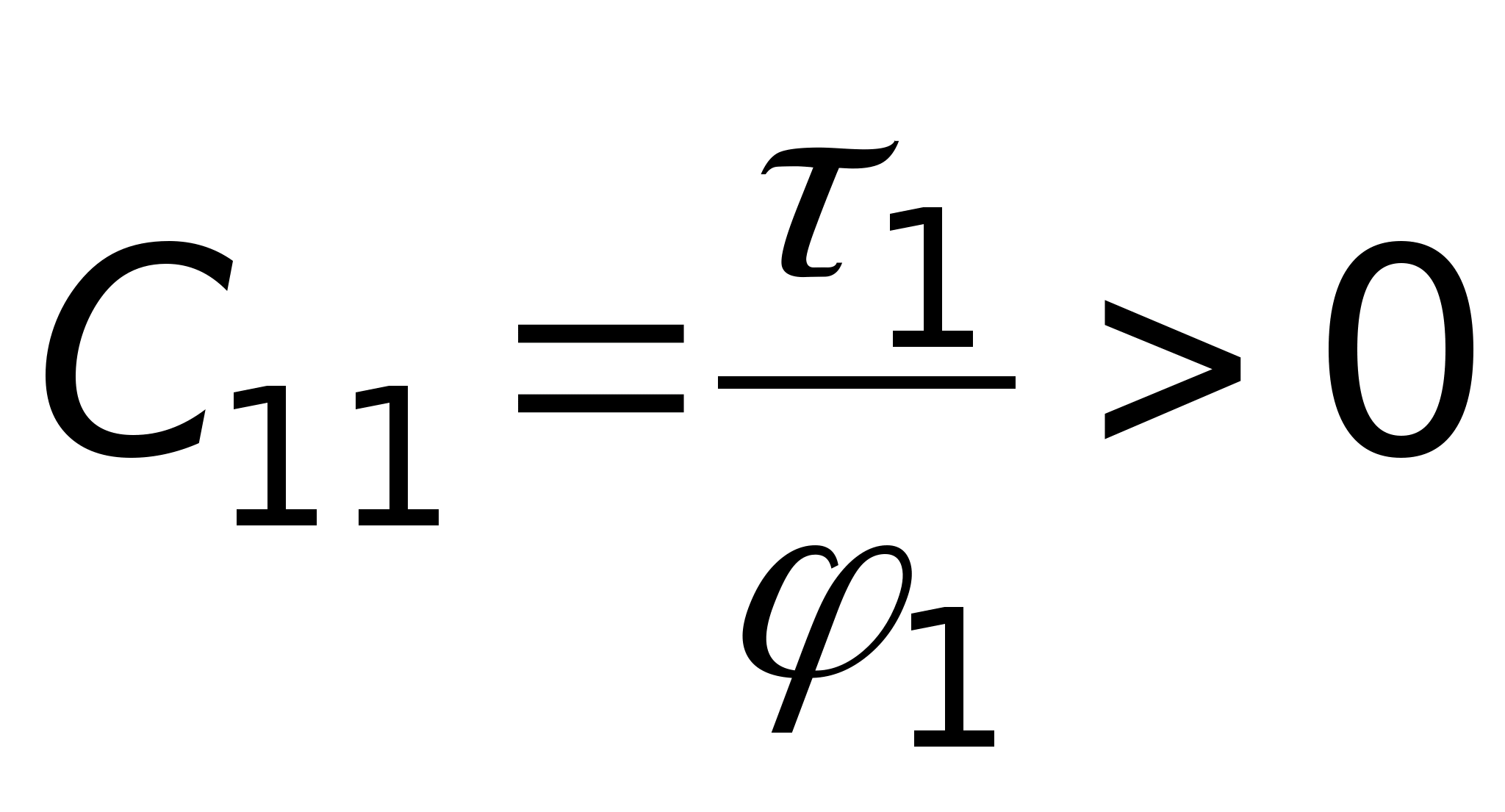 .
.
Собственные частичные ёмкости можно определять экспериментальным путём. Для этого достаточно после зарядки системы измерить 1 и по последней формуле вычислить С 11 . C km =- km называется взаимной частичной ёмкостью k -го и m -го проводников, она также является положительной, поскольку km C km определяется также как km .
Д
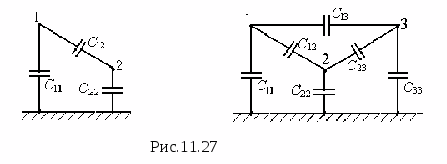 ля
наглядной иллюстрации частичных ёмкостей
приведем два примера. Это будут
совокупности частичных ёмкостей
двухпроводной линии и трёхпроводной
ЛЭП (рис.11.27). Исходя из этих совокупностей
могут быть определены рабочие ёмкости
линий. Так для двухпроводной ЛЭП
ля
наглядной иллюстрации частичных ёмкостей
приведем два примера. Это будут
совокупности частичных ёмкостей
двухпроводной линии и трёхпроводной
ЛЭП (рис.11.27). Исходя из этих совокупностей
могут быть определены рабочие ёмкости
линий. Так для двухпроводной ЛЭП
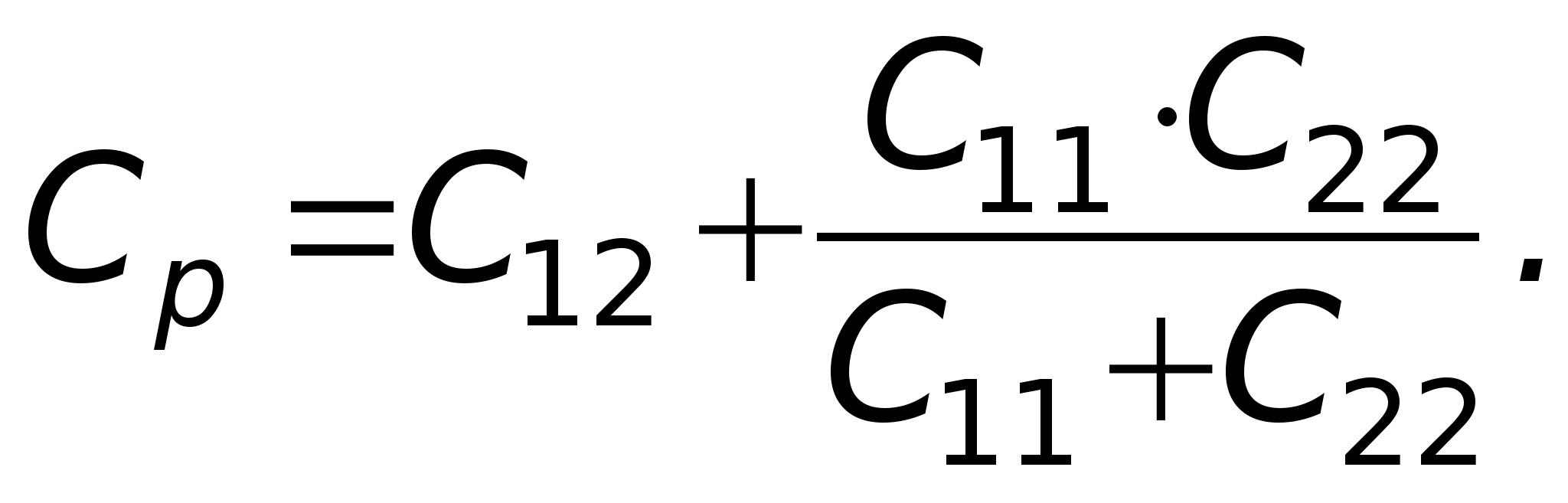
Частичные ёмкости рассчитываются не только для электростатических полей, но используются и при расчете быстропротекающих процессов (например, в электронных лампах и транзисторах – это ёмкости между их электродами), а также при расчете устройств, в основу работы которых положено использование частичных ёмкостей (например, при ёмкостном отборе мощности от высоковольтной ЛЭП).
Третья группа формул Максвелла для системы заряженных тел любой формы. Однако приведенные выше формулы определения потенциальных коэффициентов справедливы только для ЛЭП. Если тела имеют другую форму, то и формулы будут иными. В случае, когда тела имеют сложную форму не удается вывести формулы для коэффициентов и тогда ёмкостные коэффициенты определяют опытным путём.
Электрическое поле постоянного тока в проводящей среде
Проводящей
называется среда, содержащая свободные
заряды. Если в такой среде создать
электрическое поле с напряженностью
Е
,
то на каждый из свободных зарядов q
будет
действовать сила
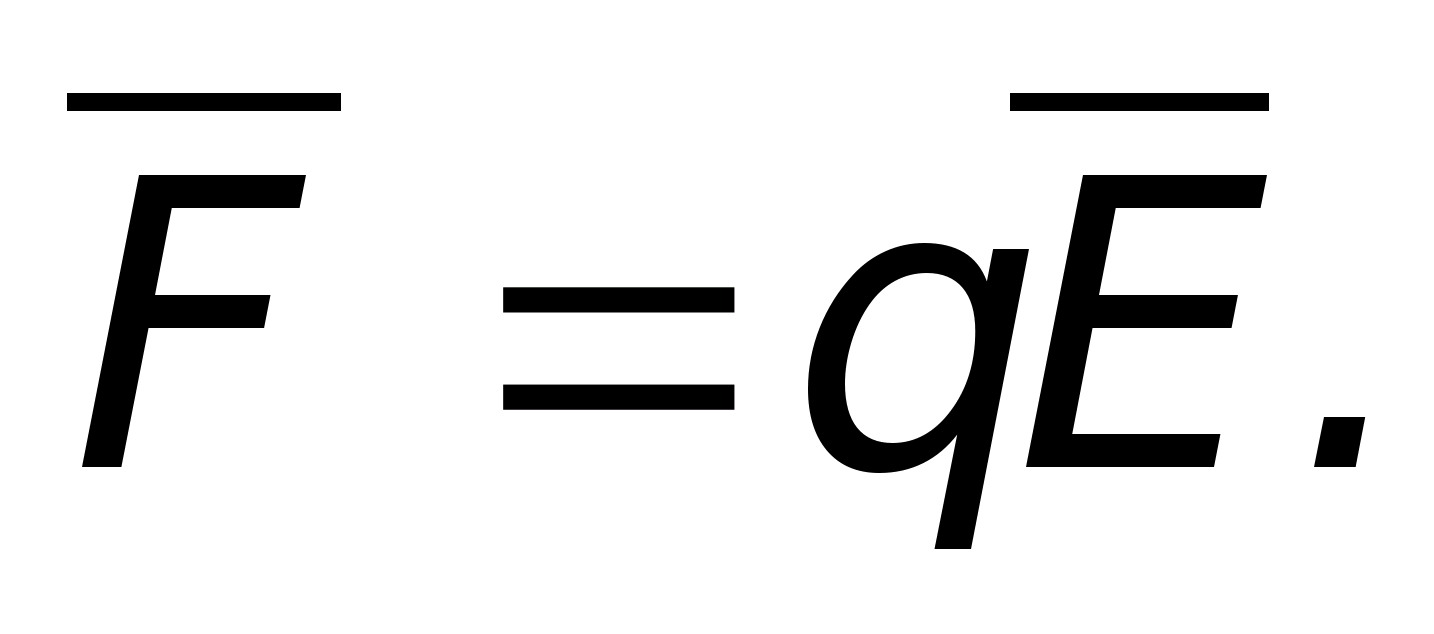 Под
действием этой силы свободные заряды
начнут двигаться, причем упорядоченно.
Упорядоченное же движение частиц,
несущих на себе заряды, есть ток. Таким
образом, в проводящей среде возникает
ток, если в ней создано электрическое
поле. Существует правда несколько видов
тока и ток, протекающий по проводящей
среде принято называть током проводимости.
Следует упомянуть, что свободными
зарядами являются электроны в металлах
и ионы в жидкостях и газах. В процессе
перемещения свободные заряды испытывают
многочисленные столкновения с другими
частицами тела, находящимися в тепловом
движении. Эти столкновения затрудняют
упорядоченное движение носителей
зарядов и являются причиной сопротивления,
оказываемого средой протеканию тока.
Если бы этих столкновений не было, то
не было бы и сопротивления, что имеет
место в сверхпроводниках. Свойство
среды, определяющее её способность
проводить электрический ток характеризуется
удельной проводимостью
.
Она зависит от физических свойств
проводящего материала и от температуры,
а измеряется в См/м
=1/Ом
*
м
.
Под
действием этой силы свободные заряды
начнут двигаться, причем упорядоченно.
Упорядоченное же движение частиц,
несущих на себе заряды, есть ток. Таким
образом, в проводящей среде возникает
ток, если в ней создано электрическое
поле. Существует правда несколько видов
тока и ток, протекающий по проводящей
среде принято называть током проводимости.
Следует упомянуть, что свободными
зарядами являются электроны в металлах
и ионы в жидкостях и газах. В процессе
перемещения свободные заряды испытывают
многочисленные столкновения с другими
частицами тела, находящимися в тепловом
движении. Эти столкновения затрудняют
упорядоченное движение носителей
зарядов и являются причиной сопротивления,
оказываемого средой протеканию тока.
Если бы этих столкновений не было, то
не было бы и сопротивления, что имеет
место в сверхпроводниках. Свойство
среды, определяющее её способность
проводить электрический ток характеризуется
удельной проводимостью
.
Она зависит от физических свойств
проводящего материала и от температуры,
а измеряется в См/м
=1/Ом
*
м
.
Основной
величиной, характеризующей электрическое
поле в проводящей среде (далее -поле в
проводящей среде), является вектор
плотности тока
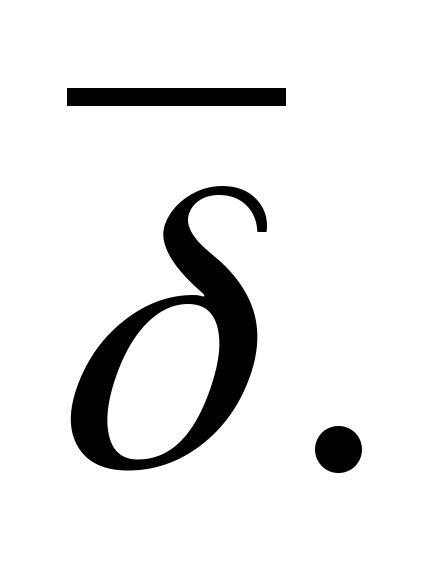 Его направление такое же как и вектора
Е
(понятно из физики явлений), величина
определяется как
Его направление такое же как и вектора
Е
(понятно из физики явлений), величина
определяется как
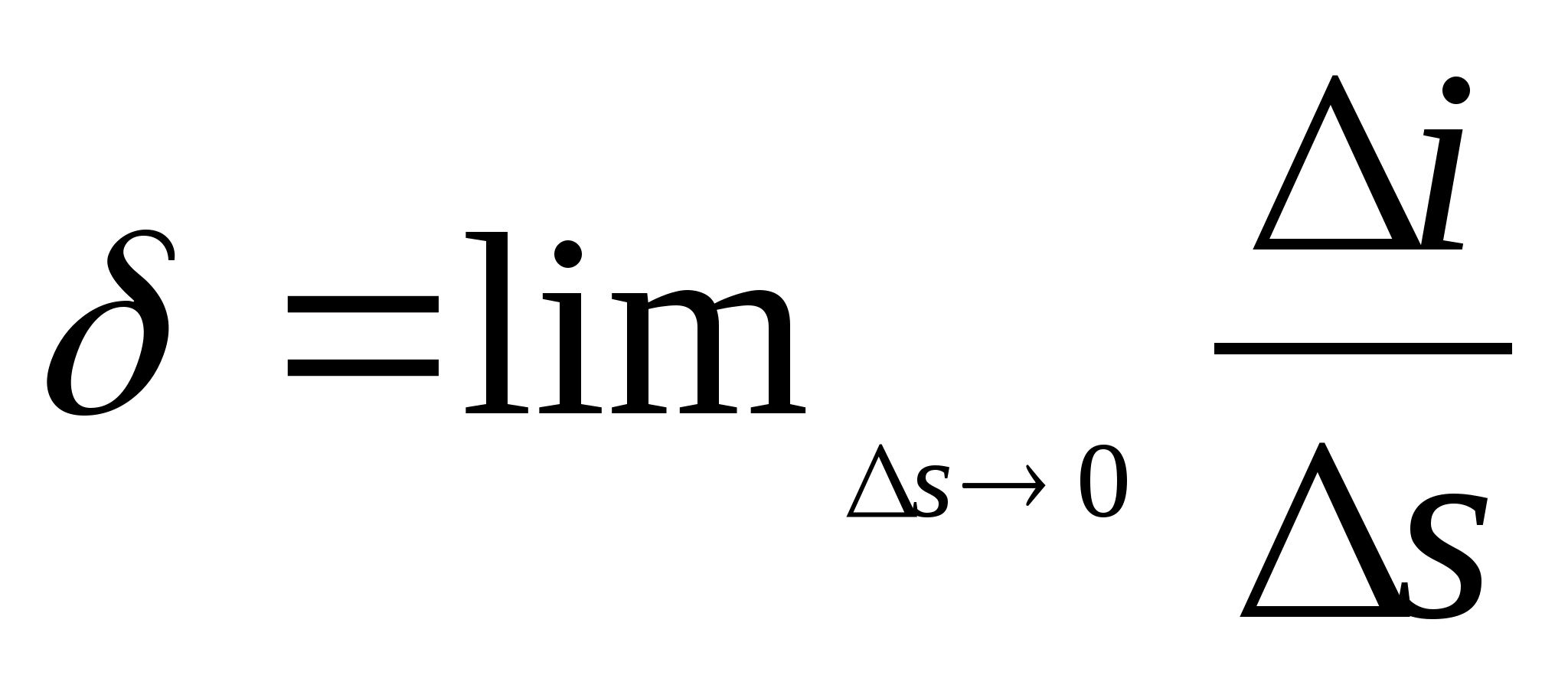 в предположении, что
элементарный
ток i
перпендикулярен
элементарной площадке s
.
Измеряется
в А/м
2 .
в предположении, что
элементарный
ток i
перпендикулярен
элементарной площадке s
.
Измеряется
в А/м
2 .
В
теории поля
в проводящей среде широко используется
понятие тока I
,
представляющего собой поток
вектора
:
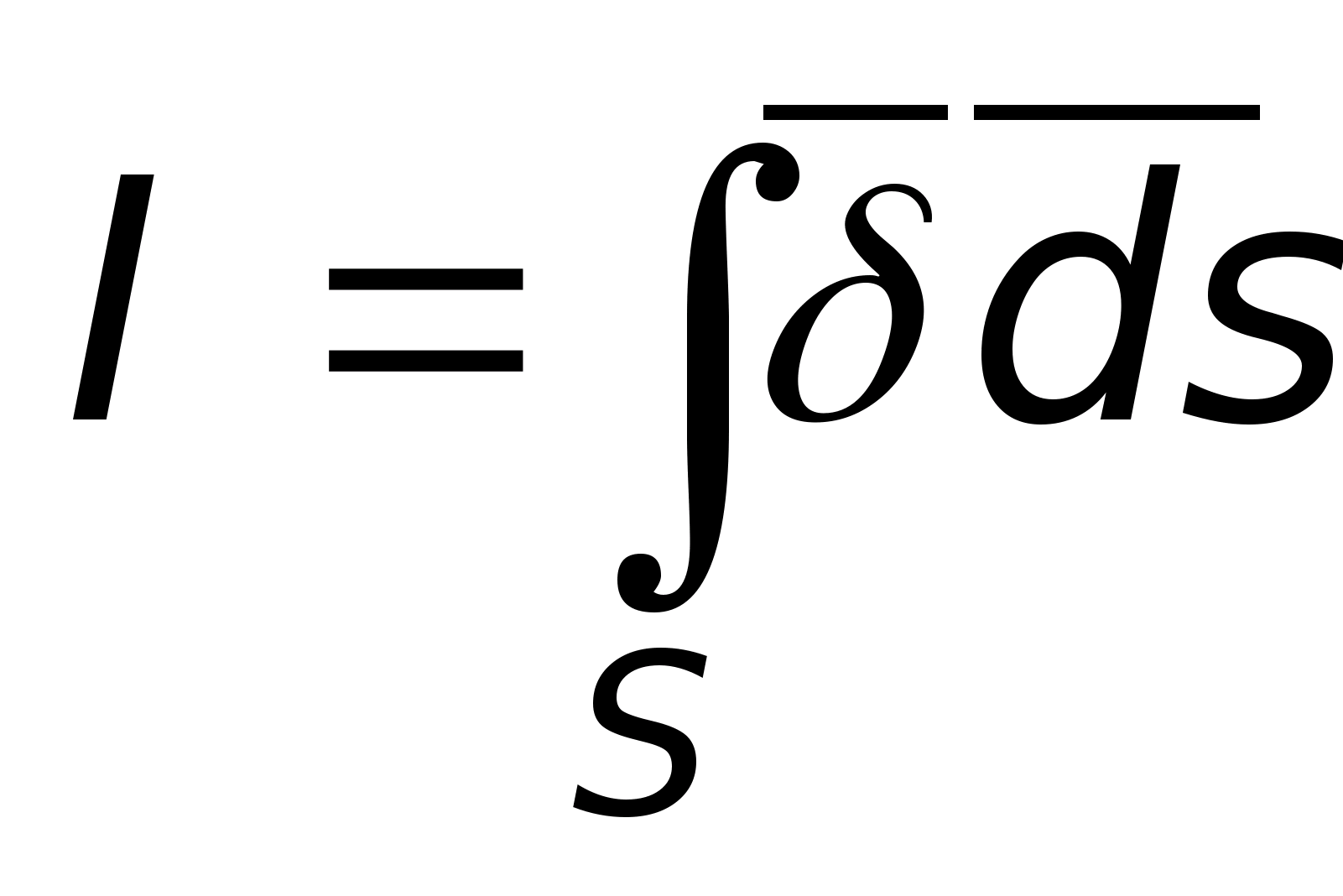 ,
где S
- поверхность, через которую определяется
ток.
В
случае, когда
=const
и
векторы
и ds
совпадают по направлению, I
=
S
.
,
где S
- поверхность, через которую определяется
ток.
В
случае, когда
=const
и
векторы
и ds
совпадают по направлению, I
=
S
.
Законы Ома, Кирхгофа и Джоуля-Ленца в дифференциальной форме
В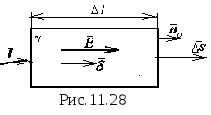 ыделим
мысленно из проводящей среды объём V
в
виде цилиндра очень малых размеров
(рис.11.28). Пусть его длина l
,
поперечное сечение s
.
ыделим
мысленно из проводящей среды объём V
в
виде цилиндра очень малых размеров
(рис.11.28). Пусть его длина l
,
поперечное сечение s
.
Расположим
этот цилиндр так, чтобы его образующая
совпадала с направлением векторов Е
и
.
В силу малости объёма V
можно считать, что векторы
Е
и
неизменны
во всех его точках. Тогда ток, протекающий
по телу цилиндра:
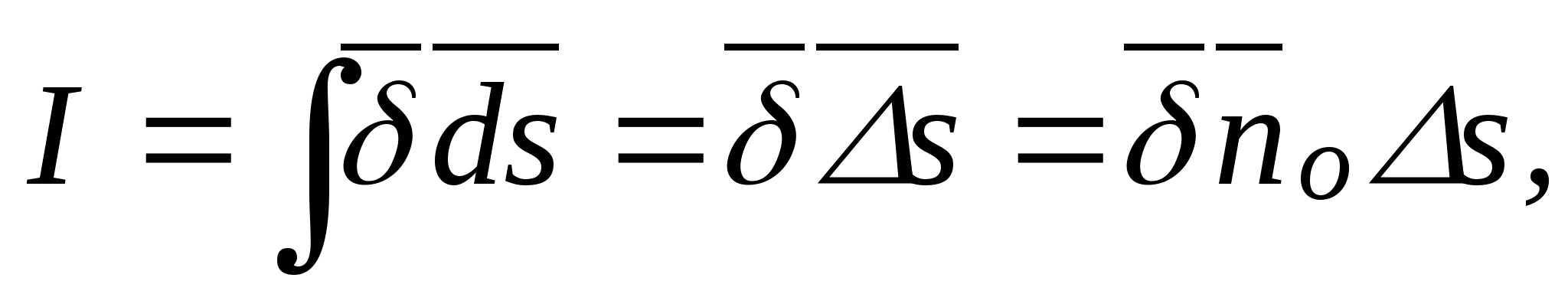 где
где
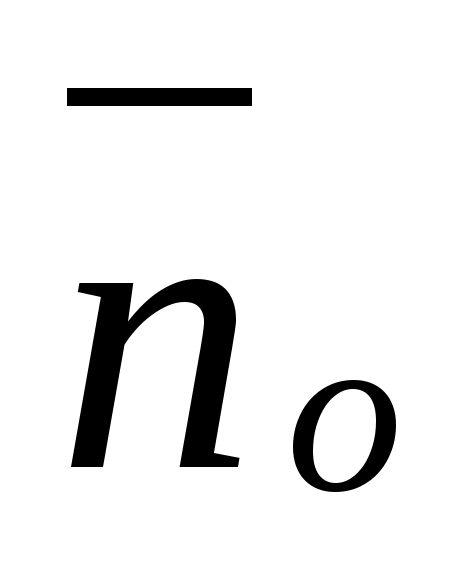 - единичный вектор, имеющий такое же
направление как и векторы Е
,
и s
.
Напряжение между основаниями цилиндра:
- единичный вектор, имеющий такое же
направление как и векторы Е
,
и s
.
Напряжение между основаниями цилиндра:
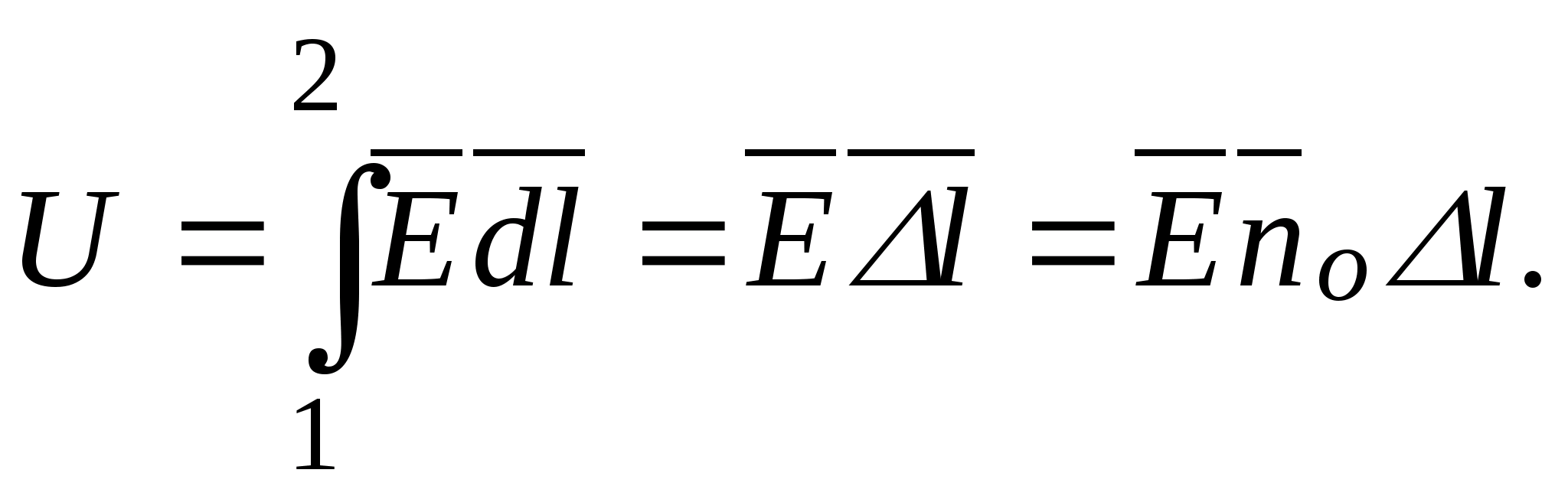 Сопротивление цилиндрического
объёма
Сопротивление цилиндрического
объёма
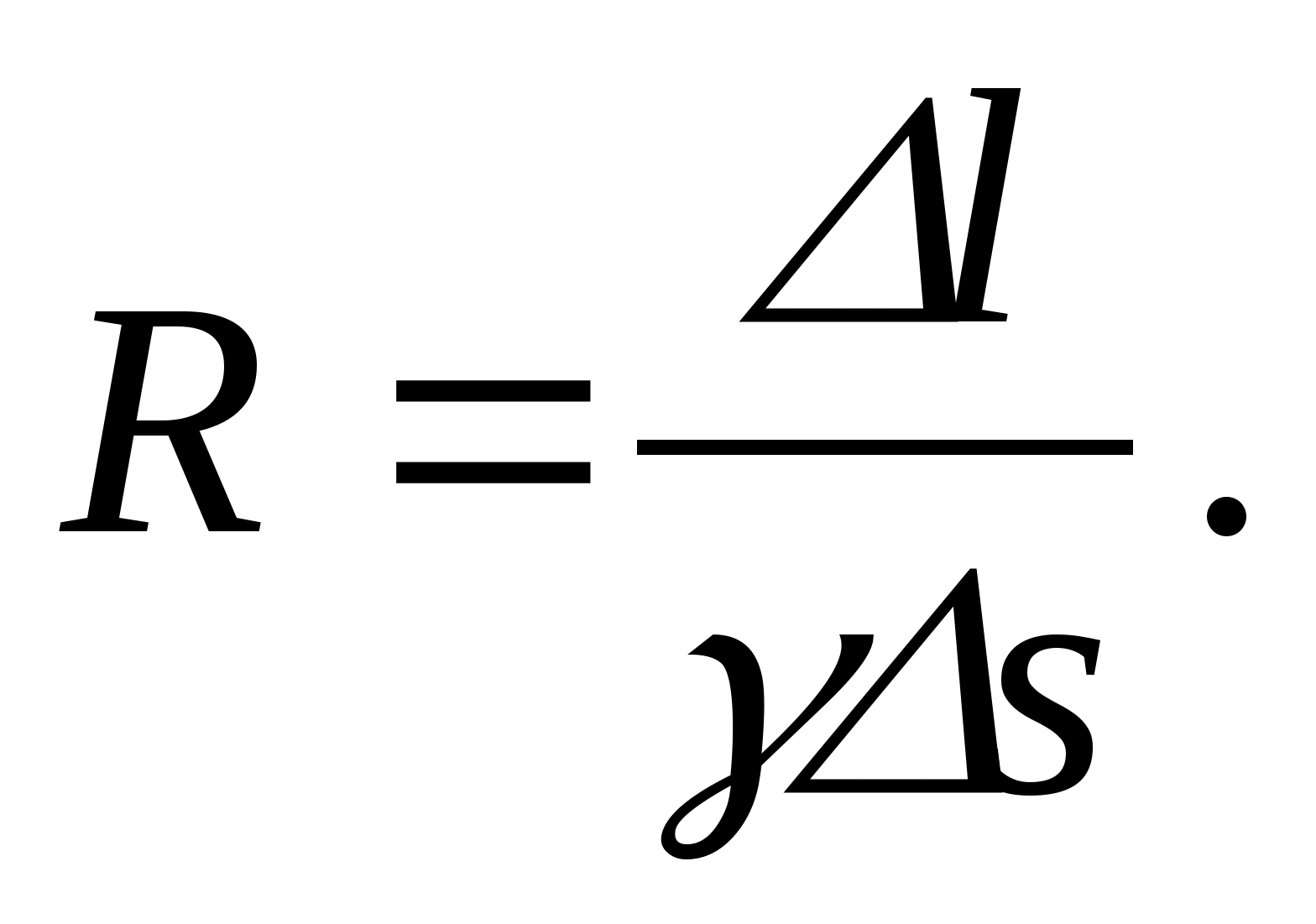 В соответствии с законом Ома в интегральной
форме
В соответствии с законом Ома в интегральной
форме
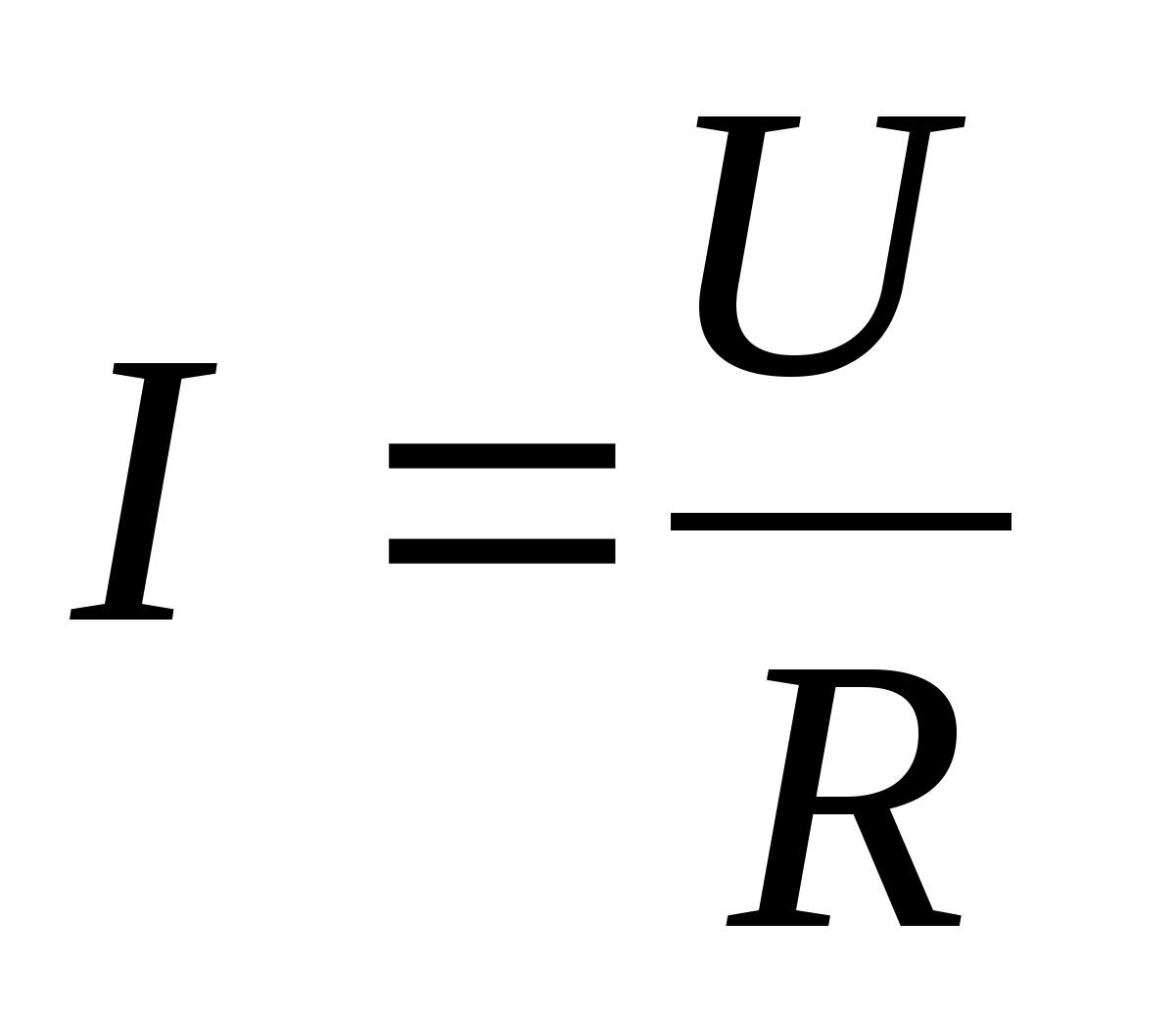 или
или
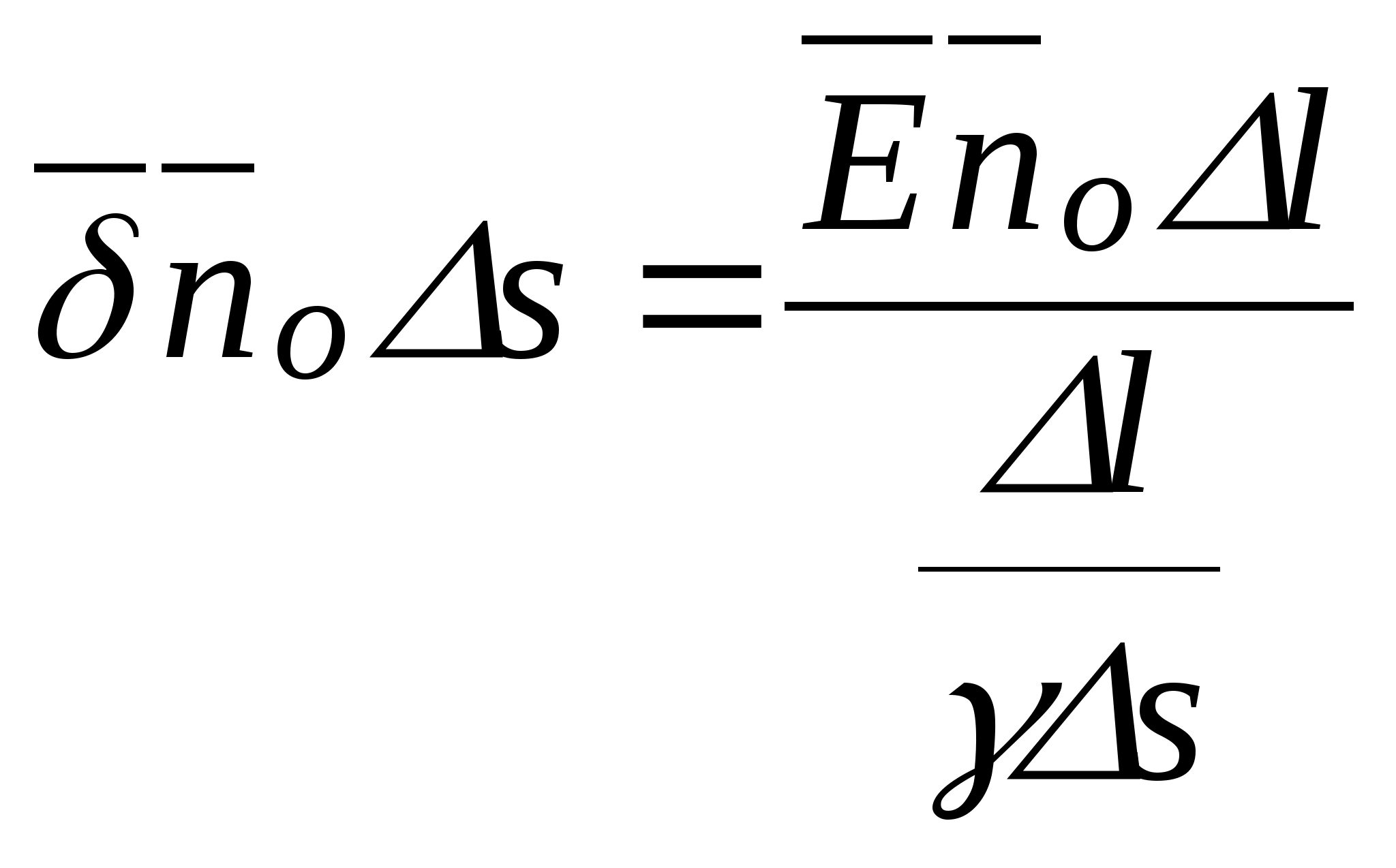 или
или
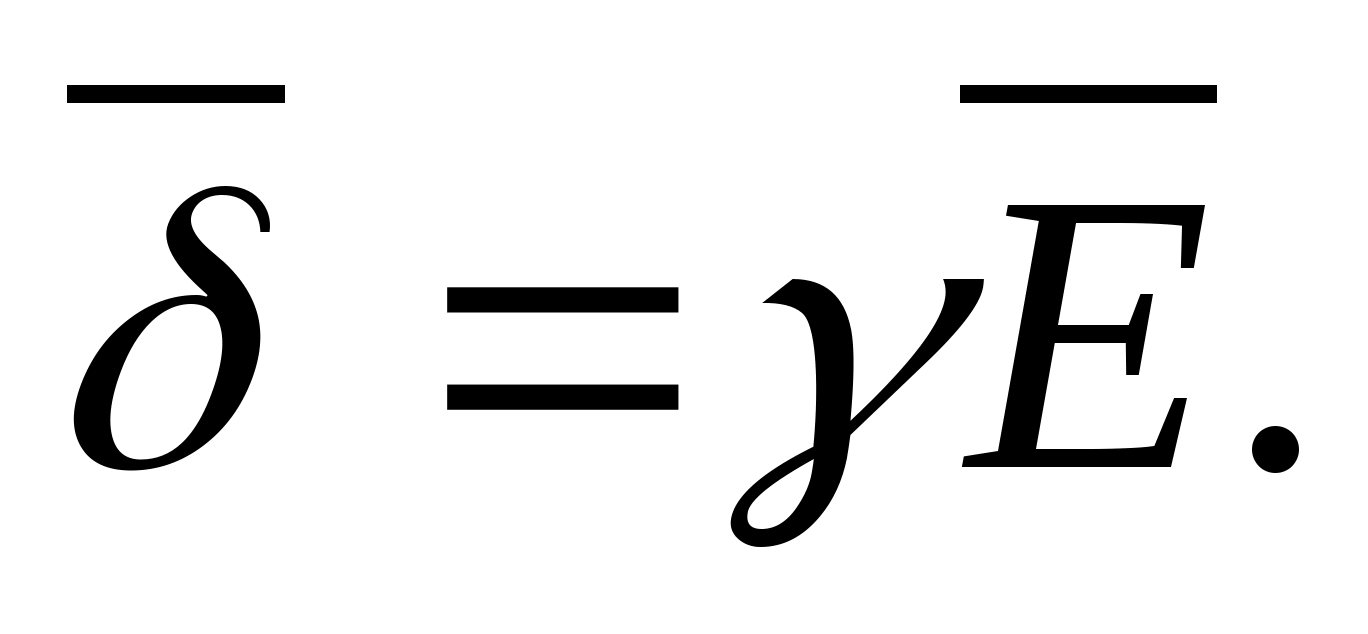 Это и есть
закон Ома в дифференциальной форме.
Это
выражение
называется дифференциальной формой
закона полного тока по той причине, что
даёт
точечную характеристику поля: в конкретной
точке связывает плотность тока и
напряжённость поля. Это выражение
справедливо для областей поля, не занятых
источниками ЭДС. А в областях, занятых
источниками, кроме «кулонова»
(электростатического) поля, существует
ещё так называемое стороннее электрическое
поле. Действительно мы знаем, если в
электростатическое поле внести проводник,
то в нем произойдет перемещение свободных
зарядов. Причем они переместятся
настолько, что создаваемое ими поле
полностью скомпенсирует внешнее поле.
Для того чтобы в проводнике длительно
протекал ток необходимо наличие
электрического поля, силы которого
непрерывно перемещали бы свободные
заряды. Такое поле может быть создано
и поддерживаться силами неэлектрического
происхождения (термоэлектрическими,
химическими и т.д.), Иными словами
стороннее поле всегда связано с источником
энергии, который преобразует какую-либо
энергию в электричество. Напряженность
стороннего поля Е
стор
определяется как предел отношения силы,
действующей на заряд, стремящийся к
нулю, со стороны стороннего поля к
величине этого заряда. Если в проводнике
действуют одновременно и «кулоново» и
стороннее поле, то напряженность
результирующего поля будет
Это и есть
закон Ома в дифференциальной форме.
Это
выражение
называется дифференциальной формой
закона полного тока по той причине, что
даёт
точечную характеристику поля: в конкретной
точке связывает плотность тока и
напряжённость поля. Это выражение
справедливо для областей поля, не занятых
источниками ЭДС. А в областях, занятых
источниками, кроме «кулонова»
(электростатического) поля, существует
ещё так называемое стороннее электрическое
поле. Действительно мы знаем, если в
электростатическое поле внести проводник,
то в нем произойдет перемещение свободных
зарядов. Причем они переместятся
настолько, что создаваемое ими поле
полностью скомпенсирует внешнее поле.
Для того чтобы в проводнике длительно
протекал ток необходимо наличие
электрического поля, силы которого
непрерывно перемещали бы свободные
заряды. Такое поле может быть создано
и поддерживаться силами неэлектрического
происхождения (термоэлектрическими,
химическими и т.д.), Иными словами
стороннее поле всегда связано с источником
энергии, который преобразует какую-либо
энергию в электричество. Напряженность
стороннего поля Е
стор
определяется как предел отношения силы,
действующей на заряд, стремящийся к
нулю, со стороны стороннего поля к
величине этого заряда. Если в проводнике
действуют одновременно и «кулоново» и
стороннее поле, то напряженность
результирующего поля будет
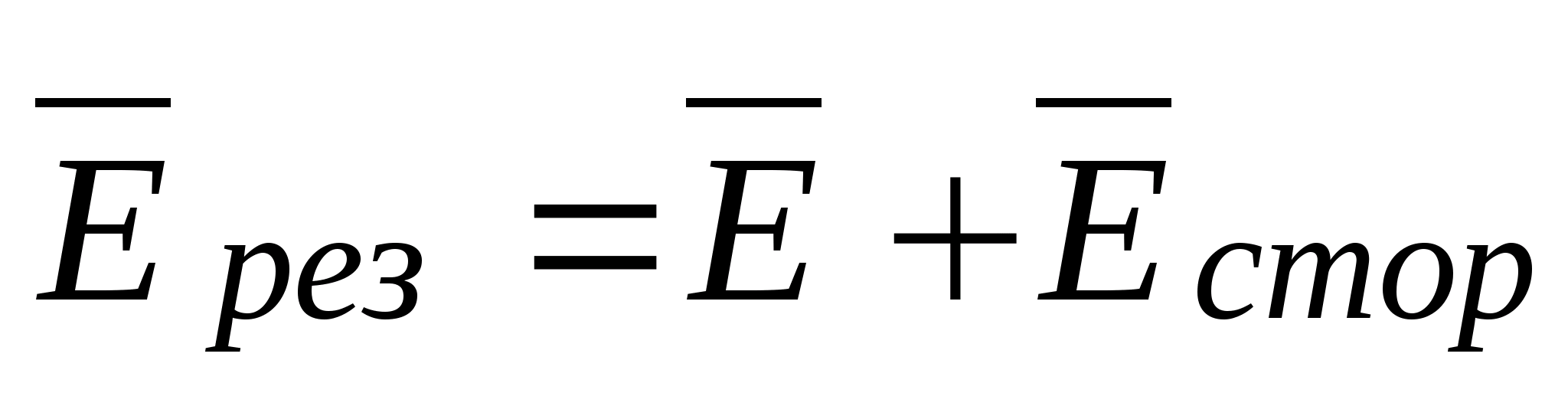 .
И тогда выражение закона Ома принимает
вид
.
И тогда выражение закона Ома принимает
вид
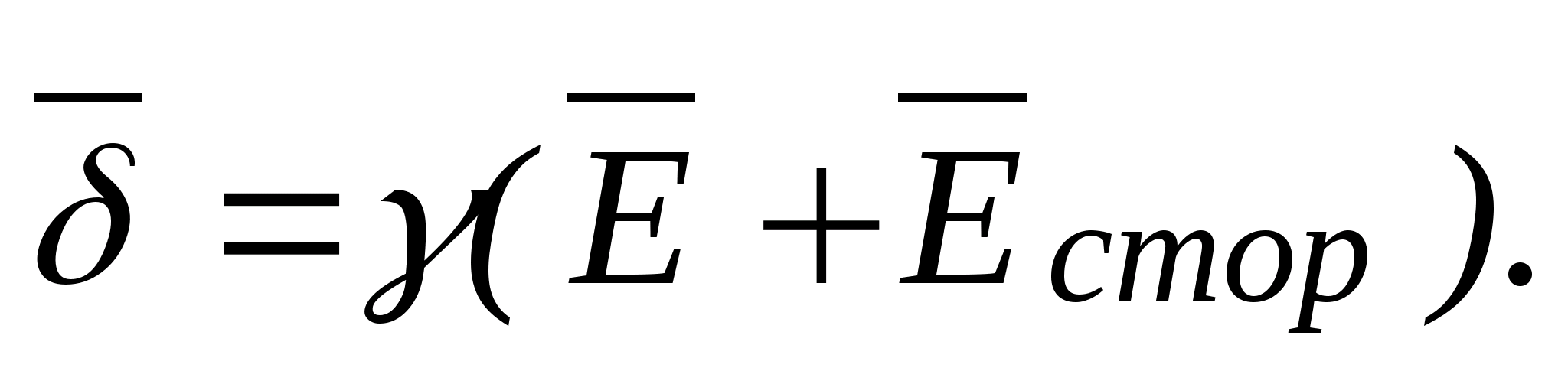 Это выражение называется обобщенным
законом Ома в дифференциальной форме
или вторым законом Кирхгофа.
Это выражение называется обобщенным
законом Ома в дифференциальной форме
или вторым законом Кирхгофа.
Если
в проводящей среде выделить некоторый
замкнутый объём, по которому протекает
постоянный ток, то понятно, что ток,
который войдет в объём, должен равняться
току, вышедшему из него иначе в этом
объёме происходило бы накопление или
уменьшение электрических зарядов, что
опытом не подтверждается. Иными словами
сумма входящих и выходящих из объёма
токов равна нулю, что математически
записывается так
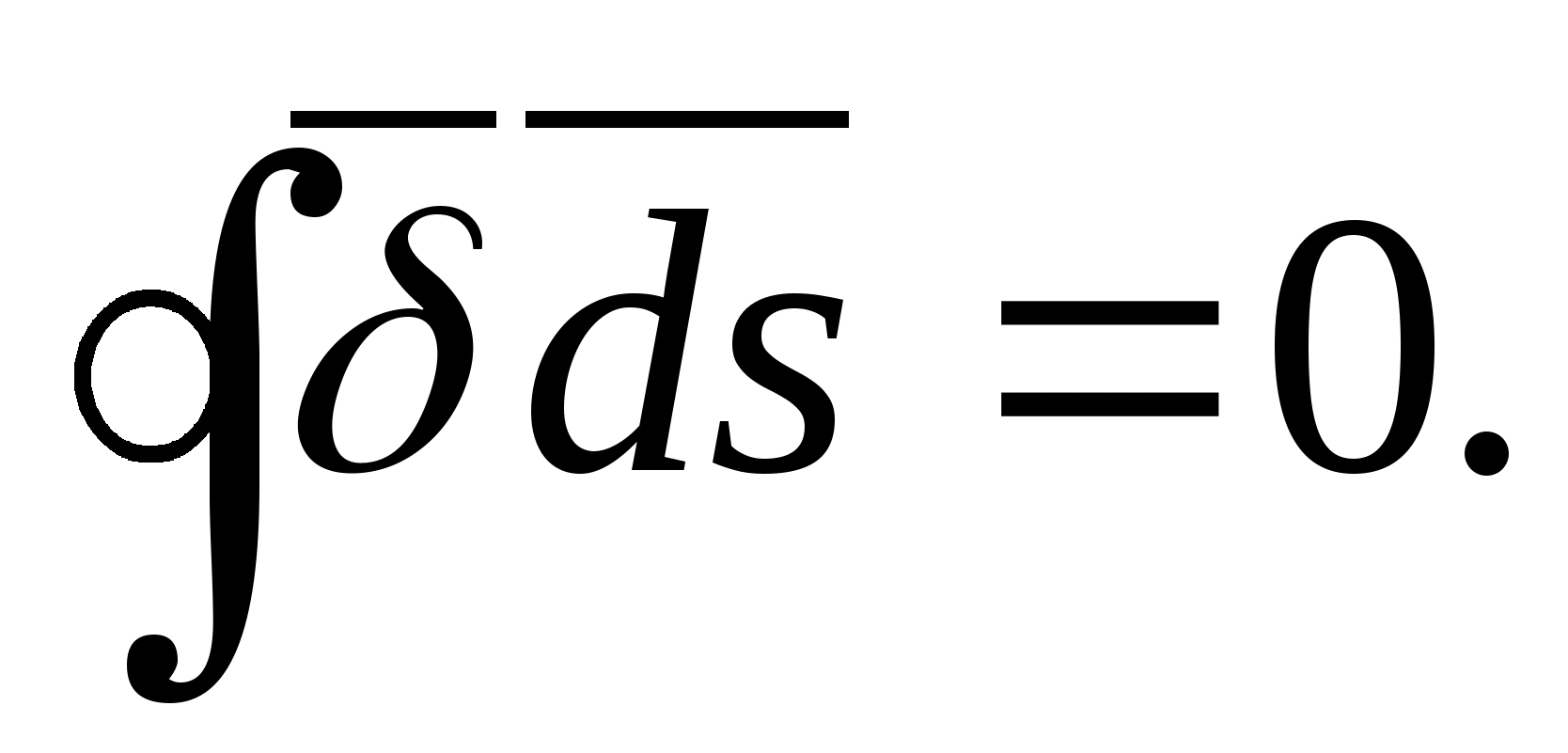 Это соотношение останется справедливым,
если взять предел отношения потока
вектора
к стремящемуся к нулю объёму, ограниченному
поверхностью интегрирования
Это соотношение останется справедливым,
если взять предел отношения потока
вектора
к стремящемуся к нулю объёму, ограниченному
поверхностью интегрирования
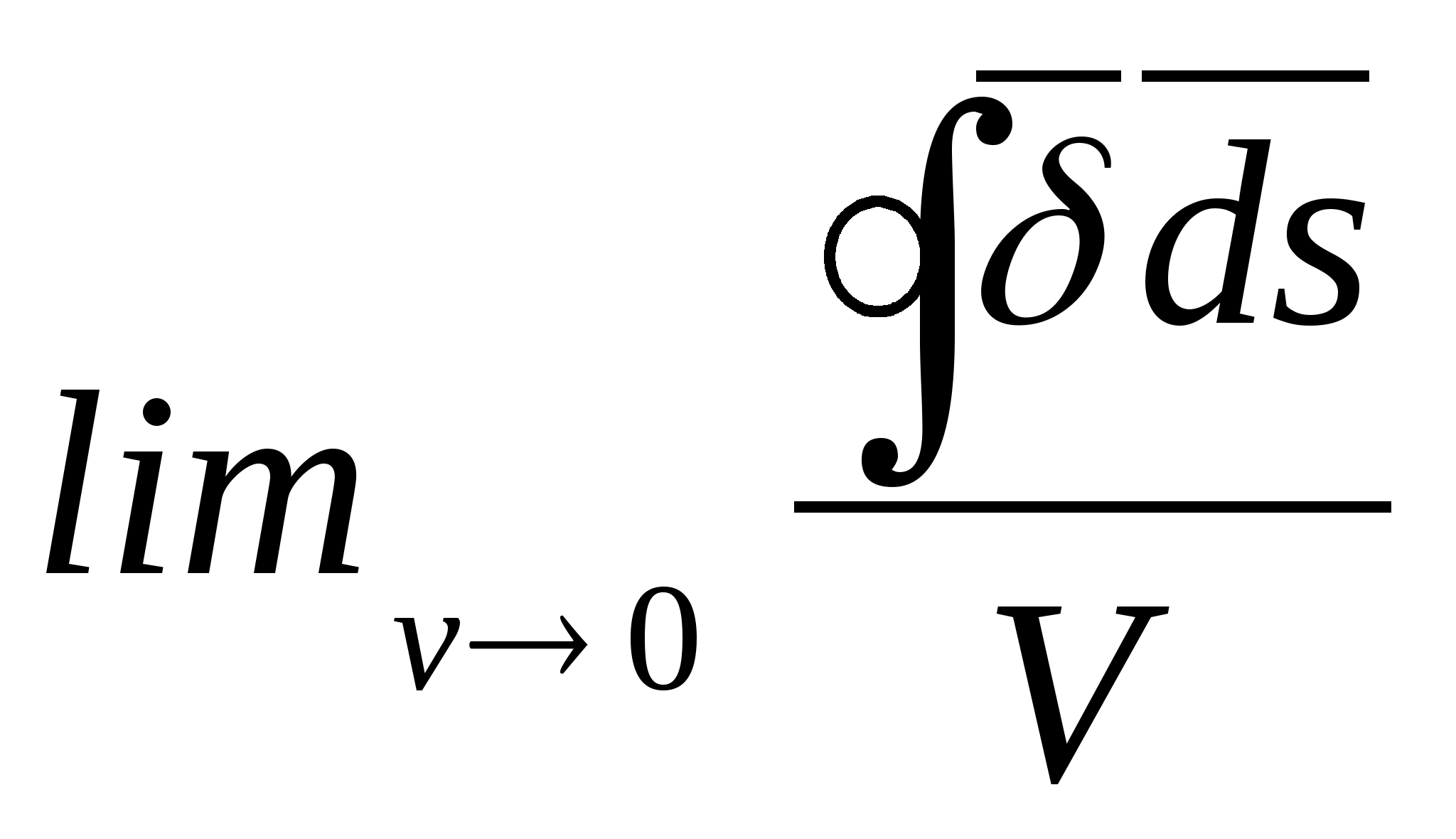 или
или
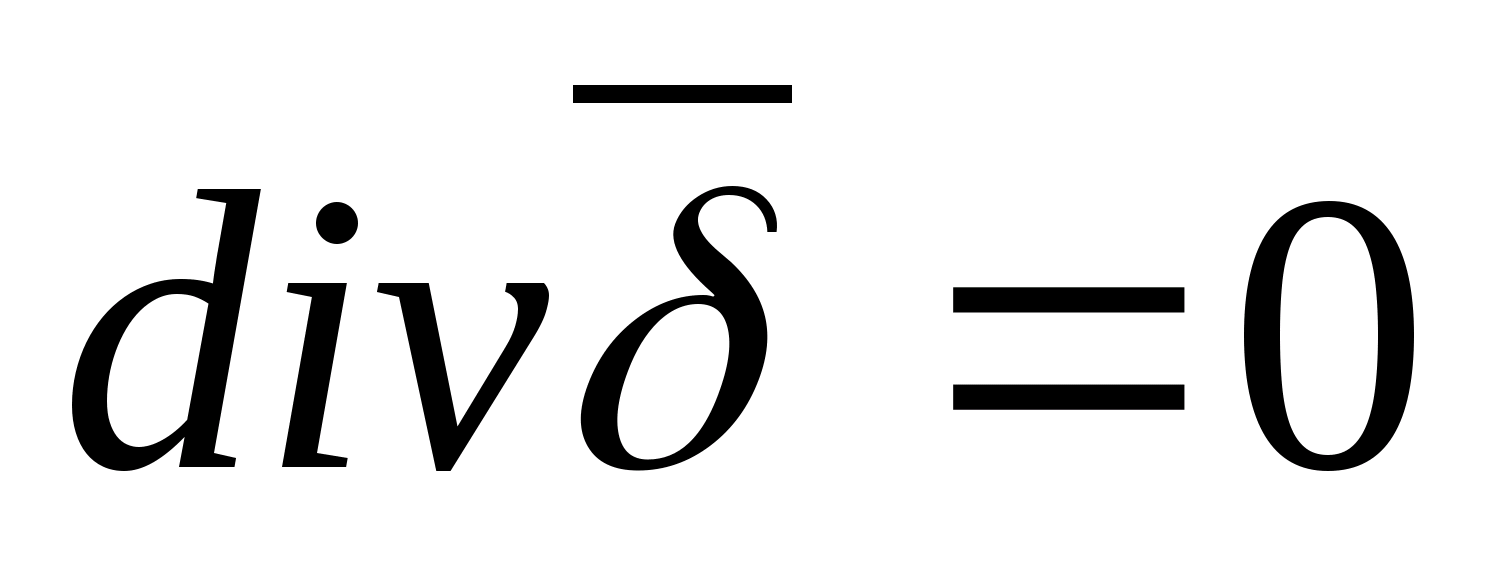 .
Это выражение называется первым законом
Кирхгофа в дифференциальной форме. Это
уравнение говорит о том, что в любой
точке поля в проводящей среде нет ни
стока, ни истока линий вектора
,
или линии вектора
являются линиями непрерывными, замкнутыми
сами на себя. Поэтому данное уравнение
называют ещё уравнением непрерывности
линий вектора
.
.
Это выражение называется первым законом
Кирхгофа в дифференциальной форме. Это
уравнение говорит о том, что в любой
точке поля в проводящей среде нет ни
стока, ни истока линий вектора
,
или линии вектора
являются линиями непрерывными, замкнутыми
сами на себя. Поэтому данное уравнение
называют ещё уравнением непрерывности
линий вектора
.
Если
по какому –либо проводнику с сопротивлением
R
протекает постоянный ток I
,
в нем выделяется мощность
Р=
I
2 R
.
Определим
мощность, выделяющуюся в единице объёма
проводящей среды
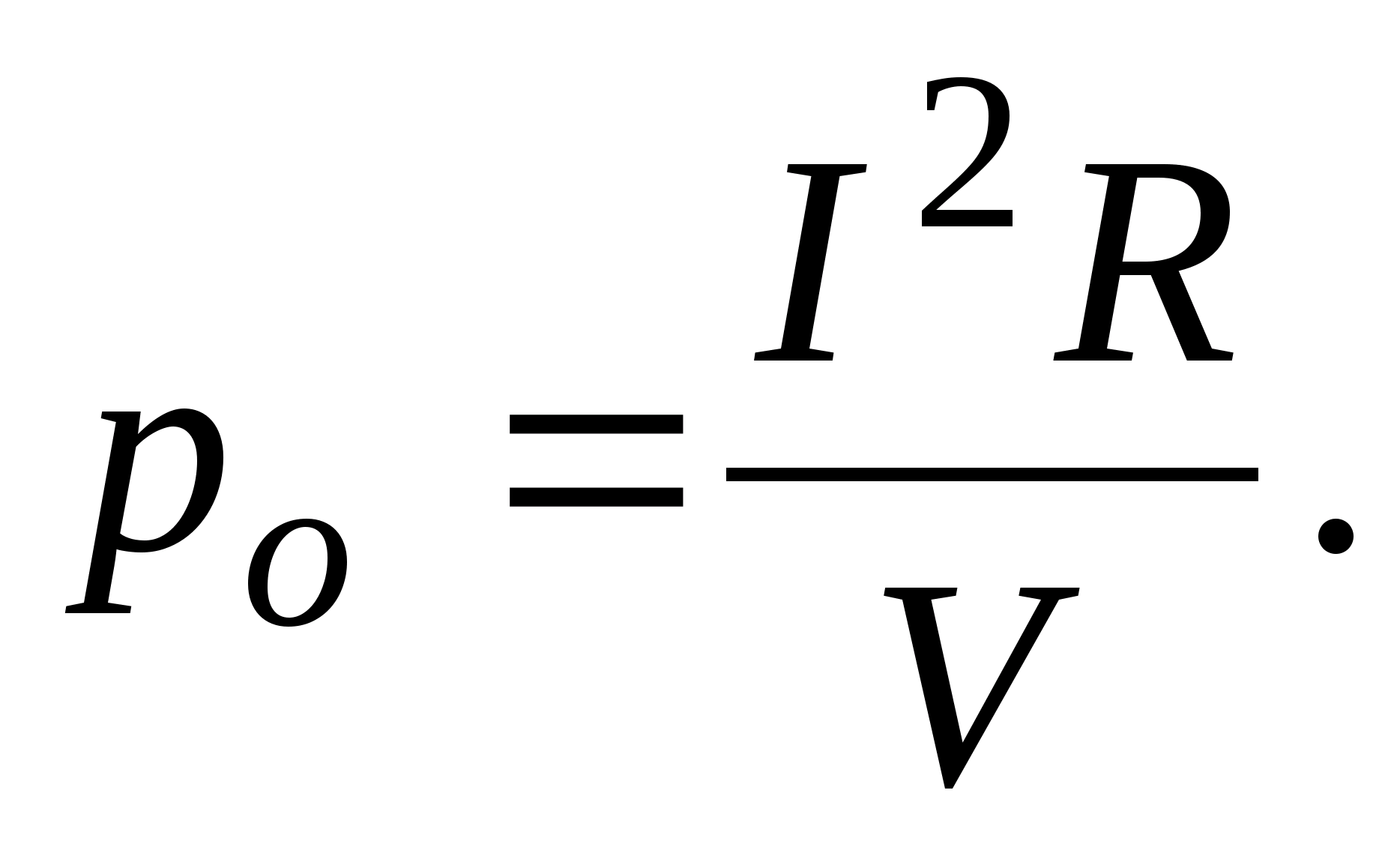 В качестве объёма V
возьмем цилиндр рис.11.28. В этом цилиндре
В качестве объёма V
возьмем цилиндр рис.11.28. В этом цилиндре
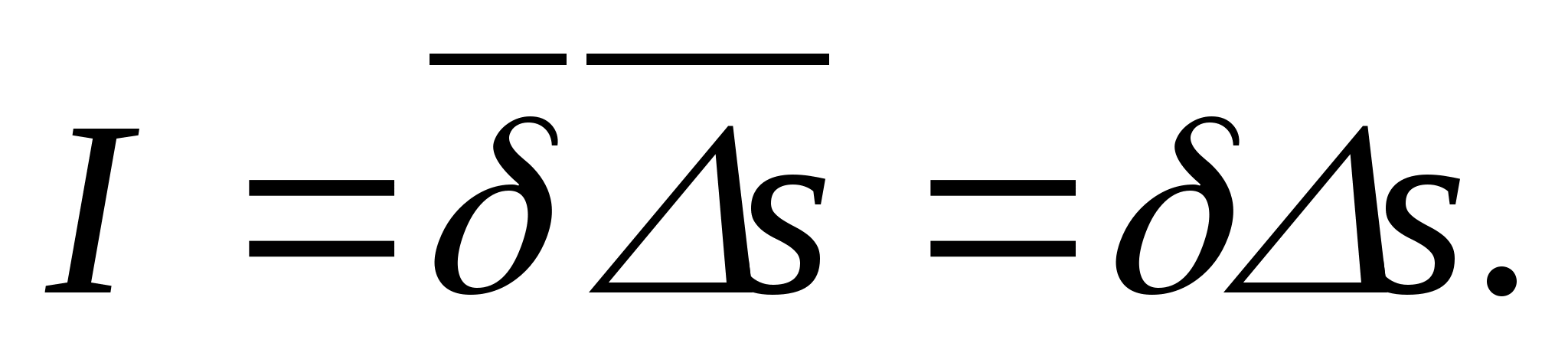 .
Его сопротивление
.
Его сопротивление
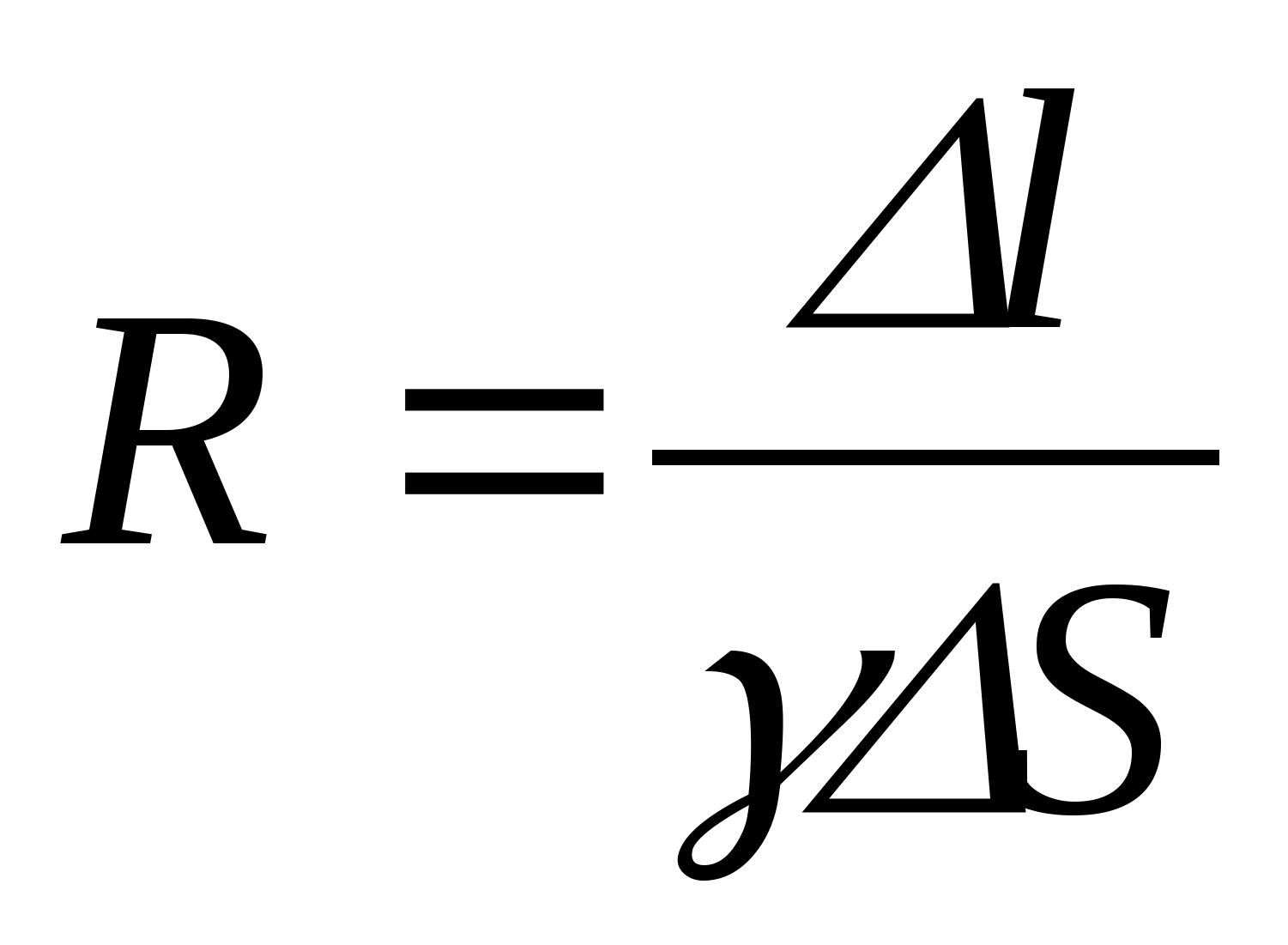 и объём
и объём
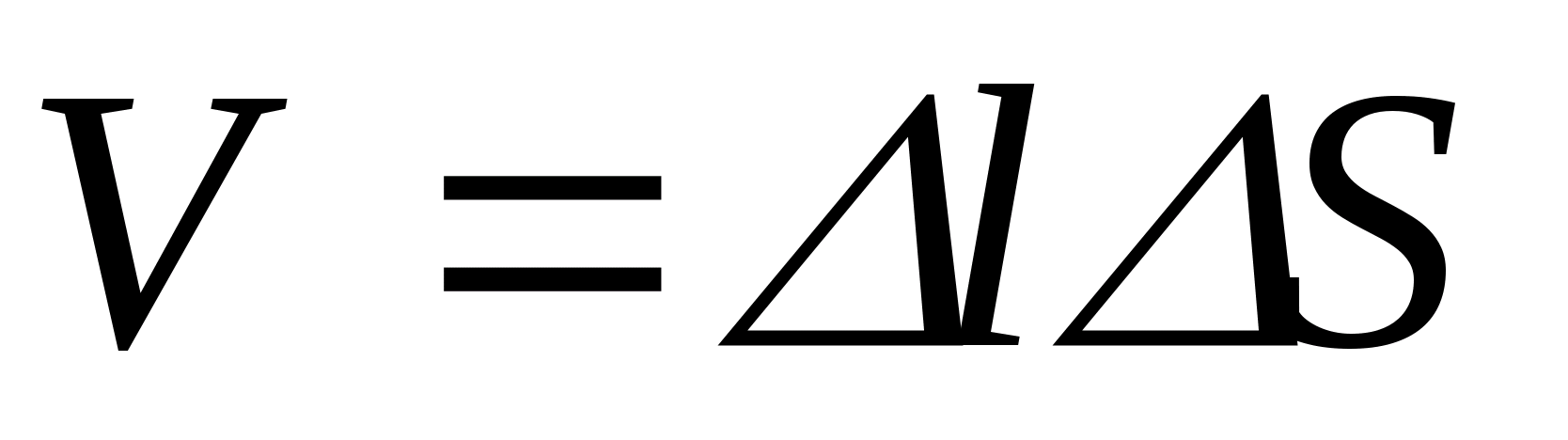 .
Тогда
.
Тогда
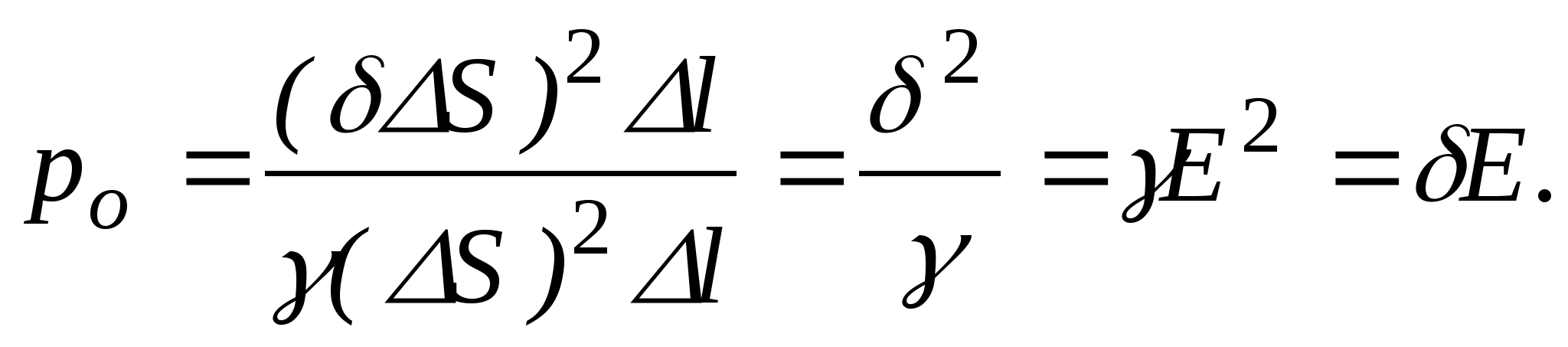 Это и есть закон Джоуля-Ленца в
дифференциальной форме. Мощность
тепловых потерь в объёме конечных
размеров может быть определена по
формуле
Это и есть закон Джоуля-Ленца в
дифференциальной форме. Мощность
тепловых потерь в объёме конечных
размеров может быть определена по
формуле
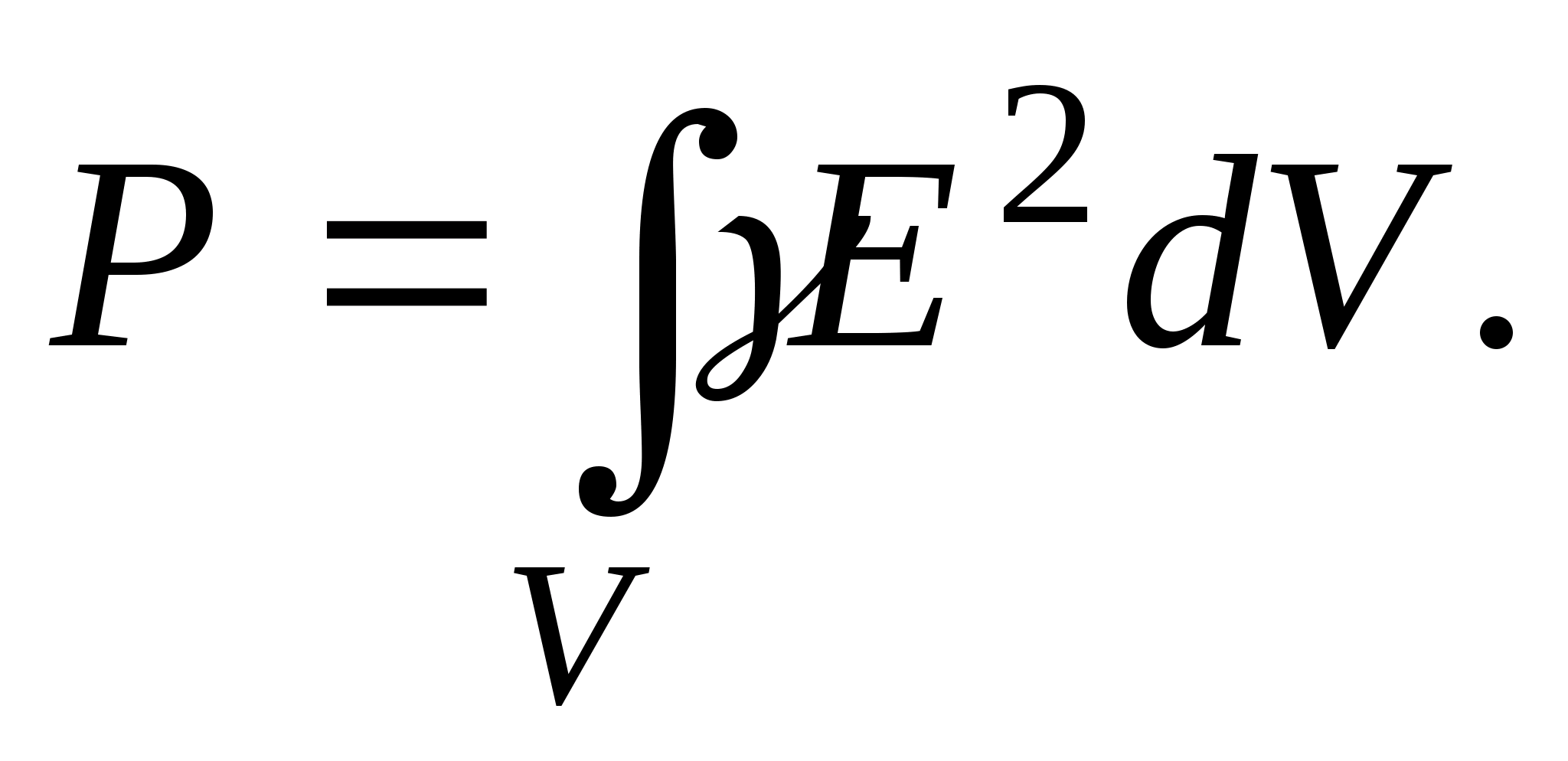
Граничные условия в поле в проводящей среде
В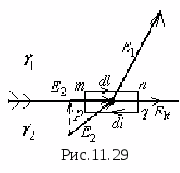 ыясним
какие условия выполняются при переходе
тока из среды с одной удельной проводимостью
в среду с другой проводимостью. На
границе, разделяющей две различные
проводящие среды выполняются два
условия, которые сформулируем одним
предложением: для всех точек, являющихся
общими для этих сред равны по величине
тангенциальные составляющие вектора
Е
и нормальные
составляющие вектора
.
Для доказательства первого условия
окружим любую точку, находящуюся на
границе между средами, бесконечно малым
(длина
- dl
)
плоским (высота бесконечно
мала по сравнению с длиной) контуром
mnpq
и составим выражение циркуляции вектора
Е
для этого
контура (рис.11.29). Сторона mn
находится в верхней
среде и, если контур обходить по часовой
стрелке, то составляющая циркуляции
вдоль этой стороны
.Аналогично
для стороны.
Через боковые грани потоком вектора
можно пренебречь из-за малости этих
граней, а через верхнюю и нижнюю –
соответственно
ыясним
какие условия выполняются при переходе
тока из среды с одной удельной проводимостью
в среду с другой проводимостью. На
границе, разделяющей две различные
проводящие среды выполняются два
условия, которые сформулируем одним
предложением: для всех точек, являющихся
общими для этих сред равны по величине
тангенциальные составляющие вектора
Е
и нормальные
составляющие вектора
.
Для доказательства первого условия
окружим любую точку, находящуюся на
границе между средами, бесконечно малым
(длина
- dl
)
плоским (высота бесконечно
мала по сравнению с длиной) контуром
mnpq
и составим выражение циркуляции вектора
Е
для этого
контура (рис.11.29). Сторона mn
находится в верхней
среде и, если контур обходить по часовой
стрелке, то составляющая циркуляции
вдоль этой стороны
.Аналогично
для стороны.
Через боковые грани потоком вектора
можно пренебречь из-за малости этих
граней, а через верхнюю и нижнюю –
соответственно
По своей природе электростатическое поле и поле постоянного тока в проводящей среде совершенно различны. Электростатическое поле создается неподвижными и неизменными во времени зарядами, а поле в проводящей среде – это поле зарядов, имеющих упорядоченное движение под действием внешнего источника. Тем не менее между этими двумя полями может быть проведена формальная аналогия, которая заключается в следующем.
1.Электростатическое
поле в областях, не занятых зарядом, и
поле в проводящей среде в областях,
свободных от источников ЭДС, описываются
одним и тем же уравнением – уравнением
Лапласа. Для электростатического поля
мы уже показывали, что
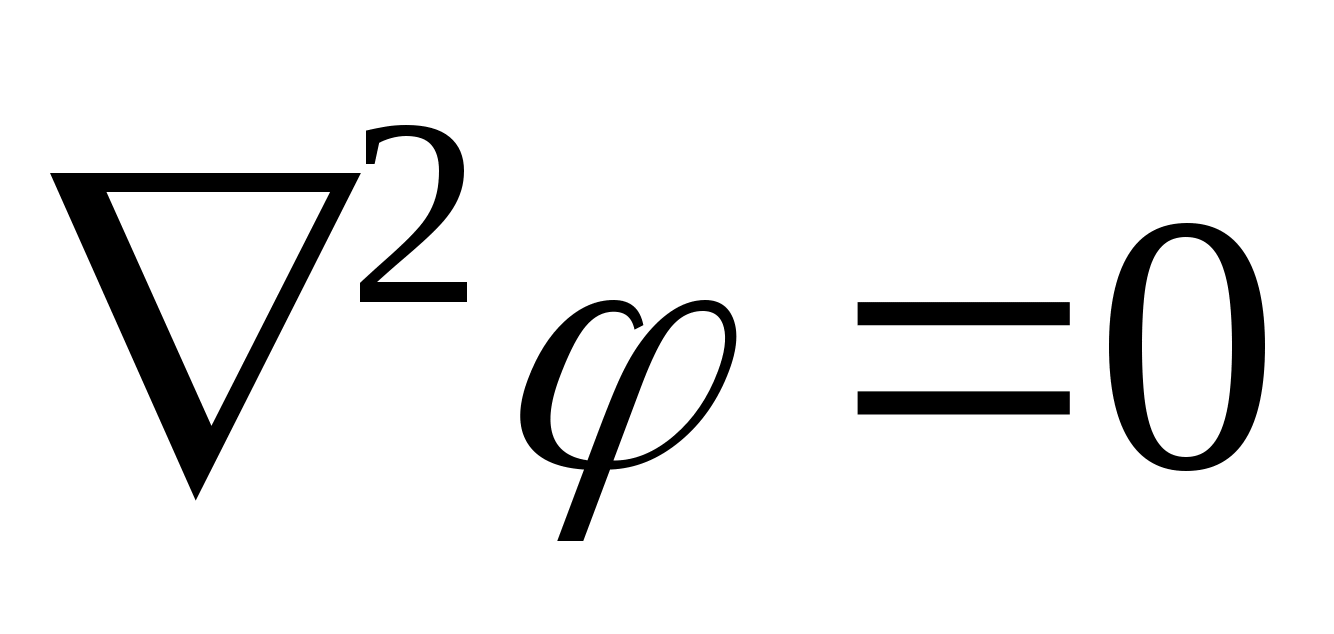 .
Покажем
это для поля в проводящей среде, в котором
.
Покажем
это для поля в проводящей среде, в котором
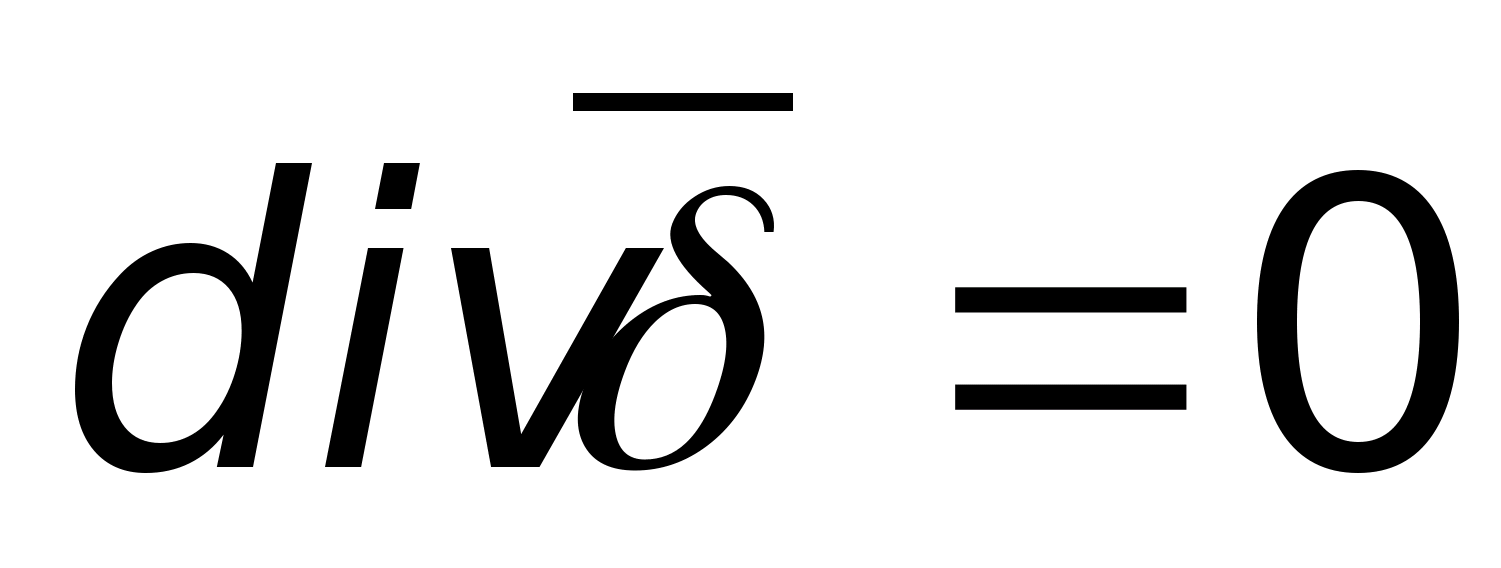 ,
а
Тогда
,
а
Тогда
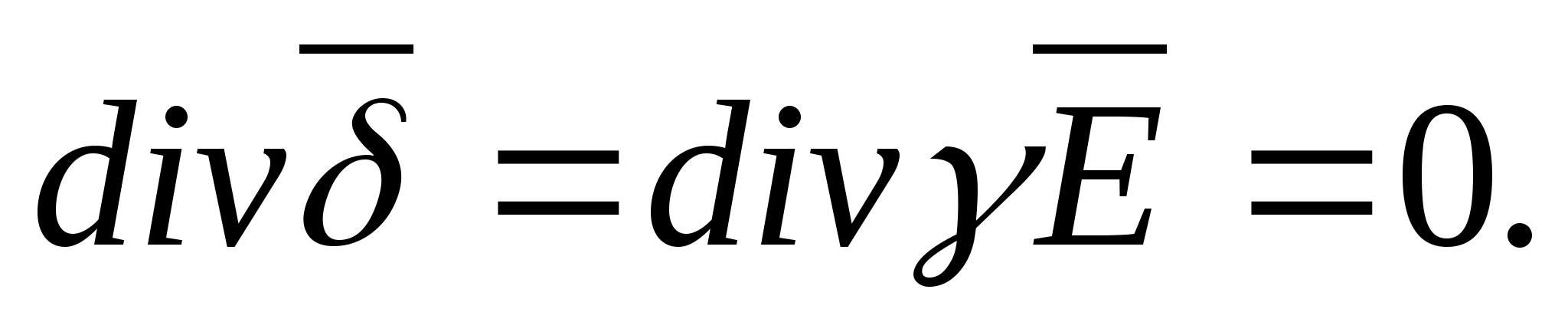 Если среда однородна и изотропна, то
является постоянной величиной, ее можно
вынести за знак дивергенции, которая и
должна давать ноль, т.е.
Если среда однородна и изотропна, то
является постоянной величиной, ее можно
вынести за знак дивергенции, которая и
должна давать ноль, т.е.
3. В этих полях выполняются одинаковые граничные условия для сходных величин: в электростатике Е 1 t =Е 2 t и D 1 n =D 2 n , в проводящей среде Е 1 t =Е 2 t и 1 n = 2 n .
Н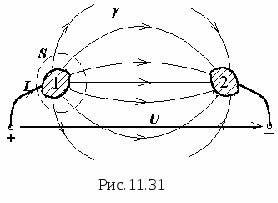 о
если
два поля удовлетворяют одному и тому
же уравнению и в них выполняются
одинаковые граничные условия для сходных
величин, то поля тождественны, т.е. в них
одинаковы совокупности силовых и
эквипотенциальных линий при одинаковой
форме граничных поверхностей. Эта
формальная аналогия очень широко
используется на практике. Так, если
какое-либо электростатическое поле
изучено, то все сведения о нем могут
быть перенесены на геометрически
подобное поле в проводящей среде.
Справедлив, конечно, и обратный перенос.
Эта аналогия лежит в основе моделирования
одних полей другими (чаще всего
электростатических полей – полем в
проводящей среде). Указанная аналогия
позволяет пользоваться формулами,
полученными при расчете электростатических
полей, и в случае поля в проводящей
среде. В частности, формулы для проводимости
между электродами, помещенными в
проводящую среду, могут быть получены
из формул ёмкости между такими же
электродами в электростатическом поле.
Покажем это. Если два электрода поместить
в проводящую среду и подвести к ним
питание от источника с напряжением U
S
.
Тогда согласно теореме Гаусса в
интегральной форме
о
если
два поля удовлетворяют одному и тому
же уравнению и в них выполняются
одинаковые граничные условия для сходных
величин, то поля тождественны, т.е. в них
одинаковы совокупности силовых и
эквипотенциальных линий при одинаковой
форме граничных поверхностей. Эта
формальная аналогия очень широко
используется на практике. Так, если
какое-либо электростатическое поле
изучено, то все сведения о нем могут
быть перенесены на геометрически
подобное поле в проводящей среде.
Справедлив, конечно, и обратный перенос.
Эта аналогия лежит в основе моделирования
одних полей другими (чаще всего
электростатических полей – полем в
проводящей среде). Указанная аналогия
позволяет пользоваться формулами,
полученными при расчете электростатических
полей, и в случае поля в проводящей
среде. В частности, формулы для проводимости
между электродами, помещенными в
проводящую среду, могут быть получены
из формул ёмкости между такими же
электродами в электростатическом поле.
Покажем это. Если два электрода поместить
в проводящую среду и подвести к ним
питание от источника с напряжением U
S
.
Тогда согласно теореме Гаусса в
интегральной форме
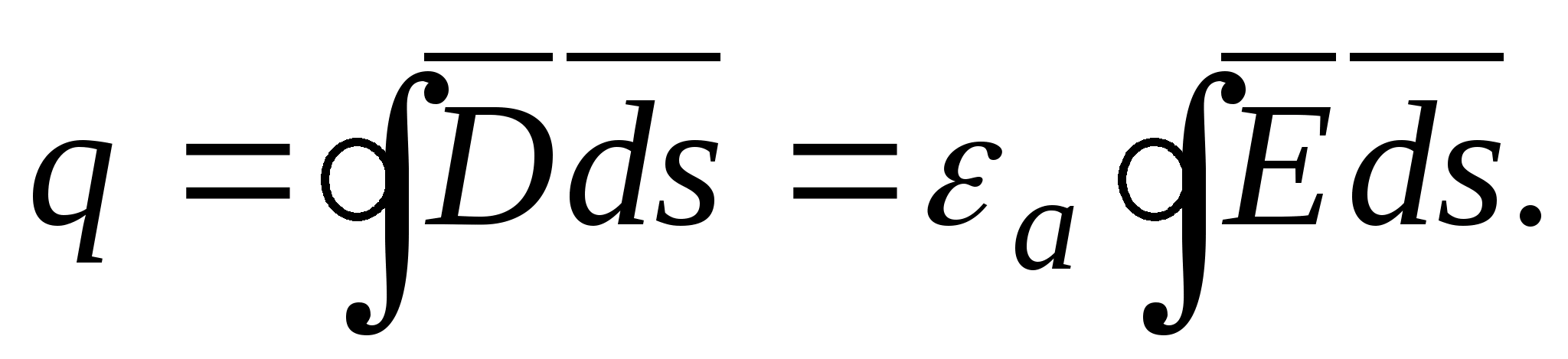 А
А
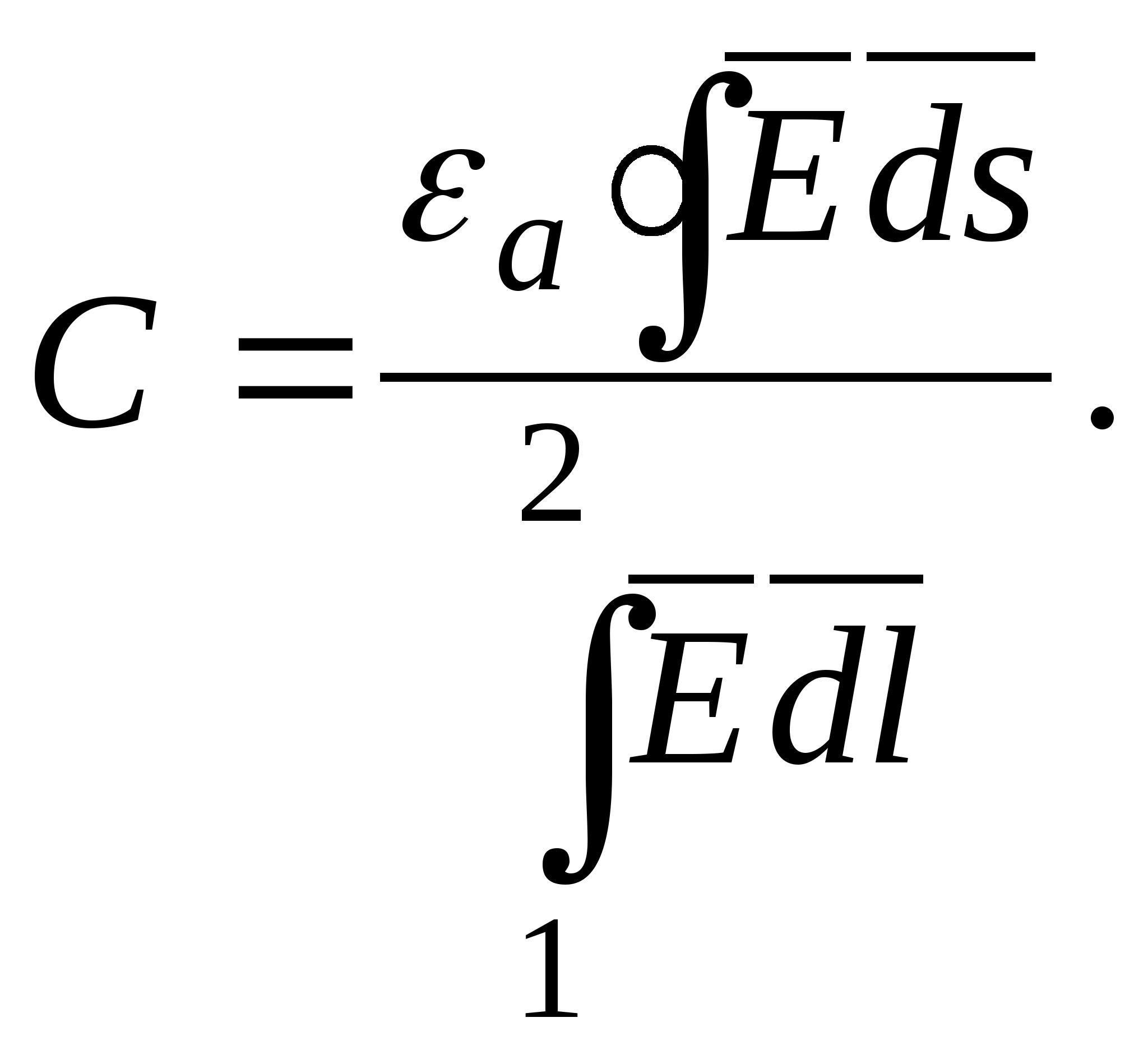
С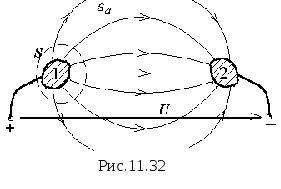 равнивая
выражения для G
и С
,
видим, что они отличаются тем, что в них
и а
меняются местами. Это соотношение можно
записать так
равнивая
выражения для G
и С
,
видим, что они отличаются тем, что в них
и а
меняются местами. Это соотношение можно
записать так
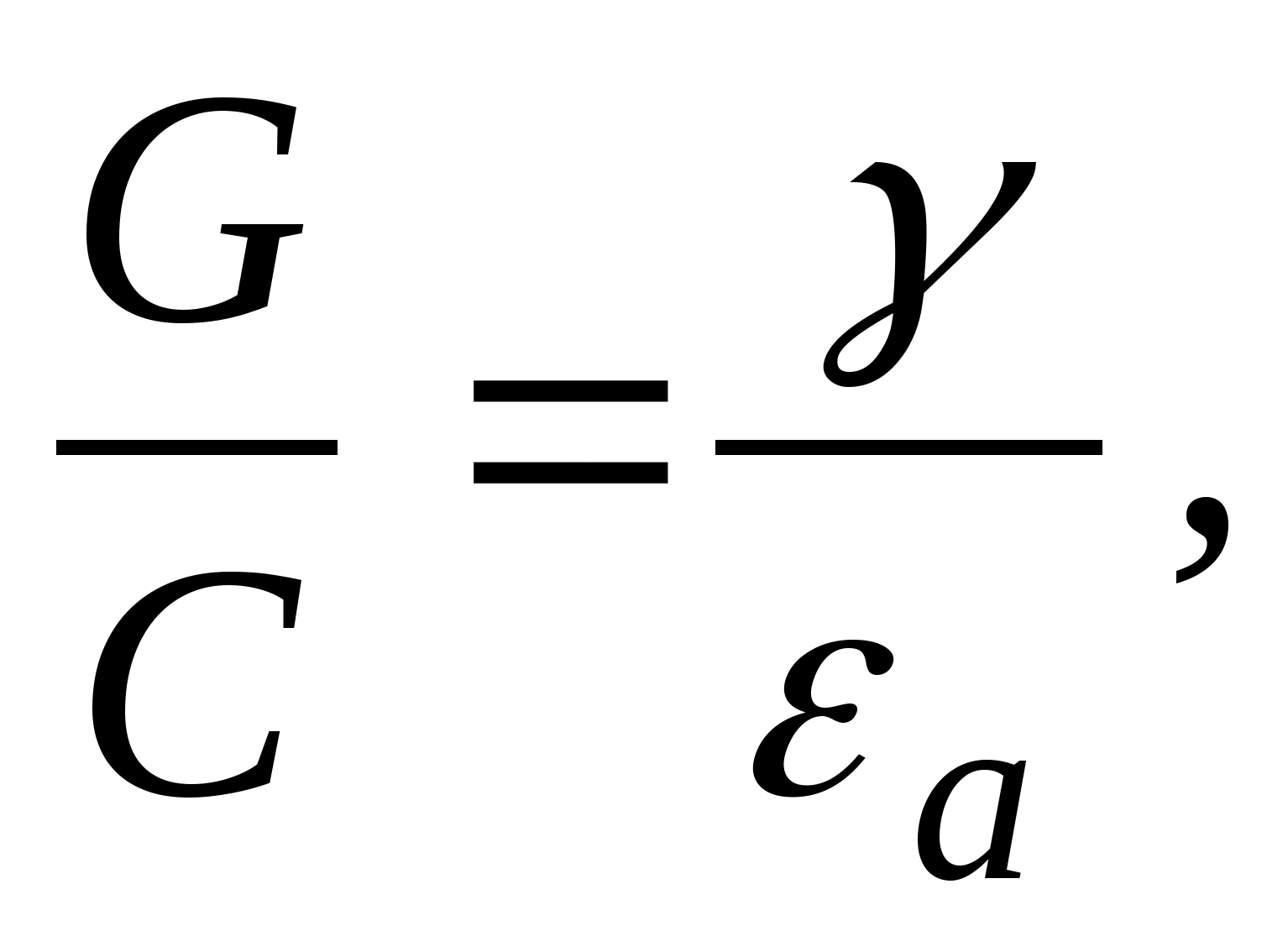 что говорит о том, что если в формуле
ёмкости
а
заменить на
,
то получим формулу для определения G
.
Конечно
возможен и обратный переход.
что говорит о том, что если в формуле
ёмкости
а
заменить на
,
то получим формулу для определения G
.
Конечно
возможен и обратный переход.
Р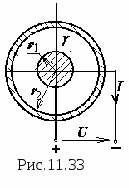 ассмотрим
конкретный пример. Изоляция коаксиального
кабеля не бывает идеальной. Практически
она обладает некоторой хотя и очень
малой удельной проводимостью
.
В связи с этим, если к кабелю подвести
напряжение U
,
то
по изоляции начнет замыкаться ток,
получивший название тока утечки
(рис.11.33). Этот ток можно определить по
формуле I=UG
,
где G
- проводимость изоляции между
жилой и оболочкой кабеля.
Ранее была выведена формула ёмкости
коаксиального
кабеля
ассмотрим
конкретный пример. Изоляция коаксиального
кабеля не бывает идеальной. Практически
она обладает некоторой хотя и очень
малой удельной проводимостью
.
В связи с этим, если к кабелю подвести
напряжение U
,
то
по изоляции начнет замыкаться ток,
получивший название тока утечки
(рис.11.33). Этот ток можно определить по
формуле I=UG
,
где G
- проводимость изоляции между
жилой и оболочкой кабеля.
Ранее была выведена формула ёмкости
коаксиального
кабеля
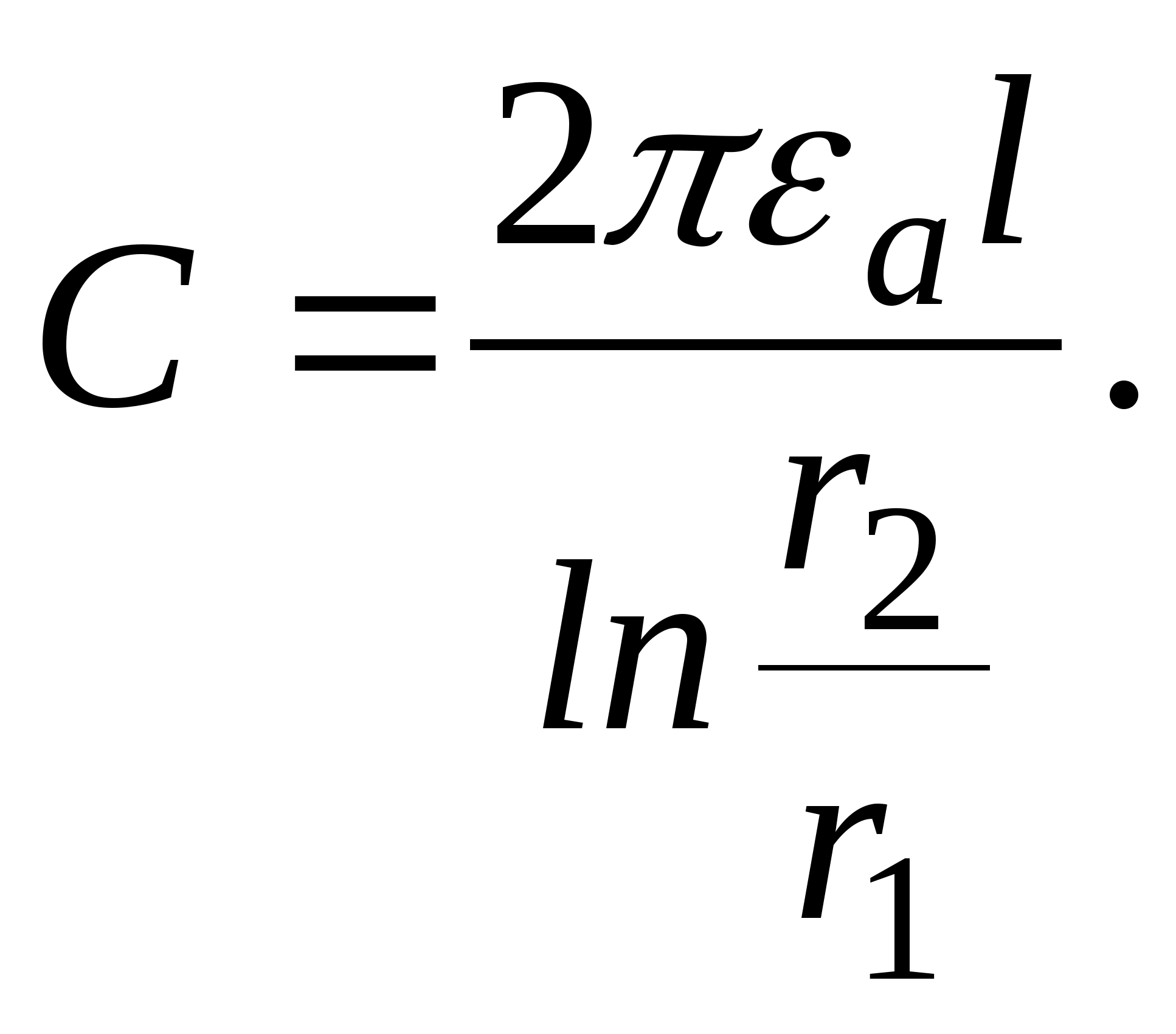 Тогда на основании аналогии
Тогда на основании аналогии
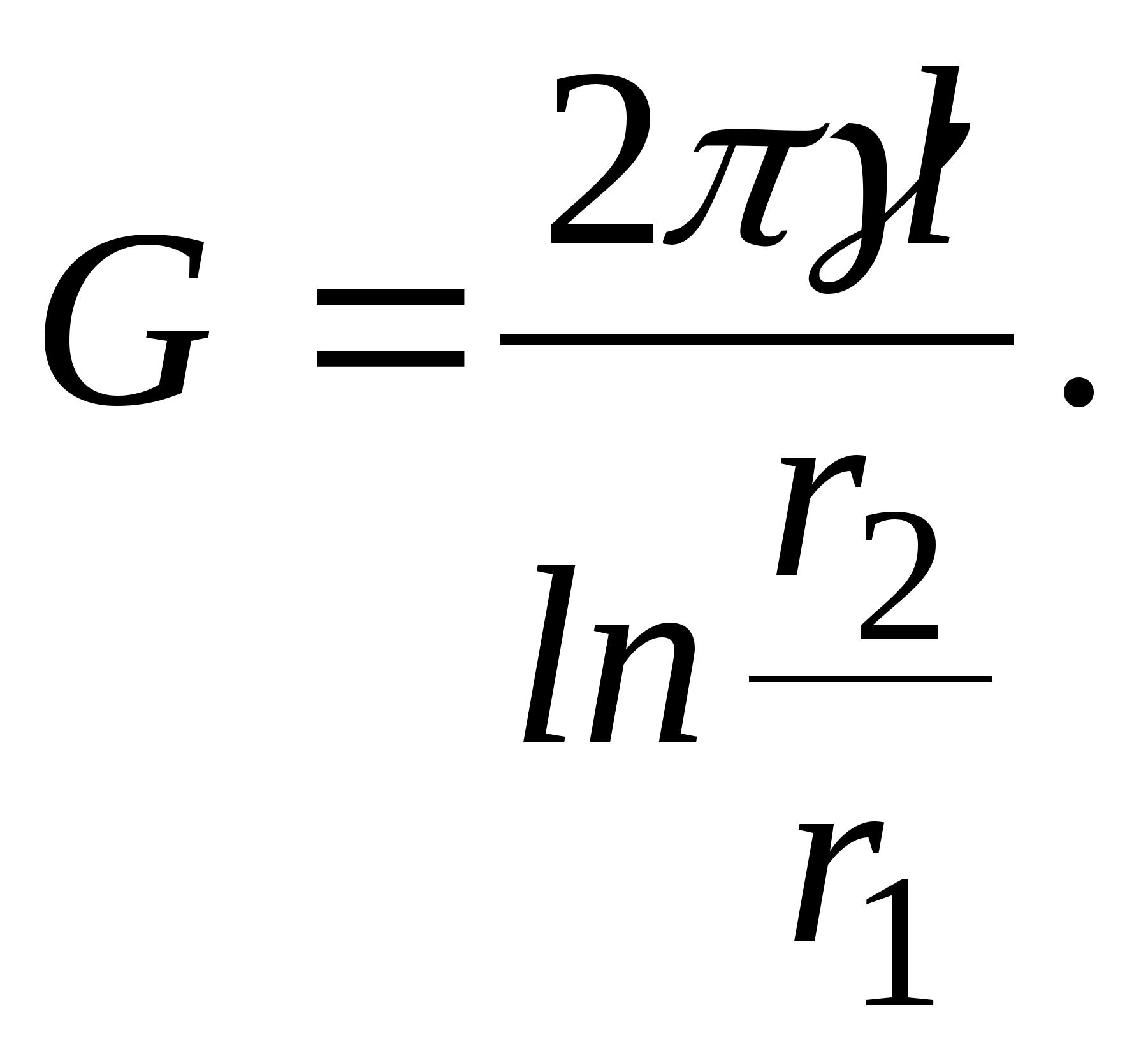
Расчет заземлителей
Для осуществления соединения каких-либо точек цепи с землей в неё зарывают металлические проводники, к которым и присоединяют соответствующие точки цепи. Система таких зарытых в землю проводников и называется заземлителем. Назначение заземлителей многообразное. Бывают рабочие заземления (трамвай), бывают защитные заземления и т. д. При коротких замыканиях (КЗ) и других авариях, а иногда и в нормальном режиме (трамвай) через заземлитель протекает ток, который растекается по земле и при этом встречает некоторое сопротивление, которое и называется сопротивлением заземлителя. Сопротивление заземлителя R з (сопротивление всей земли растеканию тока) является его первой важной характеристикой. Второй важной характеристикой является шаговое напряжение U ш – разность потенциалов между двумя точками, расположенными на поверхности земли и отстоящими друг от друга на расстоянии шага человека. Поскольку при КЗ ток, протекающий по заземлителю может иметь большие значения, то он вдоль поверхности земли может создавать вблизи от места заземления шаговое напряжение, опасное для жизни человека. Известно много случаев гибели людей от шагового напряжения. Отсюда понятна важность умения его рассчитывать. При расчете заземлителей (R з и U ш ) принимаются некоторые допущения, главными из которых являются
Перечень тестовых заданий и задач, рекомендуемых студентам для подготовки к экзаменам по разделу дисциплины Физика «Электричество и магнетизм» Тестовые задания Электростатическое поле в вакууме
ДокументШарика, если в однородном электростатическом поле шарик оказался взвешенным в глицерине. Электростатическом поле направлено вертикально вверх...
Диэлектрики в электростатическом поле. Вектор поляризации. Электрическое смещение. Теорема Гаусса для электрического смещения. 5
ДокументДиполь в однородном и неоднородном электрическом поле . 3. Диэлектрики в электростатическом поле . Вектор поляризации. 4. Электрическое... 6. Электрическая ёмкость. Конденсаторы. Энергия электростатического поля Проводники и диэлектрики. Свободные и...
Отчет по лабораторной работе №1 «исследование электростатического поля методом моделирования в проводящей среде»
ОтчетСвязь, выражающаяся соотношением: (1.1) В диэлектриках электростатическое поле характеризуется вектором электрического смещения... лать вывод о возможности моделирования электростатического поля электрическим полем в проводящей среде, если соблюдается...
На каком рисунке правильно изображена картина линий электростатического поля точечного положительного заряда?
ДокументНапряжённости электростатического поля заряда Q в точке C равен EC. Чему равен модуль напряжённости электростатического поля ... напряжённости электростатического поля заряда Q в точке С равен EС. Чему равен модуль напряжённости электростатического поля ...
Не учитывается сопротивление электродов, зарытых в землю.
В земле линии тока не уходят в бесконечность, а собираются у другого электрода. Это не учитывается поскольку мало сказывается на распределении тока вблизи рассматриваемого электрода, где плотность тока имеет наибольшее значение, и на величине соответствующего ему сопротивления заземлителя.
Шаговое напряжение у такого заземлителя отсутствует из-за далёкого расположения поверхности земли.
Шаговое напряжение где l ш - длина шага человека, которая в соответствии с Правилами Безопасности должна приниматься равной 0,8 м .
Заземлитель в виде шара, неглубоко зарытого в землю
Е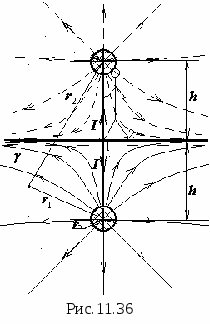 сли
заземлитель в виде шара расположен
близко от поверхности земли (рис.11.36),
то линии тока искажаются. Для учета
этого искажающего влияния поверхности
земли можно применить метод зеркальных
изображений. Линии тока у поверхности
земли должны быть к ней касательны (не
содержать нормальных составляющих).
Это условие будет выполнено, если верхнее
полупространство мысленно заполнить
проводящей средой с такой же как у земли
удельной проводимостью и поместить в
эту среду электрод, являющийся зеркальным
изображением относительно поверхности
земли действительного электрода. Ток,
подходящий к мнимому электроду должен
быть таким же по величине и знаку как и
ток действительного электрода. Поле
такого заземлителя можно определить
методом наложения от действия фактического
заземлителя и его зеркального изображения.
Потенциал любой точки поля будет
сли
заземлитель в виде шара расположен
близко от поверхности земли (рис.11.36),
то линии тока искажаются. Для учета
этого искажающего влияния поверхности
земли можно применить метод зеркальных
изображений. Линии тока у поверхности
земли должны быть к ней касательны (не
содержать нормальных составляющих).
Это условие будет выполнено, если верхнее
полупространство мысленно заполнить
проводящей средой с такой же как у земли
удельной проводимостью и поместить в
эту среду электрод, являющийся зеркальным
изображением относительно поверхности
земли действительного электрода. Ток,
подходящий к мнимому электроду должен
быть таким же по величине и знаку как и
ток действительного электрода. Поле
такого заземлителя можно определить
методом наложения от действия фактического
заземлителя и его зеркального изображения.
Потенциал любой точки поля будет
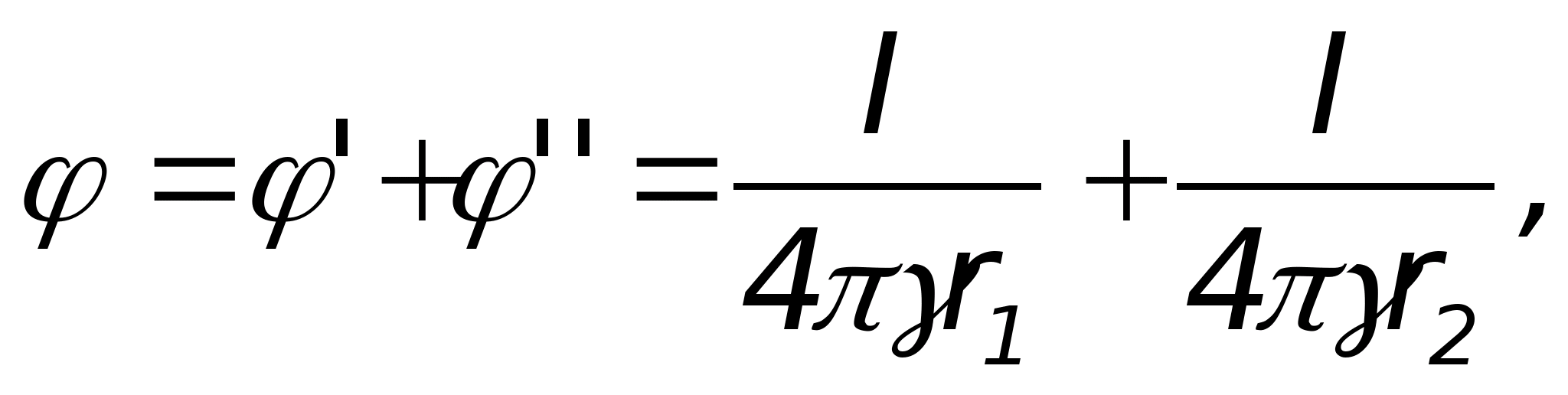 где поле
. Поле
Электростатическое
поле
создано... 13 Тема: Электростатическое
поле
. Поле
точечного заряда. Принцип суперпозиции Электростатическое
поле
создано точечным положительным...
где поле
. Поле
Электростатическое
поле
создано... 13 Тема: Электростатическое
поле
. Поле
точечного заряда. Принцип суперпозиции Электростатическое
поле
создано точечным положительным...

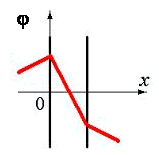
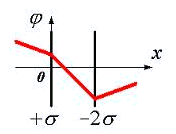
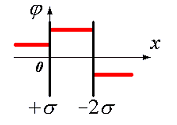
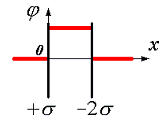
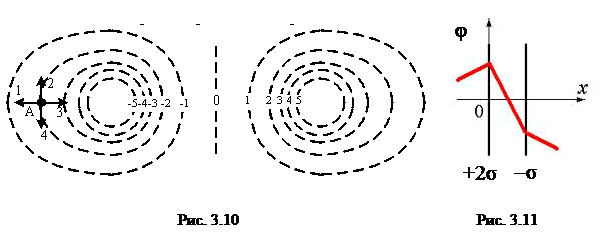
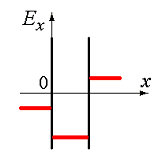 Рис. 3.12
Рис. 3.12
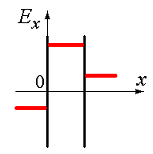 Рис. 3.13
Рис. 3.13
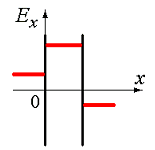 Рис. 3.14
Рис. 3.14
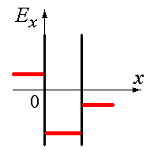 Рис. 3.15
Рис. 3.15
